자율주행 자동차 개발기 Chapter 3. 캘리브레이션 기초

참고사항

이 글은 자율주행 자동차 개발 동아리에서 활동하며 배운 내용을 바탕으로 작성되었습니다.

제목이 자율주행 자동차 개발기이지만 제가 맡은 분야(캘리브레이션)를 중심으로 정리하였습니다. 따라서 실제 자율주행 자동차 개발에 필요한 모든 내용을 다루고 있지는 않습니다.

캘리브레이션이란?

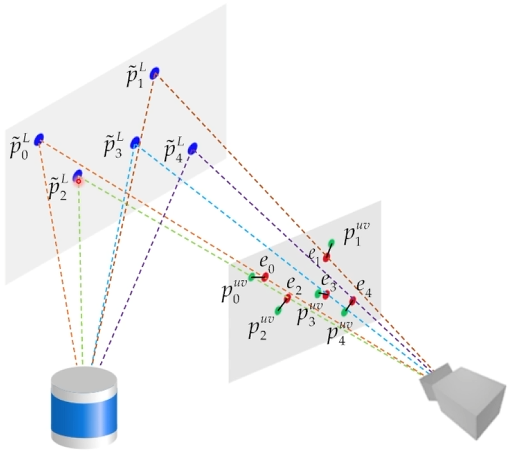
• 라이다와 카메라의 좌표계를 맞춰주는 작업
• 일반적으로 라이다의 포인트 클라우드를 카메라에 맞춤
• LiDAR → Camera: Extrinsic 사용
• Camera → Image Projection: Intrinsic 사용
• Extrinsic 변환 행렬과 Intrinsic 변환 행렬을 포인트 클라우드 좌표 행렬에 곱해 최종적으로 투영된 점을 얻을 수 있음

Extrinsic

• 카메라와 라이다 간의 위치 관계를 나타내는 \(\mathbf{R}\)(회전)과 \(\mathbf{t}\)(이동)가 필요
  • \(\mathbf{R}\): 라이다를 어느정도 회전시켜야 카메라가 바라보는 곳과 같은 곳을 바라보는지
  • \(\mathbf{t}\): 라이다가 어느정도 움직여야 카메라와 좌표가 같아지는지

  • 아래와 같은 변환 행렬을 구하는 것이 목표

    \[\mathbf{T}=\begin{bmatrix}\mathbf{R} & 0\\ \mathbf{t} & 1\end{bmatrix}\]
    • 회전 변환 행렬과 이동 변환 행렬 모두 곱해 얻을 수 있음

이동

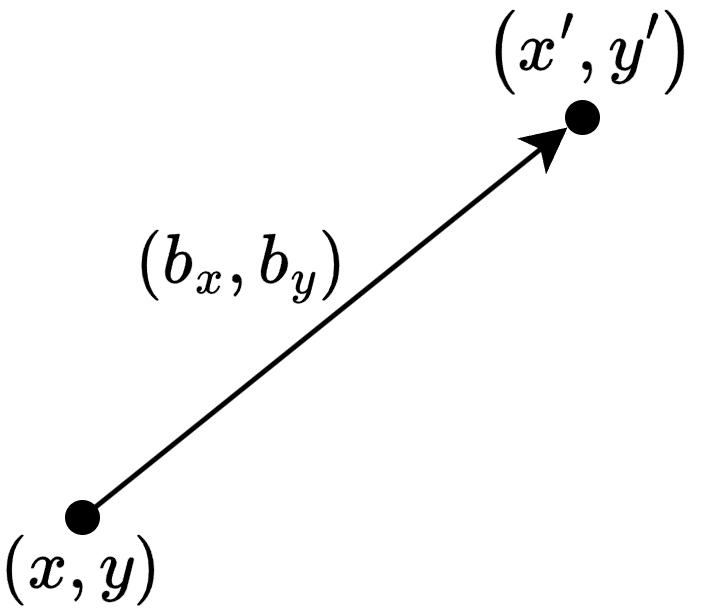
\[\begin{align*}&x^\prime=x+b_x\\&y^\prime=y+b_y\end{align*}\]

• 점 \((x, y)\)를 \(x\)방향으로 \(b_x\)만큼, \(y\)방향으로 \(b_y\)만큼 이동하는 식

\[\left[x^\prime, y^\prime, 1\right]=\left[x, y, 1\right]\left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\ b_x & b_y & 1\end{matrix}\right]\]

• 행렬을 이용해 위와 같이 나타낼 수 있음
• 3차원 공간도 비슷하게 \(b_z\)만 추가하여 4*4 변환 행렬을 이용

회전

• 3차원 공간에서의 회전은 특정 축에 대한 회전

• \(\mathbf{n}\): 회전축, 단위 벡터
• \(\mathbf{v}\): 회전시킬 벡터
• \(R_\mathbf{n}\): \(\mathbf{n}\)을 기준으로 회전시키는 함수
  • 이를 수행하는 행렬을 찾는 것이 목표
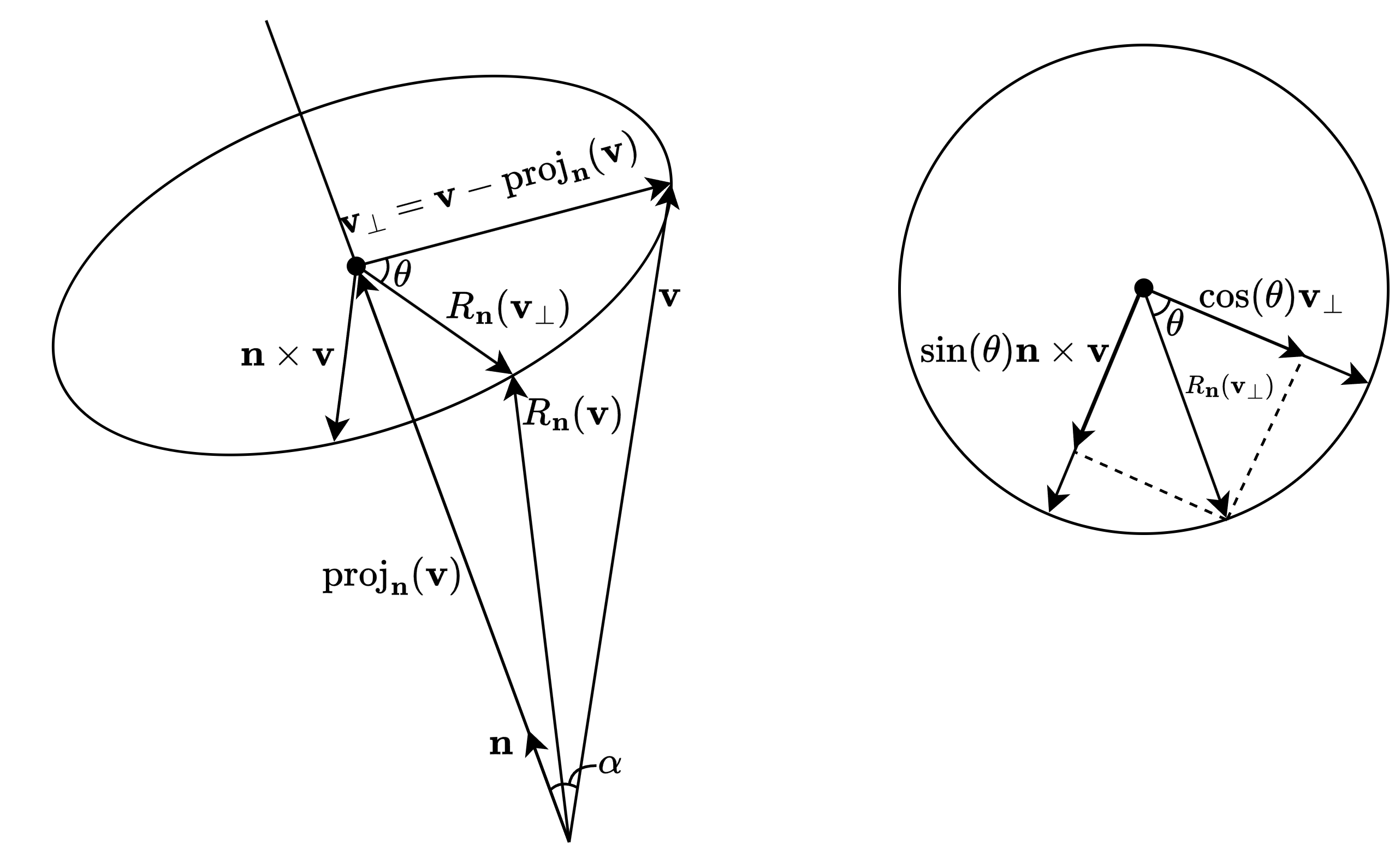
• 회전 과정
  1. $\text{proj}_\mathbf{n}(\mathbf{v})=(\mathbf{n}\cdot\mathbf{v})\mathbf{n}$
  2. \(\mathbf{v}_\bot=\mathbf{v}-\text{proj}_\mathbf{n}(\mathbf{v})\): \(\mathbf{v}\)에 수직(perpendicular)한 벡터
  3. \(\mathbf{n}\times\mathbf{v}\): \(\mathbf{v}_\bot\)​과 수직이며 길이가 같음(\(\left\Vert\mathbf{n}\times\mathbf{v}\right\Vert=\left\Vert\mathbf{n}\right\Vert\left\Vert\mathbf{v}\right\Vert\sin{\alpha}=\left\Vert\mathbf{v}_\bot\right\Vert\))
  4. \(R_\mathbf{n}(\mathbf{v}_\bot)\) 계산: \(R_\mathbf{n}(\mathbf{v}_\bot)=\cos\theta\mathbf{v}_\bot+\sin\theta(\mathbf{n}\times\mathbf{v})\)
  5. \(R_\mathbf{n}(\mathbf{v})\) 계산: \(R_\mathbf{n}(\mathbf{v})=\text{proj}_\mathbf{n}(\mathbf{v})+R_\mathbf{n}(\mathbf{v}_\bot)\)

• Rodrigues’ rotation formula(로드리게스 회전 공식)

  \[\begin{align*}R_\mathbf{n}(\mathbf{v})&=\text{proj}_\mathbf{n}(\mathbf{v})+R_\mathbf{n}(\mathbf{v}_\bot)\\&=(\mathbf{n}\cdot\mathbf{v})\mathbf{n}+\cos\theta\mathbf{v}_\bot+\sin\theta(\mathbf{n}\times\mathbf{v})\\&=(\mathbf{n}\cdot\mathbf{v})\mathbf{n}+\cos\theta(\mathbf{v}-(\mathbf{n}\cdot\mathbf{v})\mathbf{n})+\sin\theta(\mathbf{n}\times\mathbf{v})\\&=\cos\theta\mathbf{v}+(1-\cos\theta)(\mathbf{n}\cdot\mathbf{v})\mathbf{n}+\sin\theta(\mathbf{n}\times\mathbf{v})\end{align*}\]
  • 이 공식을 이용해 특정 축(\(\mathbf{n}\))에 대해 벡터 \(\mathbf{v}\)를 회전시킬 수 있음

  • 추가적으로 기저벡터를 대입해 변환 행렬을 구하는 것도 가능(기저 변환)

    \[R_\mathbf{n} = \begin{bmatrix} \leftarrow&R_\mathbf{n}(\mathbf{i})&\rightarrow\\ \leftarrow&R_\mathbf{n}(\mathbf{j})&\rightarrow\\ \leftarrow&R_\mathbf{n}(\mathbf{k})&\rightarrow \end{bmatrix} = \begin{bmatrix} c + (1-c)x^2 & (1-c)xy + sz & (1-c)xz - sy\\ (1-c)xy - sz & c + (1-c)y^2 & (1-c)yz + sx\\ (1-c)xz + sy & (1-c)yz - sx & c + (1-c)z^2 \end{bmatrix}\]

    • \(\mathbf{n}\)이 \(x\)축인 경우(\(x=1\), \(y=0\), \(z=0\))

      \[R_\mathbf{x} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & \sin\theta \\ 0 & -\sin\theta & \cos\theta \end{bmatrix}\]

    • \(\mathbf{n}\)이 \(y\)축인 경우(\(x=0\), \(y=1\), \(z=0\))

      \[R_\mathbf{y} = \begin{bmatrix}\cos\theta & 0 & -\sin\theta \\0 & 1 & 0 \\\sin\theta & 0 & \cos\theta\end{bmatrix}\]

    • \(\mathbf{n}\)이 \(z\)축인 경우(\(x=0\), \(y=0\), \(z=1\))

      \[R_\mathbf{z} = \begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

Intrinsic

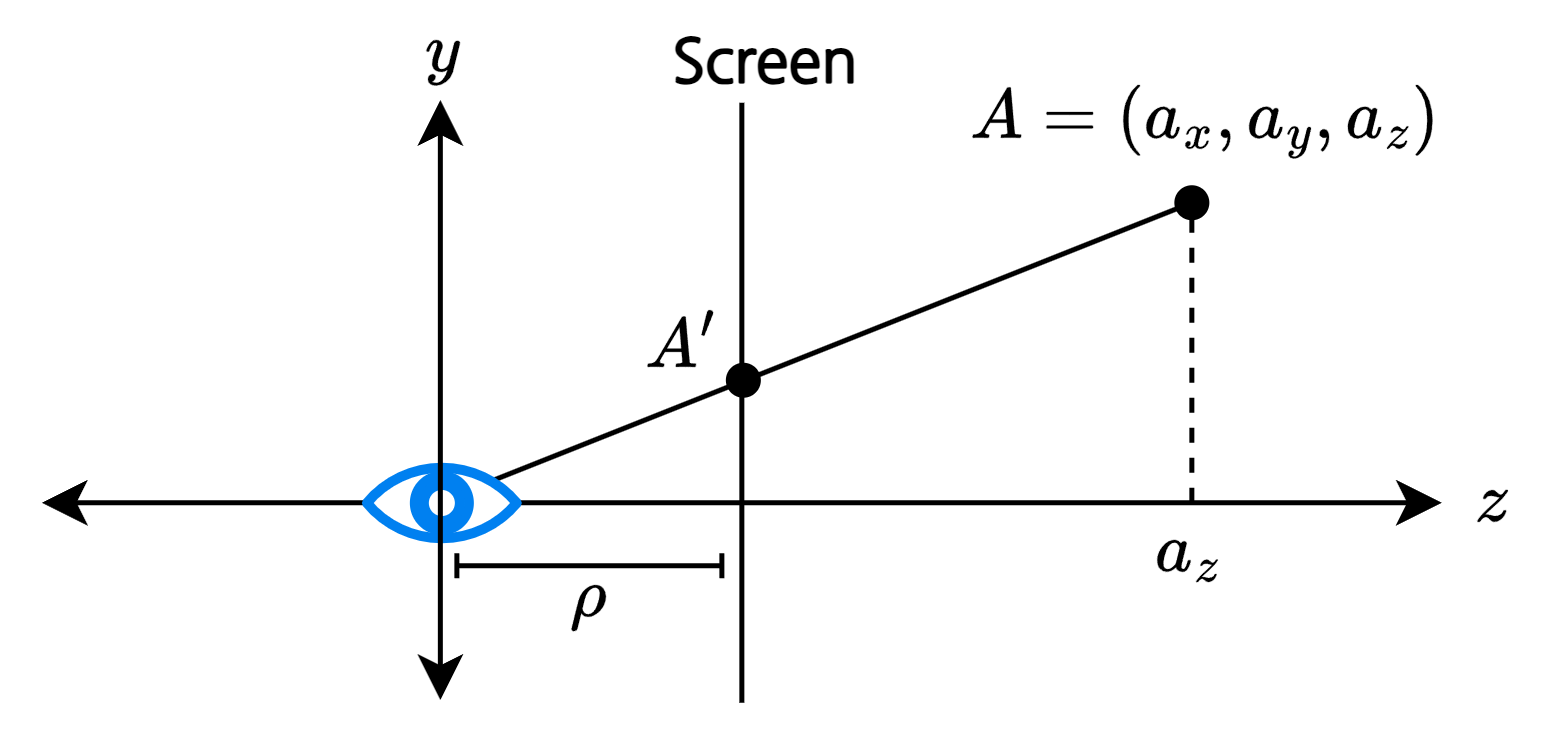
• 3차원의 점을 2차원의 이미지(스크린)에 투영

• 삼각형의 닮음을 이용해 투영된 점의 좌표를 구할 수 있음
  • \(y\) 좌표 예시
    • \(\rho: a_y^\prime = a_z : a_y\)이므로 \(a_y^\prime = \rho\frac{a_y}{a_z}\)

\[\begin{bmatrix}a_z a_x^\prime & a_z a_y^\prime & a_z^\prime\end{bmatrix}=\begin{bmatrix}a_x & a_y & a_z & 1\end{bmatrix}\begin{bmatrix}\rho & 0 & 0\\ 0 & \rho & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\end{bmatrix}=\begin{bmatrix}\rho a_x & \rho a_y & a_z\end{bmatrix}\]

• 위 변환 행렬을 곱한 결과에 \(a_z\)​를 나누면 됨