자료구조 1. 자료구조와 빅오 표기법

자료구조란?

• 효율적인 접근을 위해 자료를 보관하는 구조, 방법
• 책을 책장에 보관하는 방법
  • 아무런 규칙 없이 보관
    • 원하는 책을 찾을 때, 책장 전체를 하나하나 탐색
  • 가나다 순으로 보관
    • 원하는 책의 이름을 바탕으로 대략적인 위치를 예측 가능
  • 카테고리 별로 보관
    • 원하는 책의 카테고리에 해당하는 영역만 탐색

• 일상 생활과 자료구조 예시

  일상 생활에서의 예	자료구조
  그릇을 쌓아서 보관	스택(stack)
  대기 줄	큐(queue)
  영어 사전	딕셔너리(dictionary)
  컴퓨터 폴더 구조	트리(tree)
  지도	그래프(graph)

  • 이외에도 리스트(list), 해시(hash) 등 다양한 자료구조가 존재
• 상황에 맞는 자료구조를 선택하고 알고리즘과 조합해 프로그램을 만들 수 있음

추상 자료형(abstract data type, ADT)

• 구현 방법을 명시하지 않는 추상적 자료형
• 추상 자료형의 특징
  • 일종의 블랙박스(black box)로 사용자는 내부적으로 어떻게 동작하는지 알지 못해도 사용할 수 있음
  • 내부 구현이 변경되더라도 사용자는 이전 방식 그대로 사용할 수 있음
• TV와 비교
  • 사용자는 내부 구조(기계 회로)를 모르더라도 사용할 수 있음
  • 내부 장치(기계 부품)을 변경하더라도 이전과 같은 방식 그대로 사용할 수 있음

시간 복잡도(time complexity), 공간 복잡도(space complexity)

시간 복잡도

• 알고리즘의 연산이 대략적으로 몇 번 수행되는지를 의미
  • 일반적으로 반복문의 중첩으로 판단
• 입력의 개수(n)에 따른 연산 횟수를 \(T(n)\)처럼 함수로 나타냄
• 예)
  • \(n\)과 상관 없이 1번만 연산하는 알고리즘: \(T(n)=1\)
  • \(n\)번 연산하는 알고리즘: \(T(n)=n\)
  • \(n^2\)번 연산하는 알고리즘: \(T(n)=n^2\)

빅오 표기법(big-O notation)

• \(O(n)\)과 같이 표기
• 시간 복잡도 함수의 최고 차수만 나타내는 표기법
  • 정리: 두개의 함수 \(f(n)\), \(g(n)\)이 주어졌을 때, \(n_0\)보다 큰 모든 \(n\)에 대하여 \(f(n)\le c g(n)\)인 \(c\)와 \(n_0\)가 존재하면 \(f(n)\)의 빅오 표기법은 \(O(g(n))\)
• 예) \(T(n)=n^2 + n + 1\)
  • \(n=1\)인 경우 \(T(n)=3\)이지만, \(n=1000\)인 경우 \(T(n)=1001001\)
  • 이처럼 \(n\)이 커질수록 최고 차항의 영향력이 압도적으로 증가
  • 따라서 빅오 표기법으로 나타내면 \(O(n^2)\)​
  • 정리: \(f(n)=T(n)\)이고 \(g(n)=n^2\)일 때, \(c=2\), \(n_0=2\)라면 \(n^2+n+1 \le 2n^2\)를 만족하므로 \(O(n^2)\)

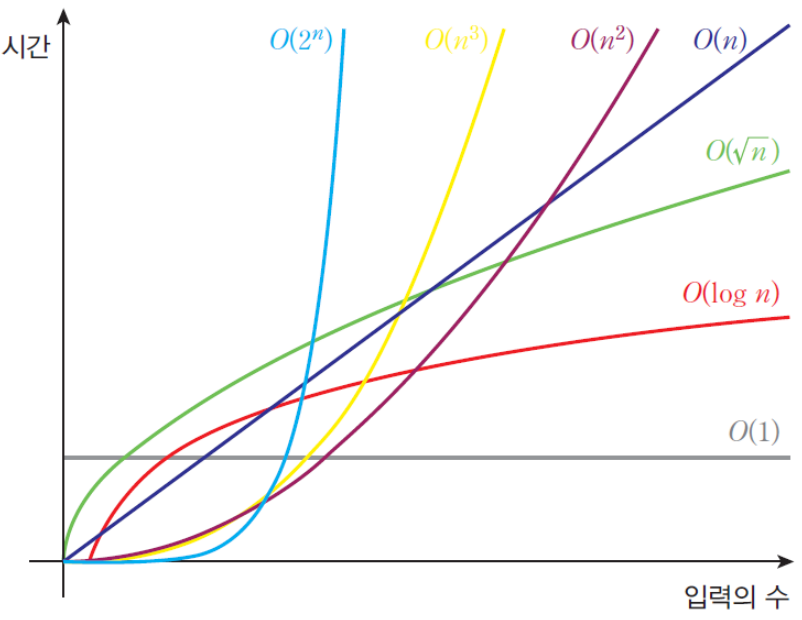
• 많이 쓰이는 빅오 표기법

  

  • \(O(1)\): 상수형(constant)
  • \(O(\log{n})\): 로그형(logarithmic)
  • \(O(n)\): 선형(linear)
  • \(O(n\log{n})\): 선형로그형(log-linear)
  • \(O(n^2)\): 2차형(quadratic)
  • \(O(n^3)\): 3차형(polynomial…)
  • \(O(2^n)\): 지수형(exponential)
  • \(O(n!)\): 팩토리얼형(factorial)
• 빅오 표기법 cheat sheet(링크)

• 3개의 표기법 중 가장 많이 쓰임

  • 최악의 경우(상한)를 나타내기 때문

빅오메가 표기법(big-omega notation)

• 빅오 표기법의 정리에 따르면 \(f(n)=2n+1\)이어도 \(O(n^2)\)이라고 할 수도 있음
  • \(n_0=1\), \(c=2\)라고 생각하면 \(2n+1 \le 2n^2\)이기 때문
• 이런 문제를 보완하기 위해 빅오메가 표기법을 사용
• 정리: 두개의 함수 \(f(n)\), \(g(n)\)이 주어졌을 때, \(n_0\)보다 큰 모든 \(n\)에 대하여 \(f(n)\ge c g(n)\)인 \(c\)와 \(n_0\)가 존재하면 \(f(n)\)의 빅오메가 표기법은 \(\Omega(g(n))\)​
  • \(f(n)=2n+1\)인 경우, \(2n+1 \ge n\)이므로 \(\Omega(n)\)
• 하한을 나타냄

빅세타 표기법(big-theta notation)

• 정리: 두개의 함수 \(f(n)\), \(g(n)\)이 주어졌을 때, \(n_0\)보다 큰 모든 \(n\)에 대하여 \(c_1 g(n)\le f(n)\le c_2 g(n)\)인 \(c_1\), \(c_2\)와 \(n_0\)가 존재하면 \(f(n)\)의 빅세타 표기법은 \(\Theta(g(n))\)​
• 3개의 표기법 중 가장 정밀