자료구조 10. 정렬

코드

• 모든 코드는 깃허브에서 확인하실 수 있습니다.

정렬

• 정보를 기준에 따라 나열하는 것
• 일반적으로 정렬시킬 대상은 레코드(recode)
  • 레코드는 필드(field)로 구성되어 있음
  • 키(key) 필드를 기준으로 레코드끼리 구별
  • 예) 학생 레코드
    • 이름 필드
    • 학번 필드(key)
    • 주소 필드
    • 연락처 필드
• 레코드의 특징에 따라 적합한 정렬 방법을 사용해야 함
  • 레코드의 수
  • key의 특징(문자, 정수, 실수 등)
• 정렬 알고리즘의 평가 기준
  • 비교 횟수
  • 이동 횟수
• 내부 정렬(internal sorting): 모든 데이터가 주기억장치에 저장된 상태에서 정렬
• 외부 정렬(external sorting): 외부기억장치에 대부분의 데이터가 있고 일부만 주기억장치에 저장된 상태에서 정렬
• 정렬 알고리즘의 안정성(stability): 동일한 key를 갖는 레코드들의 상대적인 위치가 정렬 후에도 바뀌지 않아야 함

선택 정렬(selection sort)

1. 첫번째부터 네번째까지 다음을 반복
   1. \(i\)번째 원소를 \(i \sim n\)​번째 원소 중 가장 작은 원소와 교체

• 비교 횟수: \(\frac{n(n - 1)}{2}\)

• 이동 횟수: \(3(n-1)\)

  • 교체 횟수가 \(n-1\)이므로 데이터 이동 횟수는 3배(temp 사용)

• 시간 복잡도: \(O(n^2)\)

• 안정성 만족 여부: x

• c언어

  void SelectionSort(int array[], int len)
  {
  	int temp, minIndex;
  	for (int i = 0; i < len - 1; ++i)
  	{
  		minIndex = i;
  		for (int j = i + 1; j < len; ++j)
  		{
  			if (array[j] < array[minIndex])
  			{
  				minIndex = j;
  			}
  		}
    
  		temp = array[i];
  		array[i] = array[minIndex];
  		array[minIndex] = temp;
  	}
  }
  

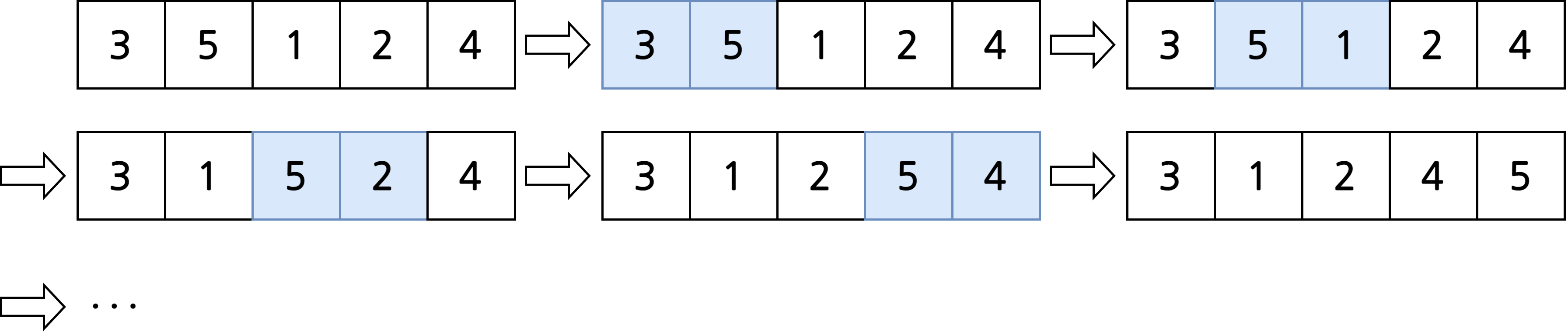
삽입 정렬(insertion sort)

1. 두번째부터 마지막까지 차례로 key로 설정하고 다음을 반복
   1. key 이전의 원소들과 비교하여 key를 적절한 위치로 이동

• 비교 횟수

  • 최선의 경우: \(n-1\)
  • 최악의 경우: \(\frac{n(n-1)}{2}\)

• 이동 횟수

  • 최선의 경우: \(2(n-1)\)​
    • key로 이동, array[j + 1]로 이동
  • 최악의 경우: \(\frac{n(n-1)}{2} + 2(n-1)\)

• 시간 복잡도: \(O(n^2)\)

• 안정성 만족 여부: o

• c언어

  void InsertionSort(int array[], int len)
  {
  	int i, j, key;
    
  	for (i = 1; i < len; ++i)
  	{
  		key = array[i];
  		for (j = i - 1; j >= 0; --j)
  		{
  			if (array[j] > key)
  			{
  				array[j + 1] = array[j];
  			}
  			else
  			{
  				break;
  			}
  		}
  		array[j + 1] = key;
  	}
  }
  

버블 정렬(bubble sort)

1. \(n - 1\)번째부터 두번째까지 다음을 반복
   1. 첫번째부터 \(i\)번째까지 다음을 반복
      1. \(j\)번째와 \(j + 1\)번째 요소를 비교하여 \(j\)번째 요소가 더 크다면 서로 교체

• 비교 횟수: \(\frac{n(n-1)}{2}\)

• 이동 횟수

  • 최선의 경우: \(0\)
  • 최악의 경우: \(3\frac{n(n-1)}{2}\)

• 시간 복잡도: \(O(n^2)\)​

• 안정성 만족 여부: o

• c언어

  void BubbleSort(int array[], int len)
  {
  	int temp;
  	for (int i = len - 1; i > 0; --i)
  	{
  		for (int j = 0; j < i; ++j)
  		{
  			if (array[j] > array[j + 1])
  			{
  				temp = array[j];
  				array[j] = array[j + 1];
  				array[j + 1] = temp;
  			}
  		}
  	}
  }
  

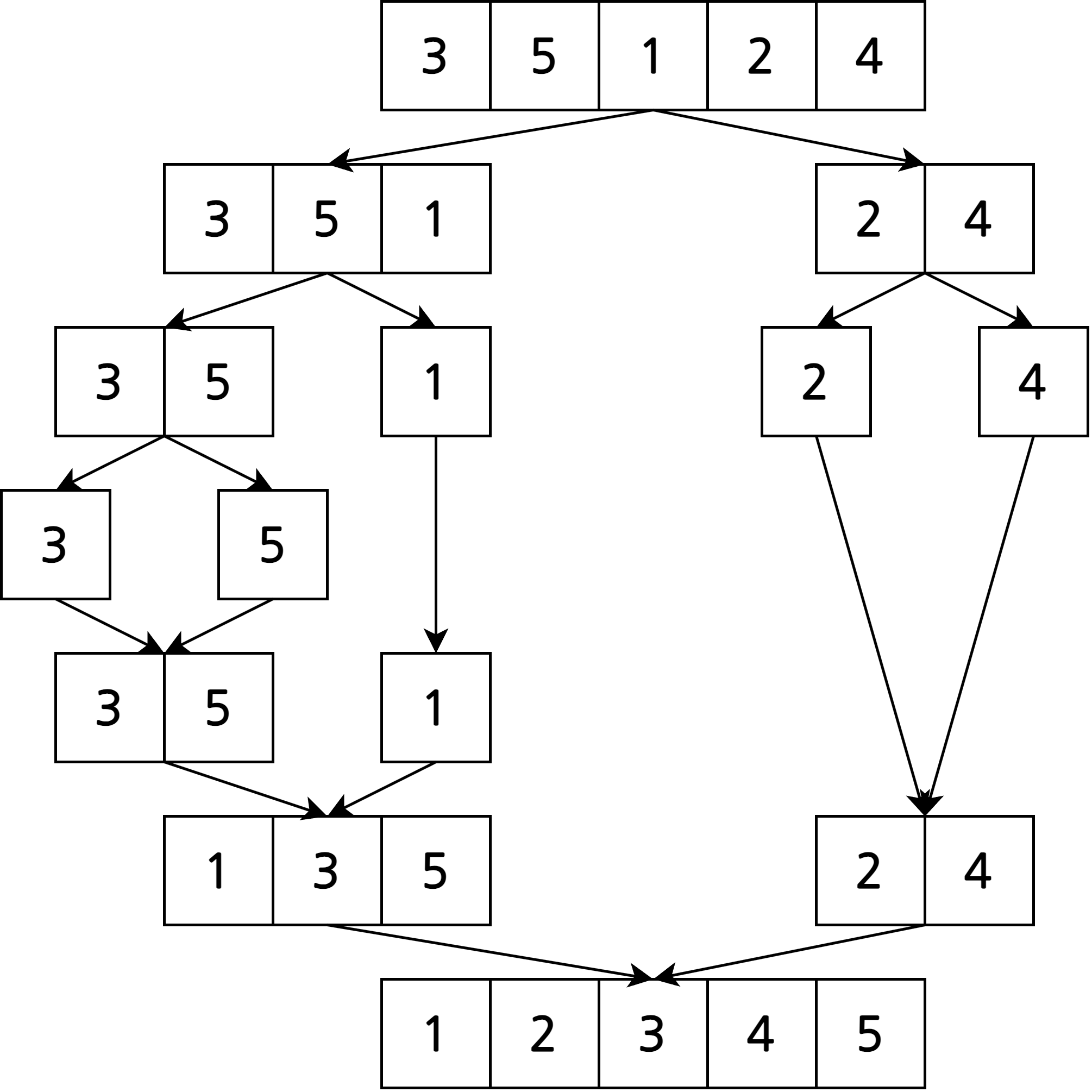
합병 정렬(merge sort)

1. 배열을 두 개의 균등한 크기로 분할하여 부분 배열을 정렬
2. 정렬된 두 개의 부분 배열을 합하여 전체 배열을 정렬

• 비교 횟수: \(n\log n\)

• 이동 횟수: \(2n\log n\)

• 시간 복잡도: \(O(n\log n)\)

• 안정성 만족 여부: o

• c언어

  void MergeRecursive(int array[], int temp[], int left, int right)
  {
  	if (left == right)
  	{
  		return;
  	}
  	int mid = (left + right) / 2;
  	int i, j, k;
    
  	MergeRecursive(array, temp, left, mid);
  	MergeRecursive(array, temp, mid + 1, right);
    
  	i = left;
  	j = mid + 1;
  	k = left;
  	while (i <= mid && j <= right)
  	{
  		if (array[i] <= array[j])
  		{
  			temp[k++] = array[i++];
  		}
  		else
  		{
  			temp[k++] = array[j++];
  		}
  	}
    
  	while (i <= mid)
  	{
  		temp[k++] = array[i++];
  	}
    
  	while (j <= right)
  	{
  		temp[k++] = array[j++];
  	}
    
  	for (i = left; i <= right; ++i)
  	{
  		array[i] = temp[i];
  	}
  }
    
  void MergeSort(int array[], int left, int right)
  {
  	int* temp = (int*)malloc(sizeof(int) * (right - left + 1));
    
  	MergeRecursive(array, temp, left, right);
    
  	free(temp);
  }
  

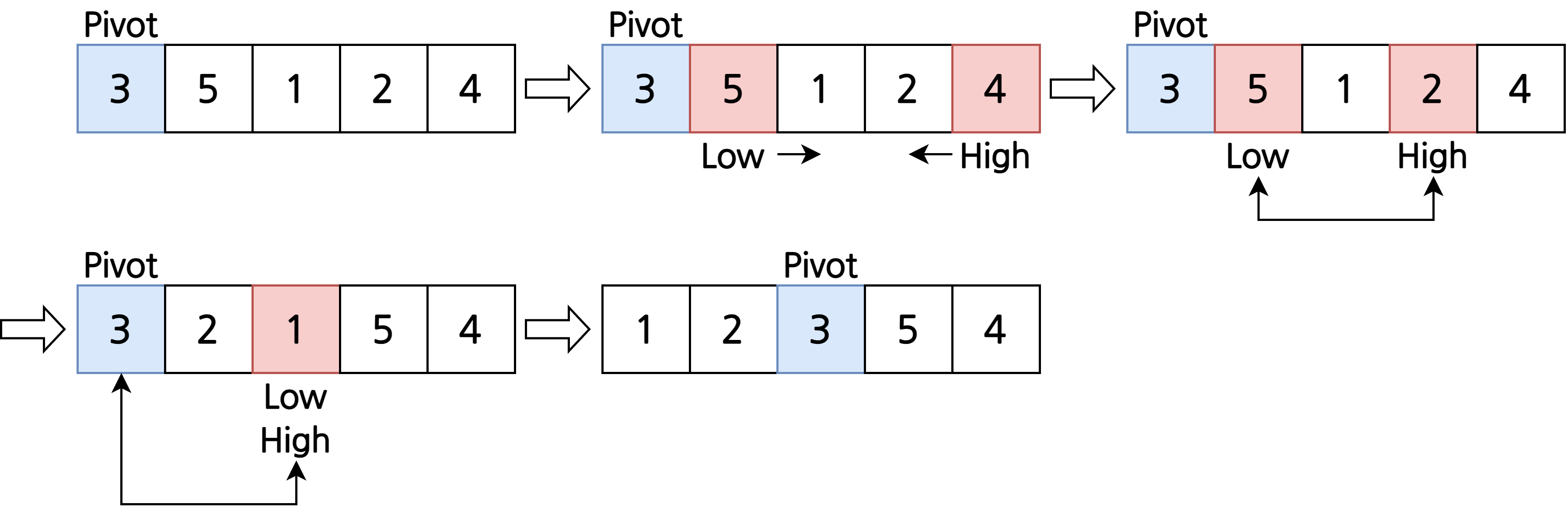
퀵 정렬(quick sort)

1. pivot을 기준으로 왼쪽은 pivot보다 큰 값, 오른쪽은 pivot보다 작은 값을 탐색
2. 찾은 두 값을 교환
3. low와 high가 엇갈리기 전까지 1번으로 돌아가 반복
4. high와 pivot을 교체
5. 부분 배열에 대해 재귀적으로 반복

• 비교 횟수: \(n\log n\)

• 시간 복잡도: \(O(n \log n)\)

• 안정성 만족 여부: o

• c언어

  void QuickSort(int array[], int left, int right)
  {
      if (left >= right)
      {
          return;
      }
    
      int pivot = array[left];
      int low = left + 1;
      int high = right;
      int temp;
    
      while (low <= high)
      {
          while (low <= high && array[low] <= pivot)
          {
              ++low;
          }
    
          while (low <= high && array[high] >= pivot)
          {
              --high;
          }
    
          if (low < high)
          {
              temp = array[low];
              array[low] = array[high];
              array[high] = temp;
          }
      }
    
      array[left] = array[high];
      array[high] = pivot;
    
      QuickSort(array, left, high - 1);
      QuickSort(array, high + 1, right);
  }