자료구조 3. 배열

코드

• 모든 코드는 깃허브에서 확인하실 수 있습니다.

배열(array)

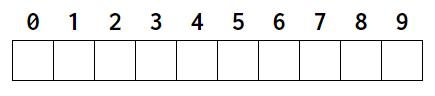
• 데이터를 연속적으로 저장하는 자료구조
• index에 value이 대응됨
  • index는 0부터 시작
    • 첫 번째 요소의 시작점과 배열의 시작점이 같기 때문
    • 배열의 주소 = 첫 번째 요소의 주소 + 0
  • arr[3]처럼 index를 통해 value에 접근할 수 있음
• c언어
  • type arrayName[length] = { init };

2차원, 3차원 배열

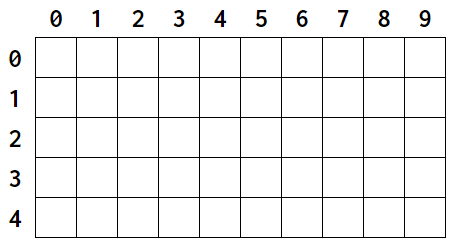
• 2차원 배열

  

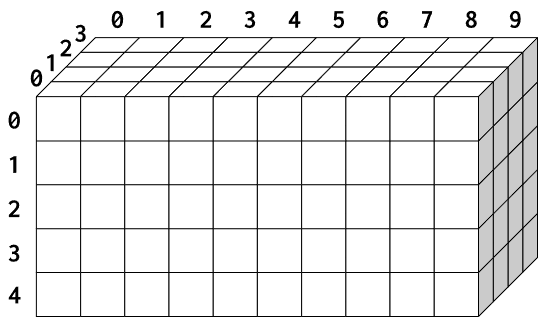
• 3차원 배열

  

• c언어

  • 2d array: type arrayName[row][col] = { {}, {}, ... };

  • 3d array: type arrayName[depth][row][col] = { { {}, {}, ...}, { {}, {}, ...}, ... };

• 메모리에는 1차원 배열처럼 일렬로 저장됨

  • 주로 row-major 방향으로 저장
    • [i][j] = i * col(width) + j

구조체

• 다양한 자료형을 모아놓은 구조

• 관리의 용이성을 위해 사용

• 예)

  • 좌표를 표현하는 구조체: (x, y, z)
  • 이름과 학번을 저장하는 구조체: (name, id)

• c언어

  • 정의

    struct StructName
    {
        type name;
        ...
    };
    

    • typedef과 함께 이용하면 편리

      typedef struct 
      {
          type name;
          ...
      } StructName;
      

  • 구조체 선언

    • struct StructName varName = { init };
    • typedef를 사용한 경우: StructName varName = { init };
    • StructName varName = { .name="name", ... };처럼 멤버 변수를 초기화할 수 있음

다항식(polynomial)

방법 1

• 모든 계수를 배열에 저장
  • 최고 차항의 계수를 0번째 index에 저장
  • 최고 차항의 차수를 따로 저장
• 예)
  • \(ax^2+bx+c\): [a, b, c], degree = 2
  • \(ax^5+bx^4+cx\): [a, b, 0, 0, c, 0], degree = 5
• c언어

  • 다항식 구조체 정의

    typedef struct
    {
        int degree;
        float coef[MAX_DEGREE];
    } Polynomial;
    

    • degree: 다항식의 최고 차항의 차수
    • coef: 다항식 계수 배열

  • 다항식 덧셈

    Polynomial AddPolynomial(Polynomial a, Polynomial b)
    {
        // 1
        if (a.degree < b.degree)
        {
            Polynomial temp = a;
            a = b;
            b = temp;
        }
        	
        // 2
        int highestDiff = a.degree - b.degree;
        for (int i = 0; i <= b.degree; ++i)
        {
            a.coef[i + highestDiff] += b.coef[i];
        }
        
        return a;
    }
    

    1. a의 최고 차항의 차수가 b의 최고 차항의 차수보다 작다면 서로 swap
    2. a에 b를 덧셈
       • b의 최고 차항의 차수보다 차수가 큰 a의 항은 생각할 필요가 없음
       • 따라서 b를 기준으로 반복
       • highestDiff: b의 최고 차항의 계수가 a에서는 a.degree - b.degree번째이므로 i + highestDiff를 통해 위치 보정

  • 다항식 출력

    void PrintPolynomial(Polynomial poly)
    {
        printf("%gx^%d", poly.coef[0], poly.degree);
        for (int i = 1; i < poly.degree; ++i)
        {
            if (poly.coef[i] == 0)
            {
                continue;
            }
            printf("%+gx^%d", poly.coef[i], poly.degree - i);
        }
        printf("%+g\n", poly.coef[poly.degree]);
    }
    

    • %g: 소수점 이하 0 제거
    • %+g: 부호 출력
    • 최고 차항의 계수는 +를 보여줄 필요가 없으므로 먼저 출력
    • 계수가 0일 경우 출력할 필요가 없으므로 반복문 내에서 검사
    • 상수항은 x를 출력할 필요가 없으므로 반복문 밖에서 출력

방법 2

• 공간을 절약하기 위해 계수가 0이 아닌 항만 저장
  • (계수, 차수) 형식의 구조체를 배열에 저장
  • (계수, 차수)들은 차수에 따른 내림차순으로 정렬되어 있다고 가정
• 예)
  • \(ax^2+bx+c\): { {a, 2}, {b, 1}, {c, 0} }
  • \(ax^5+bx^4+cx\): { {a, 5}, {b, 4}, {c, 1} }

• c언어

  • 다항식 구조체 정의

    typedef struct
    {
    	float coef;
    	int exponent;
    } Term;
        
    typedef struct
    {
    	Term terms[MAX_TERMS];
    	int availIndex;
    } Polynomial;
    

    • 다항식 구조체(Polynomial)에서 항 구조체(Term) 배열을 사용
    • availIndex: 마지막 유효한 항의 index

  • 항 추가

    int AttachTerm(Polynomial* target, Term term)
    {
        if (target->availIndex >= MAX_TERMS)
        {
            return 0;
        }
        
        target->terms[target->availIndex] = term;
        ++(target->availIndex);
        
        return 1;
    }
    

    • 항 개수가 최대 항 개수를 이상이면 실패(0) 반환
    • 마지막 항 뒤에 새로운 항 추가

  • 다항식 덧셈

    Polynomial AddPolynomial(Polynomial a, Polynomial b)
    {
        Polynomial res = { .availIndex = 0 };
        int aIndex = 0;
        int bIndex = 0;
        
        while (aIndex < a.availIndex && bIndex < b.availIndex)
        {
            float aExpon = a.terms[aIndex].exponent;
            float bExpon = b.terms[bIndex].exponent;
        
            if (aExpon > bExpon)
            {
                AttachTerm(&res, a.terms[aIndex]);
                ++aIndex;
            }
            else if (aExpon < bExpon)
            {
                AttachTerm(&res, b.terms[bIndex]);
                ++bIndex;
            }
            else
            {
                AttachTerm(&res, (Term){ a.terms[aIndex].coef + b.terms[bIndex].coef, a.terms[aIndex].exponent });
        
                ++aIndex;
                ++bIndex;
            }
        }
        
        for (int i = aIndex; i < a.availIndex; ++i)
        {
            AttachTerm(&res, a.terms[i]);
        }
        for (int i = bIndex; i < b.availIndex; ++i)
        {
            AttachTerm(&res, b.terms[i]);
        }
        
        return res;
    }
    

    • aIndex와 bIndex를 이용해 처음부터 탐색, 만약 둘 중 하나라도 모든 항을 탐색하면 탐색 종료
    • aIndex에 해당하는 항의 차수와 bIndex에 해당하는 항의 차수를 비교해 더 큰 항을 결과에 추가, 만약 같다면 두 항의 계수를 더해 추가
    • 탐색을 종료하면 추가되지 못한 다항식의 항을 마저 추가

  • 다항식 출력

    void PrintPolynomial(Polynomial poly)
    {
        printf("%gx^%d", poly.terms[0].coef, poly.terms[0].exponent);
        
        for (int i = 1; i < poly.availIndex - 1; ++i)
        {
            printf("%+gx^%d", poly.terms[i].coef, poly.terms[i].exponent);
        }
        
        if (poly.terms[poly.availIndex - 1].exponent == 0)
        {
            printf("%+g\n", poly.terms[poly.availIndex - 1].coef);
        }
        else
        {
            printf("%+gx^%d\n", poly.terms[poly.availIndex - 1].coef, poly.terms[poly.availIndex - 1].exponent);
        }
    }
    

    • 방법1과 유사
    • 마지막 항이 상수항일 경우 x를 제외하고 출력