자료구조 4. 스택

코드

• 모든 코드는 깃허브에서 확인하실 수 있습니다.

스택(stack)

• 데이터를 쌓는 형태의 자료구조
  • 데이터를 추가할 때는 맨 위에만 추가 가능(push)
  • 데이터를 삭제할 때는 맨 위에만 삭제 가능(pop)
  • 이러한 구조를 LIFO(Last In First Out)라고 부름

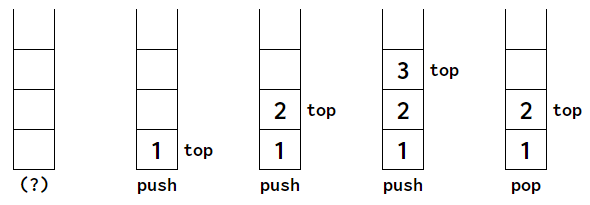
• 위 그림처럼 top을 이용해 데이터의 상단을 표시

  • push를 한다면 top이 1 증가
  • pop을 한다면 top이 1 감소

• stack의 기능

  • isFull: 스택이 포화상태인지 확인
  • isEmpty: 스택이 비어있는지 확인
  • push: 스택의 맨 위에 새로운 값을 추가
    • isFull로 포화상태가 아닌것을 확인 후 값 추가
  • pop: 스택의 맨 위의 값을 제거하고 반환
    • isEmpty로 스택이 비어있지 않았다는 것을 확인 후 값 삭제
  • peek: 스택의 맨 위의 값을 확인
    • isEmpty로 스택이 비어있지 않았다는 것을 확인 후 값 확인

• c언어

  • 스택 구조체 정의

    typedef struct
    {
    	int elements[MAX_STACK_SIZE];
    	int top;
    } Stack;
    

  • IsFull

    int IsFull(const Stack* stack)
    {
    	return (stack->top == sizeof(stack->elements) - 1);
    }
    

  • IsEmpty

    int IsEmpty(const Stack* stack)
    {
    	return (stack->top == -1);
    }
    

  • Push

    void Push(Stack* stack, int value)
    {
    	assert(!IsFull(stack));
        
    	++(stack->top);
    	stack->elements[stack->top] = value;
    }
    

    • assert를 이용해 스택이 포화상태라면 에러 발생

  • Pop

    int Pop(Stack* stack)
    {
    	assert(!IsEmpty(stack));
        
    	return stack->elements[stack->top--];
    }
    

    • 데이터를 삭제하지 않고, top을 감소시키는 것만으로 삭제한 것과 비슷한 효과를 냄

  • Peek

    int Peek(const Stack* stack)
    {
    	assert(!IsEmpty(stack));
        
    	return stack->elements[stack->top];
    }
    

  • 이 방법 외에 realloc을 이용해 동적으로 스택의 크기를 늘리는 방법도 존재

괄호 검사 문제(valid parentheses problem)

• 괄호가 쌍이 되는지 검사하는 문제

  • 예) {arr[Func(a)-(i + j)]}

• 조건

  1. 왼쪽 괄호와 오른쪽 괄호의 개수가 같아야 함
  2. 같은 종류의 괄호에서 왼쪽 괄호가 오른쪽 괄호보다 먼저 나와야 함
  3. 서로 다른 종류의 괄호 쌍이 교차되면 안됨

• 풀이법

  • 문자열의 왼쪽부터 검사
    • 왼쪽 괄호면 스택에 push
    • 오른쪽 괄호면 스택을 pop한 후 같은 종류의 괄호인지 검사
      • 같은 종류의 괄호면 continue
      • 다른 종류의 괄호면 false 반환
    • 그 외 일반 문자면 continue
  • 검사가 끝나면 true 반환

• c언어

  int CheckParanthesis(char* str)
  {
  	Stack paranthesisStack = { .top = -1 };
    
  	while (*str != '\0')
  	{
  		switch (*str)
  		{
  		case '[':
  		case '{':
  		case '(':
  			Push(&paranthesisStack, *str);
  			break;
    
  		case ']':
  			if (IsEmpty(&paranthesisStack) || Pop(&paranthesisStack) != '[')
  			{
  				return 0;
  			}
  			break;
  		case '}':
  			if (IsEmpty(&paranthesisStack) || Pop(&paranthesisStack) != '{')
  			{
  				return 0;
  			}
  			break;
  		case ')':
  			if (IsEmpty(&paranthesisStack) || Pop(&paranthesisStack) != '(')
  			{
  				return 0;
  			}
  			break;
  		}
    
  		++str;
  	}
    
  	return 1;
  }
  

후위 표기법 계산

• 컴파일러는 사람이 작성한 수식(중위 표기법)을 후위 표기법으로 변환하여 계산

  • 중위 표기법: 2+3*4
  • 후위 표기법: 234*+
  • 스택을 이용하여 중위 표기법을 후위 표기법으로 변환할 수 있음
  • 마찬가지로 스택을 이용하여 후위 표기법을 계산할 수 있음

• 중위 표기법 -> 후위 표기법

  • 중위 표기법의 왼쪽부터 검사
    • 숫자면 결과 문자열에 append
    • *, /면 스택에 push
    • +, -면 스택의 맨 위에 *, /가 있는지 검사
      • 있다면 pop하여 결과 문자열에 append
      • *, / 유무 상관 없이 스택에 push
    • (면 스택에 push
    • )면 스택을 pop하여 (가 나올때까지 pop한 결과를 결과 문자열에 append
  • 스택이 빌 때까지 pop하여 결과 문자열에 append

• 후위 표기법 계산

  • 후위 표기법의 왼쪽부터 검사
    • 숫자면 스택에 push
    • *, /, +, -면 스택에서 2번 pop하여 계산 후 결과를 스택에 push
      • (나중에 pop된 숫자) 연산 (먼저 pop된 숫자)
  • 스택을 pop하여 반환

• c언어

  • 중위 표기법 -> 후위 표기법

    int ConvertInfixToPostfix(char* expression, char* result)
    {
    	if (!CheckParanthesis(expression))
    	{
    		return 0;
    	}
        
    	Stack operatorStack = { .top = -1 };
    	char topOperator;
        
    	while (*expression != '\0')
    	{
    		switch (*expression)
    		{
    		case '*':
    		case '/':
    		case '(':
    			Push(&operatorStack, *expression);
    			break;
    		case '+':
    		case '-':
    			if (!IsEmpty(&operatorStack))
    			{
    				topOperator = Peek(&operatorStack);
    				if (topOperator == '*' || topOperator == '/')
    				{
    					*result = Pop(&operatorStack);
    					++result;
    				}
    			}
    			Push(&operatorStack, *expression);
    			break;
    		case ')':
    			while ((topOperator = Pop(&operatorStack)) != '(')
    			{
    				*result = topOperator;
    				++result;
    			}
    				break;
    		default:
    			*result = *expression;
    			++result;
    			break;
    		}
        
    		++expression;
    	}
        
    	while (!IsEmpty(&operatorStack))
    	{
    		*result = Pop(&operatorStack);
    		++result;
    	}
        
    	*result = '\0';
        
    	return 1;
    }
    

  • 후위 표기법 계산

    int EvaluatePostfix(char* expression)
    {
    	Stack stack = { .top = -1 };
    	int firstNum, secondNum, temp;
        
    	while (*expression != '\0')
    	{
    		switch (*expression)
    		{
    		case '*':
    			secondNum = Pop(&stack);
    			firstNum = Pop(&stack);
    			temp = firstNum * secondNum;
    			Push(&stack, temp);
    			break;
    		case '/':
    			secondNum = Pop(&stack);
    			firstNum = Pop(&stack);
    			temp = firstNum / secondNum;
    			Push(&stack, temp);
    			break;
    		case '+':
    			secondNum = Pop(&stack);
    			firstNum = Pop(&stack);
    			temp = firstNum + secondNum;
    			Push(&stack, temp);
    			break;
    		case '-':
    			secondNum = Pop(&stack);
    			firstNum = Pop(&stack);
    			temp = firstNum - secondNum;
    			Push(&stack, temp);
    			break;
    		default:
    			Push(&stack, *expression - '0');
    			break;
    		}
        
    		++expression;
    	}
        
    	return Pop(&stack);
    }