자료구조 8. 우선순위 큐

코드

• 모든 코드는 깃허브에서 확인하실 수 있습니다.

우선순위 큐(priority queue)

• 우선순위를 가진 항목들을 저장하는 큐

• FIFO가 아닌 우선순위가 높은 데이터가 먼저 나감

• 우선순위 큐의 기능
  • create: 우선순위 큐 생성
  • is_empty: 우선순위 큐가 비어있는지 검사
  • is_full: 우선순위 큐가 포화 상태인지 검사
  • insert: 우선순위 큐에 요소 추가
  • delete: 우선순위 큐에서 우선순위가 가장 높은 요소 삭제하고 반환
  • find: 우선순위가 가장 높은 요소 반환
• 우선순위 큐 표현법
  • 배열 표현법
  • 연결리스트 표현법
  • 힙(heap) 표현법

• 우선순위 큐가 사용되는 곳

  • 머신 스케줄링(LPT, Longest Processing Time first)

    • \(n\)개의 작업과 \(m\)​개의 스레드가 있을 때 작업을 스레드에 분배하는 방법

    

    1. 우선순위 큐(시간이 긴 작업이 우선)에 모든 작업을 차례로 삽입
    2. 다음 과정을 우선순위 큐의 원소가 없을 때까지 실행
       1. \(1\)번 스레드부터 \(m\)​번 스레드까지 차례로 우선순위 큐에서 작업을 배정
       2. \(m\)번 스레드부터 \(1\)번 스레드까지 차례로 우선순위 큐에서 작업을 배정

우선순위 큐 표현법

배열 표현법

• 순서 없는 배열 표현법
  • insert 할 때, 단순히 배열에 요소를 저장
  • delete 할 때, 우선순위가 가장 높은 요소를 찾아 반환
  • 시간 복잡도
    • insert: \(O(1)\)
    • delete: \(O(n)\)
• 정렬된 배열 표현법
  • insert 할 때, 요소를 정렬하여 저장
  • delete 할 때, 맨 앞 원소 반환
  • 시간 복잡도
    • insert: \(O(n)\)
    • delete: \(O(1)\)

연결리스트 표현법

• 순서 없는 연결리스트 표현법
  • insert 할 때, 단순히 연결리스트에 요소를 저장
  • delete 할 때, 우선순위가 가장 높은 요소를 찾아 반환
  • 시간 복잡도
    • insert: \(O(1)\)
    • delete: \(O(n)\)
• 정렬된 연결리스트 표현법
  • insert 할 때, 요소를 정렬하여 저장
  • delete 할 때, 맨 앞 원소 반환
  • 시간 복잡도
    • insert: \(O(n)\)
    • delete: \(O(1)\)

힙 표현법

• 힙: 완전 이진 트리의 한 종류

  • 최대 힙(max heap): 부모 노드의 값이 자식 노드의 값보다 크거나 같은 완전 이진 트리

  • 최소 힙(min heap): 부모 노드의 값이 자식 노드의 값보다 작거자 같은 완전 이진 트리

  • 힙은 완전 이진 트리이므로 배열을 이용해 구현

    • 각 노드의 번호를 배열의 인덱스로 생각

    • 왼쪽 자식의 인덱스: [부모의 인덱스] * 2

    • 오른쪽 자식의 인덱스: [부모의 인덱스] * 2 + 1

    • 부모의 인덱스: [자식의 인덱스] / 2

    • c언어

      typedef struct
      {
      	int heap[MAX_HEAP_SIZE];
      	int heapSize;
      } Heap;
      

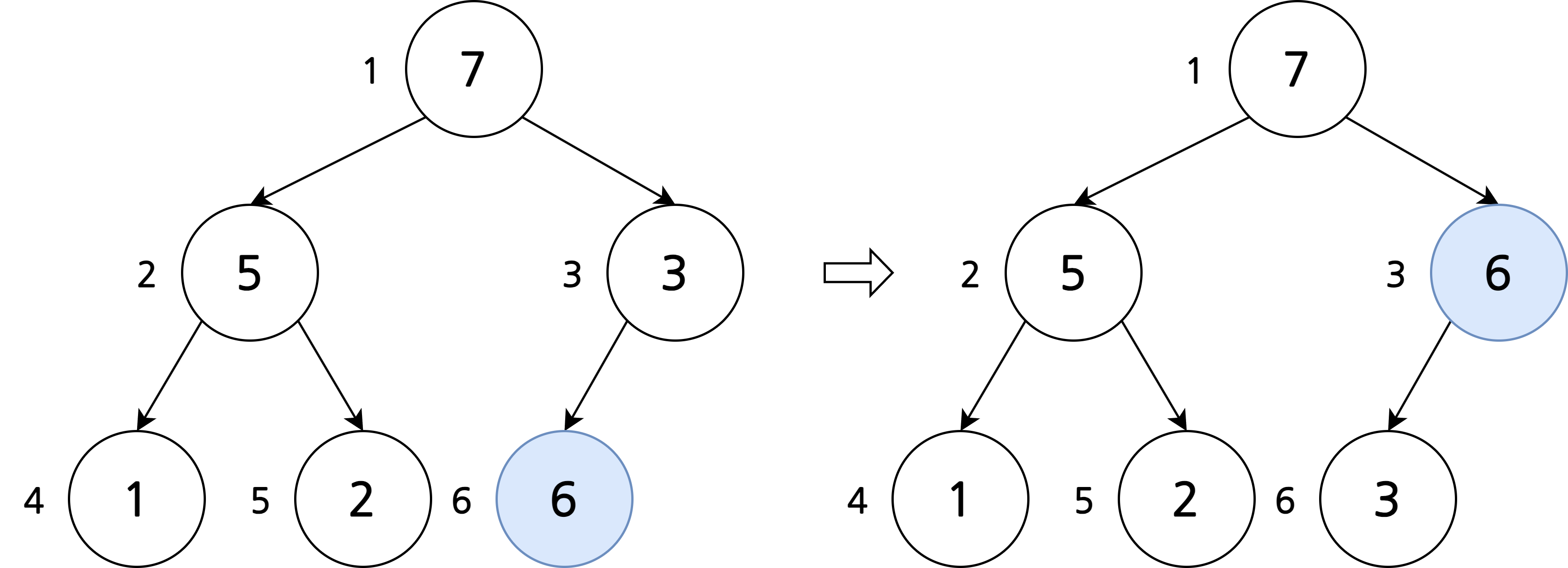
  • 힙의 삽입 연산

    

    1. 마지막 노드에 이어서 새로운 노드 삽입
    2. 부모 노드들과 교환하며 적절한 위치로 이동

    • c언어

      void Insert(Heap* heap, int key)
      {
      	if (IsFull(heap))
      	{
      		return;
      	}
            
      	int i = ++(heap->heapSize);
            
      	while ((i != 1) && (key > heap->heap[i / 2]))
      	{
      		heap->heap[i] = heap->heap[i / 2];
      		i /= 2;
      	}
            
      	heap->heap[i] = key;
      }
      

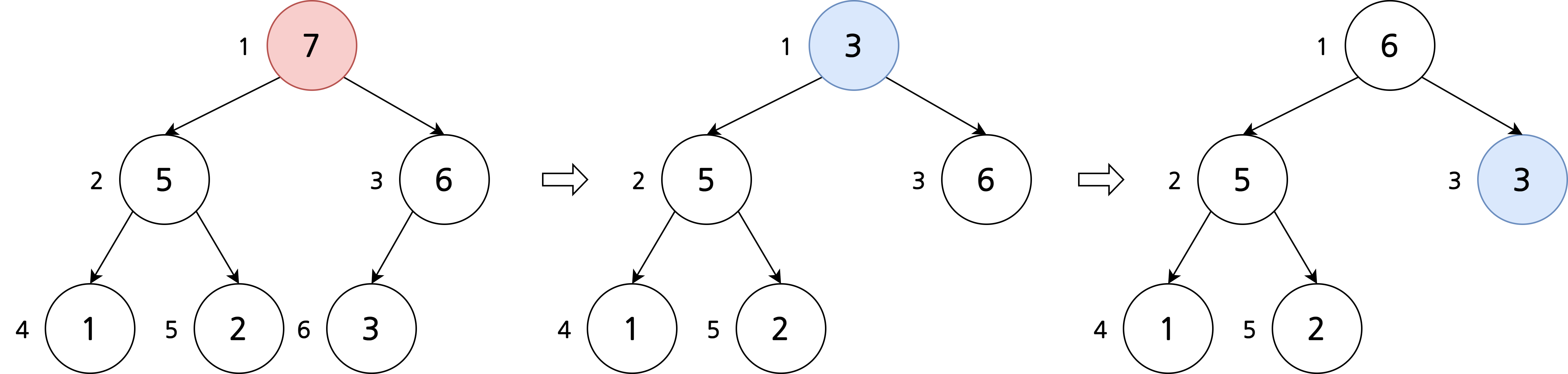
  • 힙의 삭제 연산

    

    1. 루트 노드 삭제
    2. 마지막 노드를 루트 노드로 이동
    3. 자식 노드 중 더 큰 노드와 교환하며 적절한 위치로 이동

    • c언어

      int Delete(Heap* heap)
      {
      	if (IsEmpty(heap))
      	{
      		return -1;
      	}
            
      	int ret = heap->heap[1];
      	int last = heap->heap[(heap->heapSize)--];
      	int i = 1;
      	int next = i * 2;
            
      	while (next <= heap->heapSize)
      	{
      		if ((next < heap->heapSize) && (heap->heap[next] < heap->heap[next + 1]))
      		{
      			++next;
      		}
            
      		if (last >= heap->heap[next])
      		{
      			break;
      		}
            
      		heap->heap[i] = heap->heap[next];
      		i = next;
      		next = i * 2;
      	}
            
      	heap->heap[i] = last;
            
      	return ret;
      }
      

  • 시간복잡도

    • 삽입 연산: \(O(\log n)\)​
    • 삭제 연산: \(O(\log n)\)

힙 정렬(heap sort)

1. 정렬할 \(n\)개의 요소를 힙에 삽입
2. 하나씩 삭제하며 저장

• 힙을 이용한 정렬

• 시간복잡도: \(O(n\log n)\)

  • 요소의 개수가 \(n\)개이고 하나를 삽입하거나 삭제할 때 \(O(\log n)\)이 걸리므로 \(O(n \log n)\)

• 힙 정렬이 유용한 경우

  • 전체 자료가 아닌 큰 값 몇 개만 필요한 경우

• c언어

  // 내림 차순 정렬
  void HeapSort(int array[], int n)
  {
  	Heap* heap = Create();
    
  	for (int i = 0; i < n; ++i)
  	{
  		Insert(heap, array[i]);
  	}
    
  	for (int i = 0; i < n; ++i)
  	{
  		array[i] = Delete(heap);
  	}
    
  	free(heap);
  }