자료구조 9. 그래프

코드

• 모든 코드는 깃허브에서 확인하실 수 있습니다.

그래프

• 연결되어 있는 노드 간의 관계를 표현하는 자료구조
  • 트리도 그래프

그래프 \(G\)

• 그래프 \(G\)는 \((V, E)\)로 표시

• 정점(vertices)
  • 여러가지 특성을 가지는 객체
  • \(V(G)\): 그래프 \(G\)의 정점 집합
  • 노드라고도 불림
  • 예) \(V(G) = \{0, 1, 2, 3\}\)
• 간선(edge)
  • 정점들 간의 관계 의미
  • \(E(G)\): 그래프 \(G\)의 간선 집합
  • 링크라고도 불림
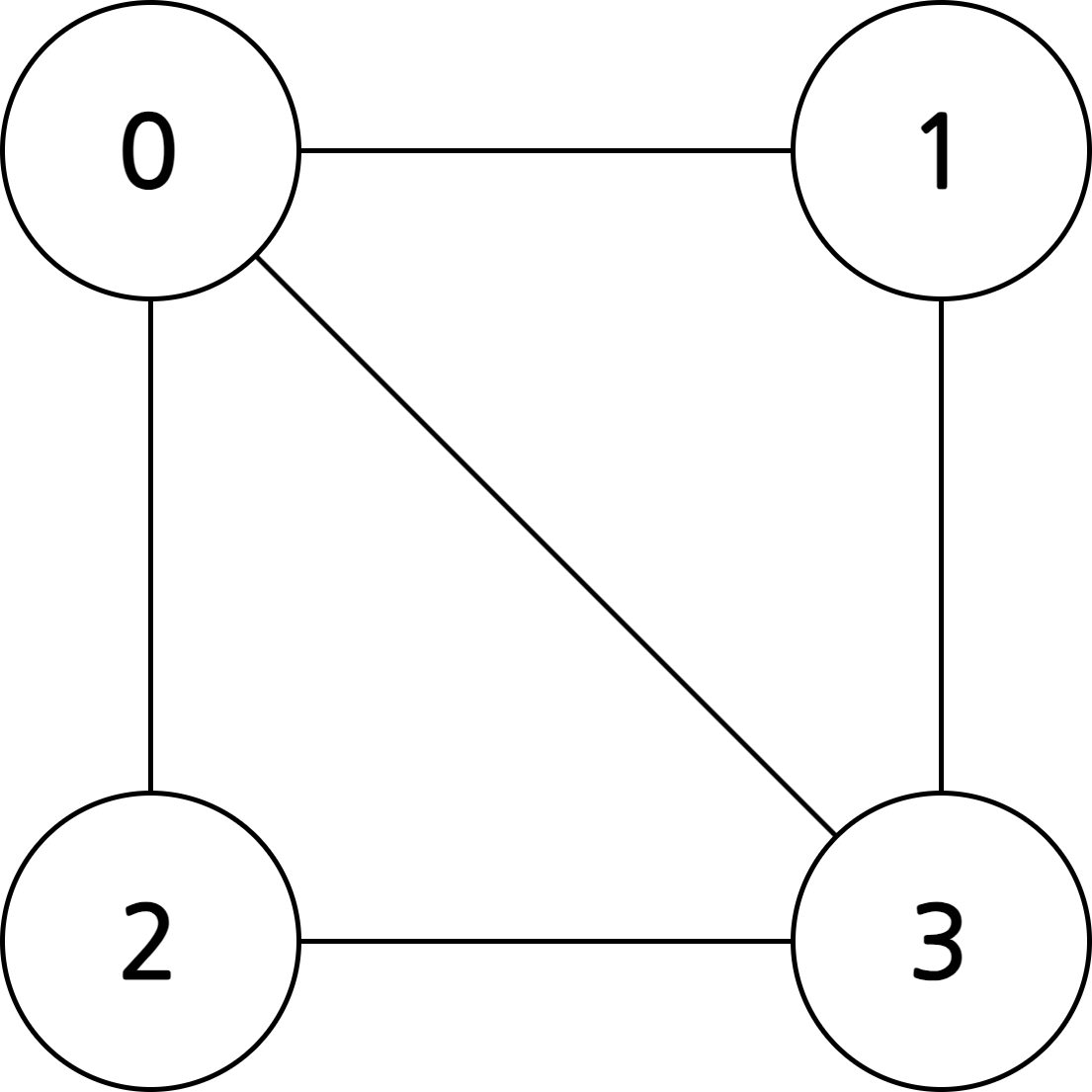
  • 예) \(E(G) = \{(0, 1), (0, 2), (0, 3), (1, 3), (2, 3)\}\)

  • 무방향 그래프

    

    • 간선에 방향이 없는 그래프
    • \(E(G) = \{(0, 1), (0, 2), (0, 3), (1, 3), (2, 3)\}\)처럼 \(()\)를 이용해 간선을 표기

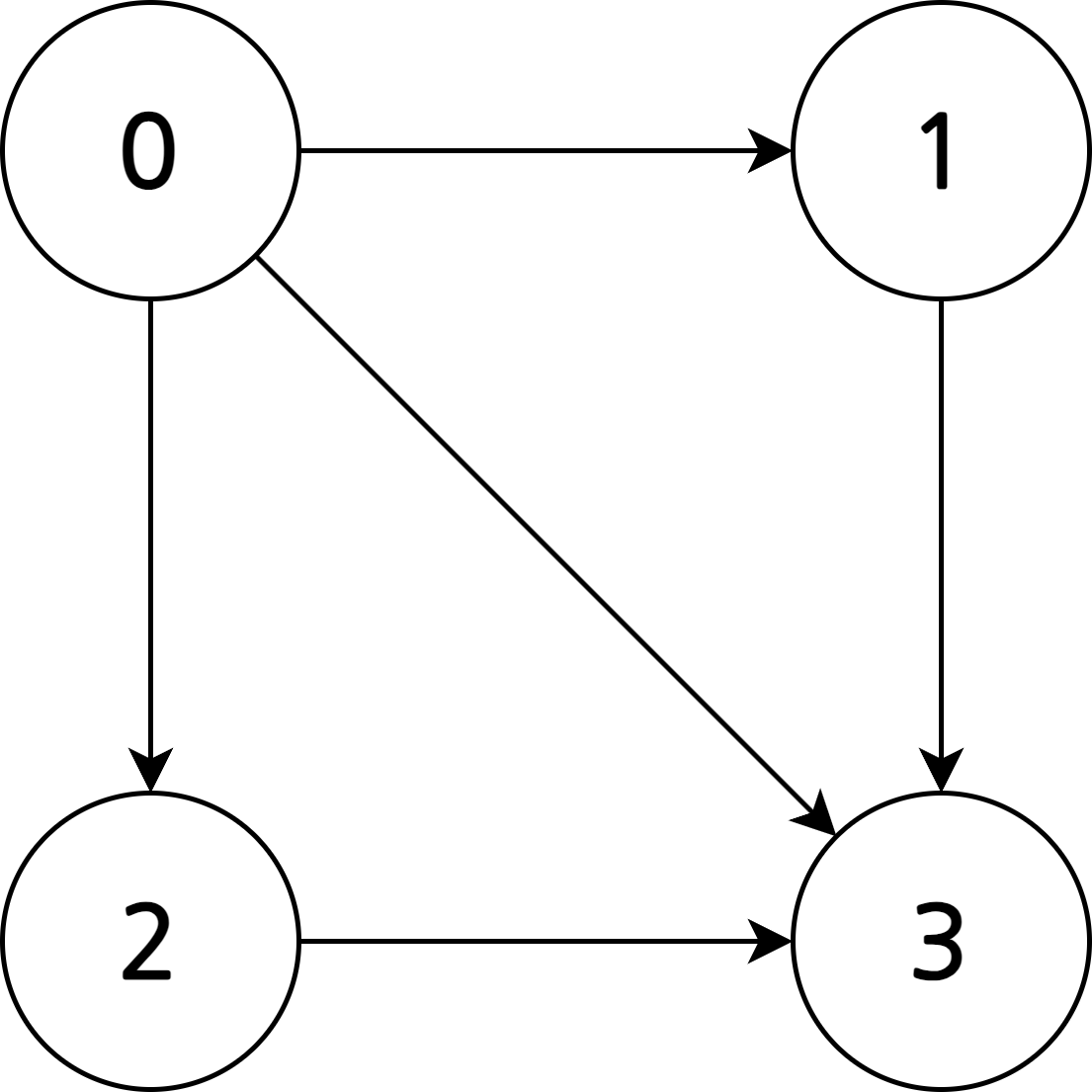
  • 방향 그래프

    그래프 \(G^\prime\)

    • 간선에 방향이 있는 그래프
    • \(E(G) = \{<0, 1>, <0, 2>, <0, 3>, <1, 3>, <2, 3>\}\)처럼 \(<\text{start}, \text{end}>\)​로 간선의 방향을 표기
• 부분 그래프(subgraph)
  • 그래프의 일부로 이루어진 그래프
    • 정점 집합과 간선 집합의 부분 집합으로 이루어진 그래프
  • \(V(S) \subseteq V(G)\), \(E(S) \subseteq E(G)\)​
• 인접 정점(adjacent vertex)
  • 하나의 정점에서 간선에 의해 연결된 정점
  • 예) 그래프 \(G\)에서 정점 \(0\)의 인접 정점: 정점 \(1\), 정점 \(2\), 정점 \(3\)​
• 그래프의 차수(degree)
  • 무방향 그래프
    • 하나의 정점에서 연결된 다른 정점의 수(인접 정점의 수)
    • 예) 그래프 \(G\)에서 정점 \(0\)​의 차수: 3
  • 방향 그래프
    • 진입 차수, 내차수(in-degree): 외부에서 오는 간선의 수
    • 진출 차수, 외차수(out-degree): 외부로 향하는 간선의 후
    • 모든 진입(진출) 차수의 합은 간선의 수
    • 예)
      • 그래프 \(G^\prime\)에서 정점 \(3\)의 내차수: 3
      • 그래프 \(G^\prime\)에서 정점 \(0\)​의 외차수: 3
• 그래프의 경로(path)
  • 정점 \(s\)로부터 정점 \(e\)까지 경로: 정점의 나열 \(s, v1, v2, ..., vk, e\)
    • 단, 반드시 나열된 정점 사이에 간선이 존재해야 함
    • 예) 그래프 \(G\)에서 \(0, 1, 3\)은 경로이지만 \(0, 1, 2\)는 경로가 아님
  • 단순 경로(simple path): 경로 중에 반복되는 간선이 없는 경로
    • 예) 그래프 \(G\)에서 \(0, 1, 3, 2\)
  • 사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경로
    • 예) 그래프 \(G\)에서 \(0, 1, 3, 0\)​
  • 연결 그래프(connected graph): 모든 정점 사이에 항상 경로 존재하는 그래프
  • 완전 그래프(complete graph): 모든 정점이 연결되어 있는 그래프
    • \(n\)개의 정점을 가진 완전 그래프의 간선의 수는 \(\frac{n\times (n - 1)}{2}\)

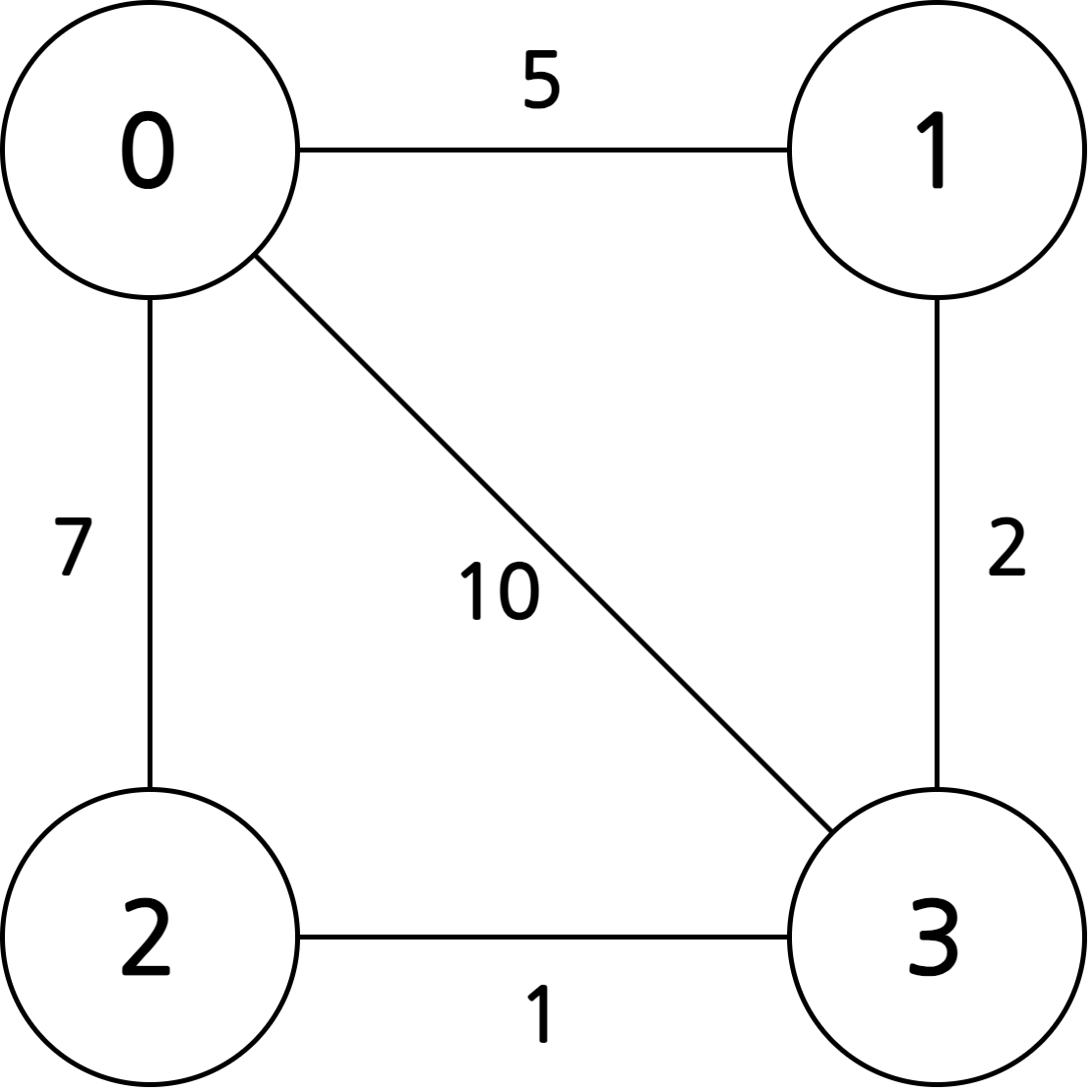
• 네트워크, 가중치 그래프(weighted graph)

  

  • 간선에 비용(cost)이나 가중치(weight)가 할당된 그래프
  • 예) 도시 사이의 거리
• 그래프의 기능
  • create: 그래프 생성
  • is_empty: 그래프가 비었는지 확인
  • is_full: 그래프가 포화 상태인지 확인
  • insert_vertex: 그래프에 정점을 추가
  • delete_vertex: 그래프에 정점을 삭제
  • insert_edge: 그래프에 간선을 추가
  • delete_edge: 그래프에 간선을 삭제
  • adjacent: 정점의 인접 정점을 반환
• 그래프 표현법
  • 인접 행렬 방법
  • 인접 리스트 방법

그래프 표현법

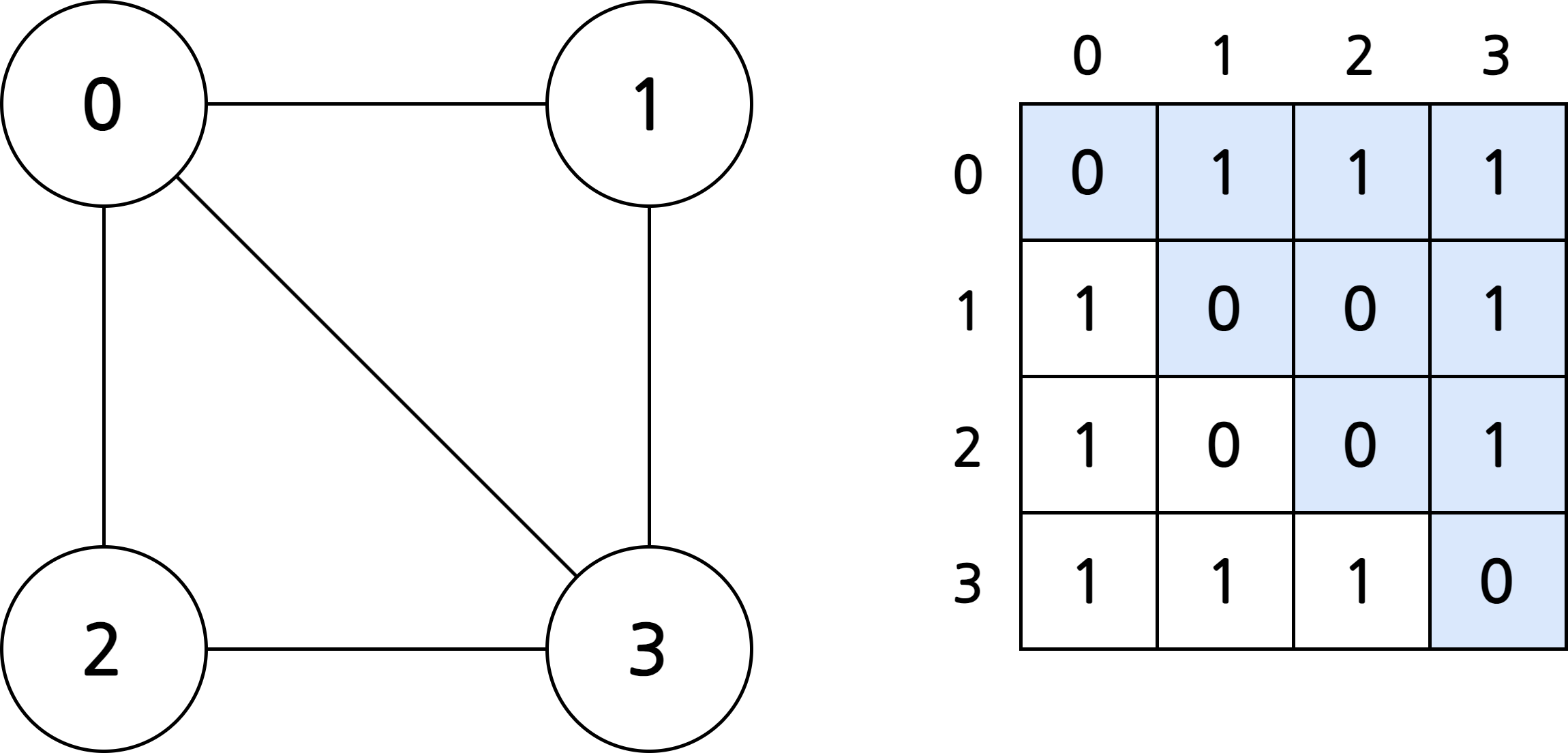
인접 행렬(adjacent matrix) 방법

• 간선을 행렬로 표현하는 방법
• 간선 \((i, j)\)가 존재하면 \(\mathbf{M}_{ij} = 1\)
• 간선 \((i, j)\)가 존재하지 않으면 \(\mathbf{M}_{ij} = 0\)​

• c언어

  • 그래프 구조체

    typedef struct
    {
    	int n;
    	int adjMat[MAX_VERTICES][MAX_VERTICES];
    } Graph;
    

  • IsEmpty

    int IsEmpty(Graph* graph)
    {
    	return graph->size == 0;
    }
    

  • IsFull

    int IsFull(Graph* graph)
    {
    	return graph->size == MAX_VERTICES;
    }
    

  • Create

    Graph* Create()
    {
    	Graph* graph = (Graph*)malloc(sizeof(Graph));
    	if (graph == NULL)
    	{
    		exit(1);
    	}
        
    	graph->n = 0;
        	
    	for (int r = 0; r < MAX_VERTICES; ++r)
    	{
    		for (int c = 0; c < MAX_VERTICES; ++c)
    		{
    			graph->adjMat[r][c] = 0;
    		}
    	}
    }
    

  • InsertVertex

    void InsertVertex(Graph* graph)
    {
    	if (IsFull(graph))
    	{
    		return;
    	}
        
    	++(graph->size);
    }
        
    

  • DeleteVertex

    void DeleteVertex(Graph* graph, int vertex)
    {
    	if ((vertex < 0) || (vertex >= graph->size))
    	{
    		return;
    	}
        
    	for (int r = vertex + 1; r < graph->size; ++r)
    	{
    		for (int c = 0; c < vertex; ++c)
    		{
    			graph->adjMat[r - 1][c] = graph->adjMat[r][c];
    		}
    	}
        
    	for (int c = vertex + 1; c < graph->size; ++c)
    	{
    		for (int r = 0; r < vertex; ++r)
    		{
    			graph->adjMat[r][c - 1] = graph->adjMat[r][c];
    		}
    	}
        
    	for (int r = vertex + 1; r < graph->size; ++r)
    	{
    		for (int c = vertex + 1; c < graph->size; ++c)
    		{
    			graph->adjMat[r - 1][c - 1] = graph->adjMat[r][c];
    		}
    	}
        
    	--(graph->size);
    }
    

  • InsertEdge

    void InsertEdge(Graph* graph, int start, int end)
    {
    	if ((start < 0) || (start >= graph->size) || (end < 0) || (end >= graph->size))
    	{
    		return;
    	}
        
    	graph->adjMat[start][end] = 1;
    	graph->adjMat[end][start] = 1;
    }
    

  • DeleteEdge

    void DeleteEdge(Graph* graph, int start, int end)
    {
    	if ((start < 0) || (start >= graph->size) || (end < 0) || (end >= graph->size))
    	{
    		return;
    	}
        
    	graph->adjMat[start][end] = 0;
    	graph->adjMat[end][start] = 0;
    }
    

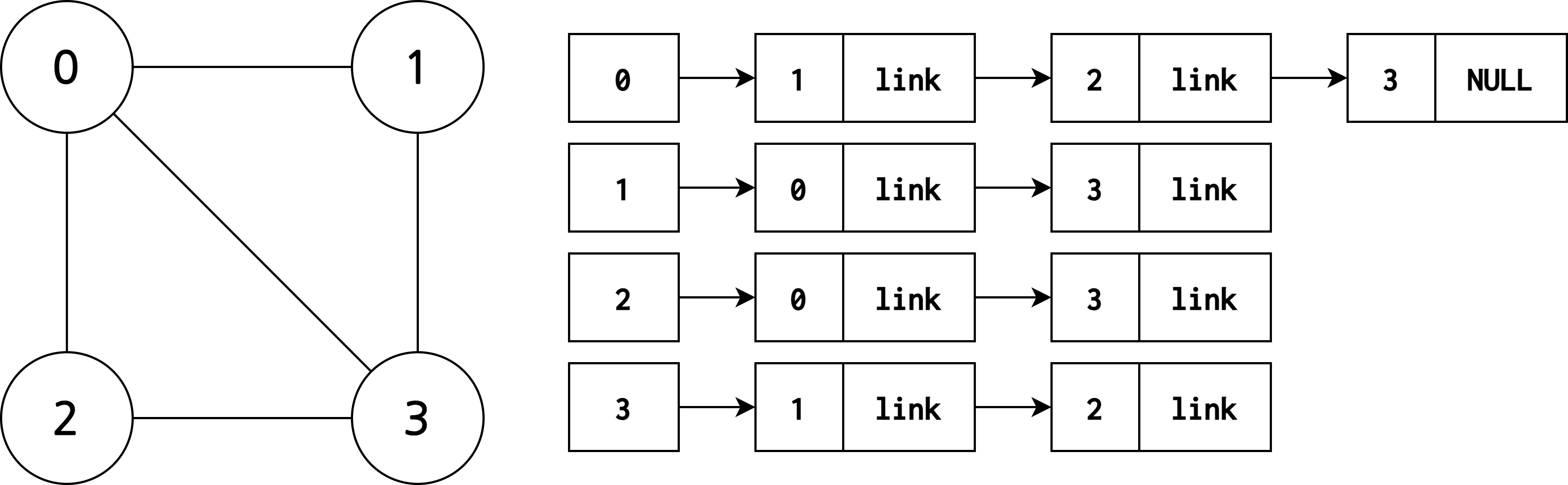
인접 리스트(adjacency list) 방법

• 각 정점에 인접한 정점들을 연결 리스트로 표현

그래프 탐색(graph traversal)

• 그래프의 한 정점에서 모든 정점을 방문하는 과정

깊이 우선 탐색(DFS, Depth First Search)

• 한 방향으로 갈 수 있을 때까지 가다가 가장 가까운 갈림길로 돌아와서 다른 방향을 탐색하는 방법
• 스택을 이용하여 구현

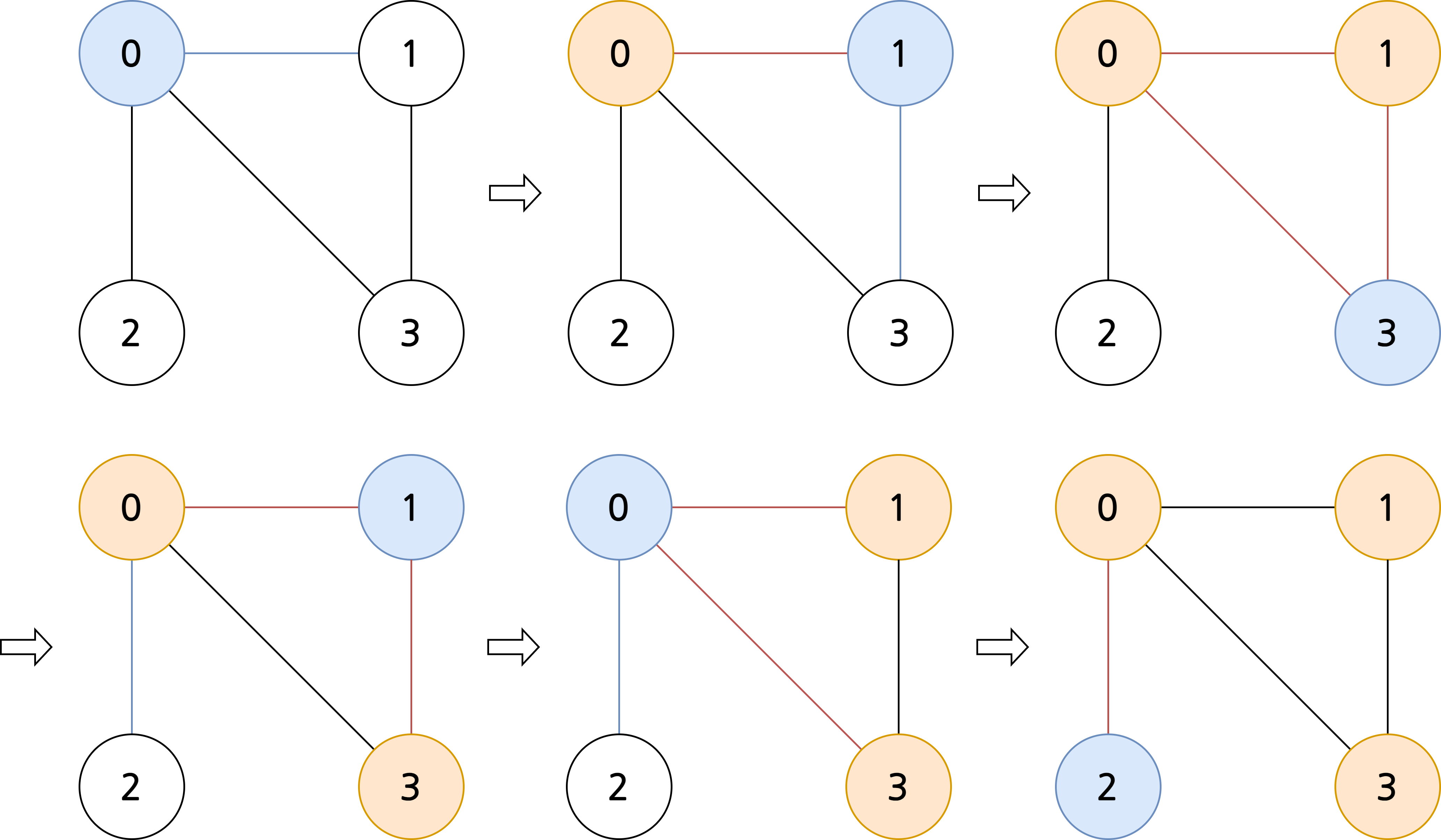
1. 정점 \(0\)에서 탐색 시작
2. 정점 \(1\)​에서 탐색 시작
3. 정점 \(3\)에서 탐색 시작
4. 갈 수 있는 곳이 없어 정점 \(1\)에서 다시 탐색 시작
5. 갈 수 있는 곳이 없어 정점 \(0\)에서 다시 탐색 시작
6. 정점 \(2\)에서 탐색 시작
7. 갈 수 있는 곳이 없어 정점 \(0\)에서 다시 탐색 시작
8. 갈 수 있는 곳이 없어 탐색 종료

• 시간복잡도: \(O(n^2)\)
  • 인접 리스트의 경우 \(O(n + e)\)(\(e\)는 간선의 수)

• c언어

  void DFS(Graph* graph, int startVertex)
  {
  	static int visited[MAX_VERTICES] = { 0, };
    
  	visited[startVertex] = 1;
  	printf("%d -> ", startVertex);
    
  	for (int i = 0; i < graph->size; ++i)
  	{
  		if (graph->adjMat[startVertex][i] && !visited[i])
  		{
  			DFS(graph, i);
  		}
  	}
  }
  

넓이 우선 탐색(BFS, Breadth First Search)

• 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 탐색하는 방법
• 큐를 이용하여 구현

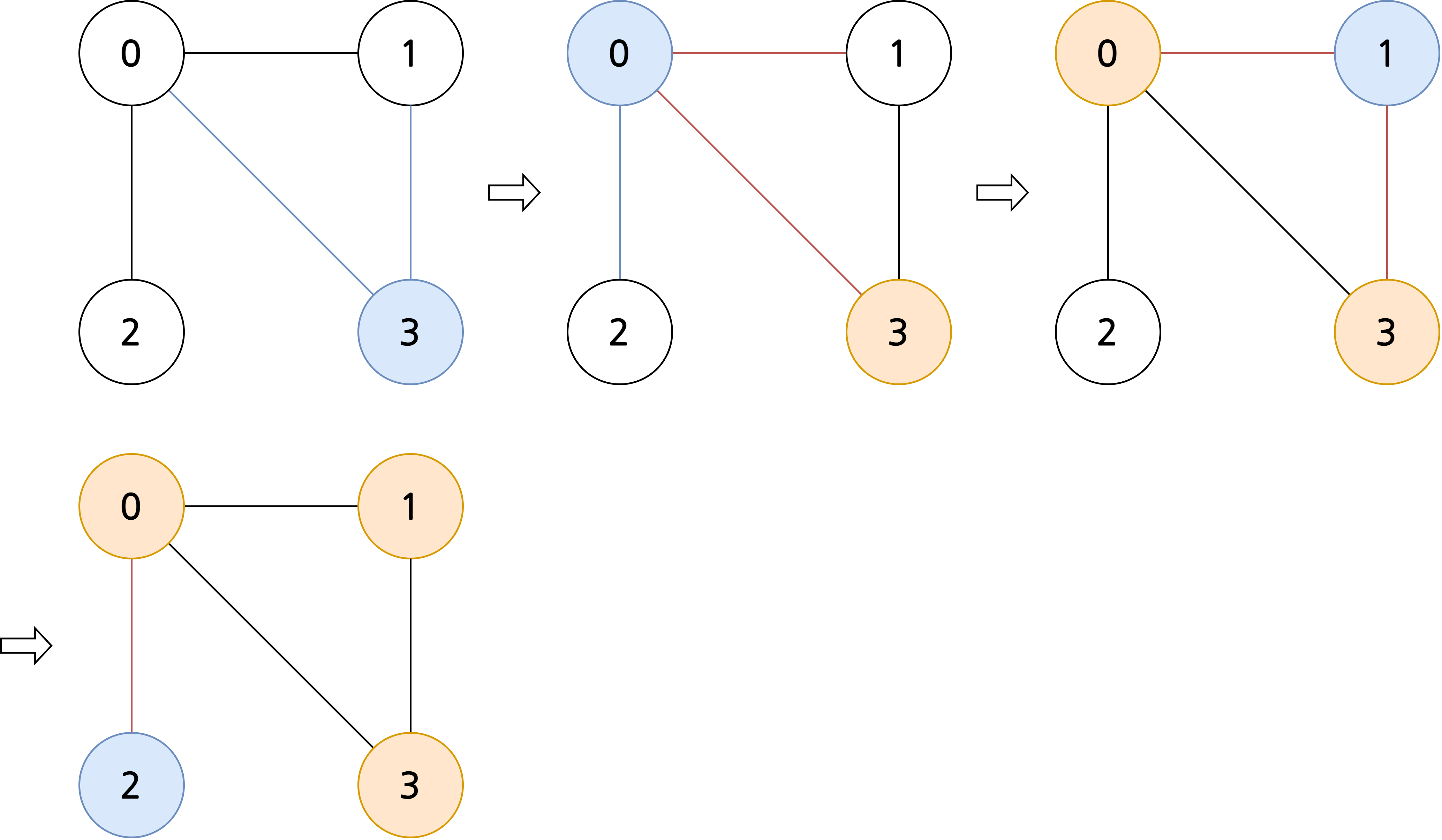
1. 정점 \(3\)에서 탐색 시작, 정점 \(0\)과 \(1\) 탐색 가능
2. 정점 \(0\)에서 탐색 시작, 정점 \(2\) 탐색 가능
3. 정점 \(1\)에서 탐색 시작, 탐색 가능한 정점 없음
4. 정점 \(2\)에서 탐색 시작, 탐색 가능한 정점 없음, 탐색 종료

• 시간복잡도: \(O(n^2)\)

  • 인접 리스트의 경우 \(O(n + e)\)(\(e\)는 간선의 수)

• c언어

  void BFS(Graph* graph, int startVertex)
  {
  	static int visited[MAX_QUEUE_SIZE] = { 0, };
  	Queue queue = { .front = 0, .rear = 0 };
    
  	visited[startVertex] = 1;
  	Enqueue(&queue, startVertex);
    
  	while (!IsEmptyQueue(&queue))
  	{
  		int vertex = Dequeue(&queue);
  		printf("%d -> ", vertex);
    
  		for (int i = 0; i < graph->size; ++i)
  		{
  			if (graph->adjMat[vertex][i] && !visited[i])
  			{
  				visited[i] = 1;
  				Enqueue(&queue, i);
  			}
  		}
  	}
  }