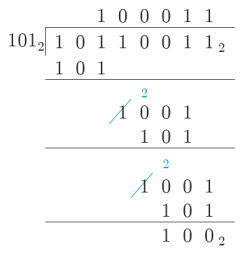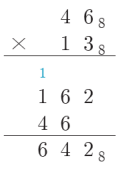이산수학 1. 수의 표현과 연산

1. 수의 체계

수 표현

• 기수(base): 수 표현의 근거, \(n\)진수에서의 \(n\)
  • 아래 첨자로 표기
  • 예)
    • \(123_{10}\): 10진수
    • \(1011_2\): 2진수

• 자릿수: 수를 구성하는 각 숫자의 위치

  • 예) \(123.4567_{10}\)

    \(123.4567_{10}\)	\(1\)	\(2\)	\(3\)	.	\(4\)	\(5\)	\(6\)	\(7\)
    자릿수	\(2\)	\(1\)	\(0\)		\(-1\)	\(-2\)	\(-3\)	\(-4\)

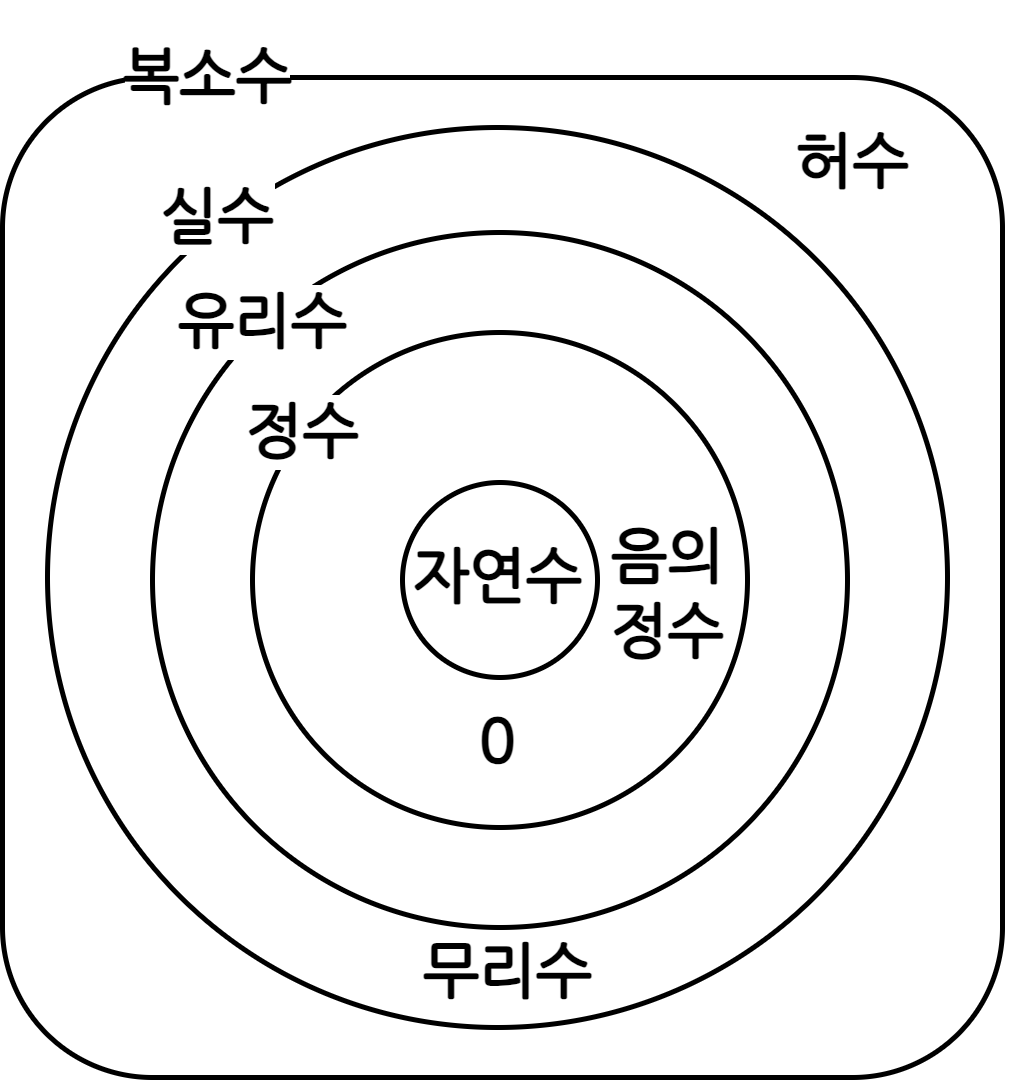
수의 체계

• 자연수(natural number): \(\mathbb{N}\) \(n= a_k b^k + a_{k-1} b^{k-1} + \cdots + a_1 b^1 + a_0 b_0\)

  • \(b\): 기수, \(b\in\mathbb{N}\), \(b\gt1\)
  • \(a_i\): 자연수 \(n\)을 구성하는 \(i\)번째 숫자(\(i \ge 0\)), \(a_i\in\mathbb{N}\cup\{0\}\), \(0\le a_i\lt b\)
  • \(k\): 자릿수
  • 예)
    • 10진수: \(589_{10}=5\times 10^2 + 8\times 10^1 + 9\times 10^0\)
    • 2진수: \(1110_2 = 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0\)

• 정수(integer): \(\mathbb{Z}\)

  • 양의 정수, \(0\), 음의 정수로 구성된 수
  • \(0\): 양의 정수나 음의 정수에 속하지 않은 수
  • 음의 정수: \(-\), \(0\)보다 작은 수
  • 양의 정수: \(+\), \(0\)보다 큰 수

• 유리수(rational number): \(\mathbb{Q}\) \(\frac{b}{a}\)

  • \(a, b \in \mathbf{Z}\), \(a \neq 0\)
  • 하한항(lowest)
    • \(1\) 이외의 공약수가 존재하지 않는 분모와 분자
    • \(2=\frac{2}{1}\)과 같은 정수도 해당
    • 예) \(\frac{6}{27}\)의 하한항은 \(\frac{2}{9}\)

• 무리수(irrational number): \(\mathbb{I}\)

  • 분수로 표현될 수 없는 실수
  • 예) \(\sqrt{2}\)

• 실수(real number): \(\mathbb{R}\) \(r= a_k b^k + a_{k-1} b^{k-1} + \cdots + a_1 b^1 + a_0 b_0 + a_{-1}b^{-1} + a_{-2}b^{-2} + \cdots\)

  • \(b\): 기수, \(b\in\mathbb{N}\), \(b\gt1\)
  • \(a_i\): 실수 \(r\)을 구성하는 \(i\)번째 숫자(\(i \in \mathbb{Z}\)), \(a_i\in\mathbb{Z}\), \(0\le a_i\lt b\)
  • \(k\): 자릿수
  • 예)
    • 10진수: \(123.45_{10}=1\times10^2+2\times10^1+3\times10^0+4\times10^{-1}+5\times10^{-2}\)
    • 2진수: \(10.101_2=1\times2^1+0\times2^0+1\times2^{-1}+0\times2^{-2}+1\times2^{-3}\)

• 복소수(complex number): \(\mathbb{C}\)

  • 실수와 허수를 모두 포함하는 수 체계
  • 허수 단위(imaginary unit)
    • \(i^2=-1\)를 만족하는 수 \(i\)
  • 복소수의 사칙연산(\(a, b, c, d \in \mathbb{R}\))
    • 덧셈: \((a + bi) + (c + di) = (a + c) + (b + d)i\)
    • 뺄셈: \((a + bi) - (c + di) = (a - c) + (b - d)i\)
    • 곱셈: \((a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i\)
    • 나눗셈: \(\frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{ac - adi + bci + bd}{c^2 - cdi + cdi + d^2} = \left( \frac{ac + bd}{c^2 + d^2} \right) + \left( \frac{bc - ad}{c^2 + d^2} \right)i\) (단, \(c+di\neq0\))

2. 수의 연산

연산의 성질

• 닫힘 성질: 수 체계 \(S\)에 속하는 어떤 수 \(a\), \(b\)를 연산자 \(O\)로 연산한 결과가 \(S\)에 속하면 ‘\(S\)는 \(O\)에 대해 닫혀있다(closed)’라고 함

  • 수 체계별 사칙연산의 닫힘 여부

    	덧셈	뺄셈	곱셈	나눗셈
    자연수 \(\mathbb{N}\)	O	X	O	X
    정수 \(\mathbb{Z}\)	O	O	O	X
    유리수 \(\mathbb{Q}\)	O	O	O	O
    무리수 \(\mathbb{I}\)	X	X	X	X
    실수 \(\mathbb{R}\)	O	O	O	O
    복소수 \(\mathbb{C}\)	O	O	O	O

    • 자연수 - 자연수: 0, 음수의 정수가 될 수도 있음
    • 자연수 / 자연수, 정수 / 정수: 유리수가 될 수도 있음
    • 무리수 + 무리수: \(\sqrt{2}+(-\sqrt{2})=0\), 0은 정수로 무리수가 아님
    • 무리수 - 무리수: \(\sqrt{2}-\sqrt{2}=0\)
    • 무리수 * 무리수: \(\sqrt{2} \times \sqrt{2} = 2\)
    • 무리수 / 무리수: \(\sqrt{2} \div \sqrt{2}=1\)

  • 무리수가 아닌 경우 교환, 결합, 분배 법칙이 성립(덧셈, 곱셈에서 닫혀있기 때문)

• 항등원(identity element)

  • \(a, b \notin \mathbb{I}\)이고 연산자 \(O\)에 대해 닫여 있을 때, 모든 수 \(a\)에 대하여 \(a\;O\;b = b\;O\;a = a\)를 만족하는 \(b\)
  • 합에 대한 항등원: 0
    • \(a + 0 = 0 + a = a\)를 만족
  • 곱에 대한 항등원: 1
    • \(a \times 1 = 1 \times a = a\)를 만족

• 역원(inverse element)

  • \(a, b, c \notin \mathbb{I}\)이고 \(a, b\)가 연산자 \(O\)에 대해 닫혀 있으며 \(c\)가 연산자 \(O\)에 대한 항등원일 때, \(a\;O\;b = b\;O\;a = c\)를 만족하는 \(b\)
  • \(a\)의 합에 대한 역원: \(-a\)
  • \(a\)의 곱에 대한 역원: \(\frac{1}{a}\)(단, \(a\neq0\))

합 연산

\[\sum_{i=1}^na_i=a_1+a_2+\cdots+a_{n-1}+a_n\]

• 합 연산의 성질

  \[\begin{align*} &\sum_{i=1}^{n} c = nc \\ &\sum_{i=1}^{n} cx_i = c \sum_{i=1}^{n} x_i \\ &\sum_{i=1}^{n} (x_i + y_i) = \sum_{i=1}^{n} x_i + \sum_{i=1}^{n} y_i \\ &\sum_{i=1}^{n} x_i = \sum_{i=1}^{k} x_i + \sum_{i=k+1}^{n} x_i \quad (\text{where } 1 \leq k < n) \end{align*}\]

곱 연산

\[\prod_{i=1}^na_i=a_1\times a_2\times\cdots\times a_{n-1}\times a_n\]

• 곱 연산의 성질

  \[\begin{align*} &\prod_{i=1}^{n} c = c^n \\ &\prod_{i=1}^{n} x_i y_i = \prod_{i=1}^{n} x_i \times \prod_{i=1}^{n} y_i \\ &\prod_{i=1}^{n} x_i = \prod_{i=1}^{k} x_i \times \prod_{i=k+1}^{n} x_i \quad (\text{where } 1 \leq k < n) \end{align*}\]

• 펙토리얼(factorial)

  \[n!=1\times2\times3\times\cdots\times n=\prod_{i=1}^n i\]
  • \(n\in\mathbb{N}\)일 때, 1부터 \(n\)까지 1씩 증가하는 수열의 곱

나누기 연산

\[n=dq+r\]

• 정수 \(n\)을 자연수 \(d\)로 나누었을 때의 몫을 \(q\), 나머지를 \(r\)이라고 했을 때의 식
  • \(r=0\)일 때, \(n\)은 \(d\)로 나누어떨어진다고 하고, \(d\mid n\)과 같이 표기
  • \(r\neq0\)일 때, \(n\)은 \(d\)로 나누어떨어지지 않는다고 하고, \(d\nmid n\)과 같이 표기
  • 나누어떨어진다의 성질(\(a, b, c, d, m, n \in \mathbb{Z}\))
    • \(d\mid m\)이고 \(d\mid n\)이면, \(d\mid(m+n)\), \(d\mid(m-n)\)
    • \(d\mid m\)이면, \(d\mid mn\)
    • \(a\mid b\)이고 \(b\mid c\)이면, \(a\mid c\)
• 몫을 구하는 연산: \(\text{div}\)
  • 사용법: \(q = n\;\text{div}\;d\)
• 나머지를 구하는 연산: \(\text{mod}\)
  • 사용법: \(r=n\;\text{mod}\;d\)

3. 진법별 표현

• 10진법

  \[n_{10} = a_k10^k + a_{k-1}10^{k-1}+\cdots+a_1 10^1+a_0 10^0 \; ((a_ka_{k-1}...a_1a_0)_{10})\]
  • 10을 기수로 사용
  • 0~9를 이용해 표현

• 2진법

  \[n_{10} = b_k2^k + b_{k-1}2^{k-1}+\cdots+b_1 2^1+b_0 2^0 \; ((b_kb_{k-1}...b_1b_0)_2)\]
  • 2를 기수로 사용
  • 0과 1을 이용해 표현

• 8진법

  \[n_{10} = o_k8^k + o_{k-1}8^{k-1}+\cdots+o_1 8^1+o_0 8^0 \; ((o_ko_{k-1}...o_1o_0)_8)\]
  • 8을 기수로 사용
  • 0~7을 이용해 표현

• 16진법

  \[n_{10} = x_k16^k + x_{k-1}16^{k-1}+\cdots+x_1 16^1+x_0 16^0 \; ((x_kx_{k-1}...x_1x_0)_16)\]
  • 16을 기수로 사용
  • 0~9와 A(10), B(11), C(12), D(13), E(14), F(15)를 이용해 표기

4. 진법 간 변환

10진수 → 2진수 / 8진수 / 16진수

• 10진수 정수부
  • 몫이 0이 될 때까지 변환하려는 기수로 나누면서 각 단계마다 나머지를 나열
  • 가장 먼저 얻은 나머지부터 낮은 자릿수에 배치
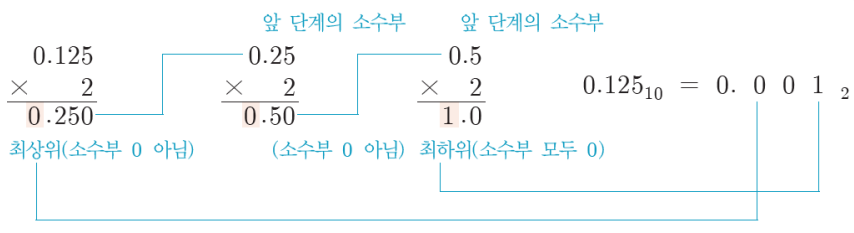
• 10진수 소수부(소수점 밑)
  • 소수부0이 될 때까지 변환하려는 기수로 곱하면서 각 단계마다 정수부를 나열
    • 각 단계마다 정수부는 0으로 초기화
  • 가장 먼저 얻은 정수부부터 소수점 밑에 가깝게 배치
• 예)
  • \(83.125_{10}\)를 2진수로 변환

    • 정수부: \(83\)

      

    • 소수부: \(125\)

      

    • 결과: \(82.125_{10}=1010011.001_2\)

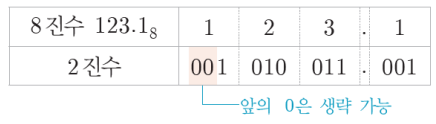
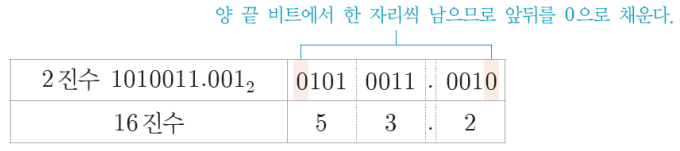
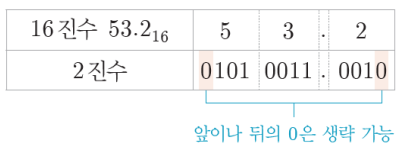
2진수 ↔ 8진수 / 16진수

• 2진수 → 8진수
  • 3자리(\(2^3=8\)​)씩 끊어서 변환
  • 예)

    • \(1010011.001_2\)를 8진수로 변환

      

• 8진수 → 2진수
  • 각 자리 숫자를 2진수로 변환
  • 예)

    • \(123.1_8\)을 2진수로 변환

      

• 2진수 → 16진수
  • 4자리(\(2^4=16\))씩 끊어서 변환
  • 예)

    • \(1010011.001_2\)를 16진수로 변환

      

• 16진수 → 2진수

  • 각 자리 숫자를 2진수로 변환
  • 예)

    • \(53.2_{16}\)를 2진수로 변환

      

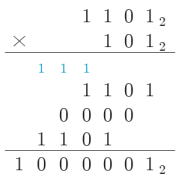
5. 진법 별 사칙연산

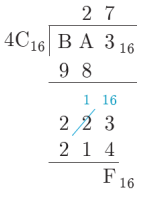
• 10진수를 더하는 방법과 같음
  • 단지 진법이 변했을 뿐
• 예)

  • \(1101_2 \times 101_2\) (2진수 곱셈)

    

  • \(10110011_2 \div 101_2\) (2진수 나눗셈)

    

  • \(46_8 \times 13_8\) (8진수 곱셈)

    

  • \(\text{B}\text{A}3_{16} \div 4\text{C}_{16}\) (16진수 나눗셈)

    

6. 보수

보수(complement)

• 어떤수 \(a\)에 대한 \(n\)의 보수: \(a\)와의 합이 \(n\)이 되는 수
  • 10진수 \(1\)에 대한 \(9\)의 보수: \(1 + x = 9\), \(x=8\)
  • 5진수 \(1\)에 대한 \(5\)의 보수: \(1 + x = 5\), \(x = 4\)
• \(1\)의 보수: 어떤 2진수 \(a\)와의 합이 \(1\)(\(1_2\)​)이 되는 수
  • \(0_2\)에 대한 \(1\)의 보수: \(0_2 + x = 1_2\), \(x = 1_2\)
  • \(1_2\)에 대한 \(1\)의 보수: \(1_2 + x = 1_2\), \(x = 0_2\)
• \(2\)의 보수: 어떤 2진수 \(a\)와의 합이 \(2\)(\(10_2\))가 되는 수
  • \(0_2\)에 대한 \(2\)의 보수: \(0_2 + x = 0_2\), \(x=0_2\)
  • \(1_2\)에 대한 \(2\)의 보수: \(1_2 + x = 10_2\), \(x = 1_2\)​
  • \(1\)의 보수 \(+1\)
• 예)
  • \(1101011_2\)에 대한 \(1\)의 보수: \(0010100_2\)
  • \(1101011_2\)에 대한 \(2\)의 보수: \(0010101_2\)​

컴퓨터에서의 수의 표현

• 워드(word): 데이터 처리 단위
  • LSB: 최하위 비트
  • MSB: 최상위 비트
    • MSB는 주로 부호를 나타냄
    • MSB가 \(0\)이면 \(+\), \(1\)이면 \(-\)​
  • 예)
    • 4바이트인 경우 LSB는 1번째 비트, MSB는 32번째 비트
• 부호-절댓값 표현(sign-magnitude)
  • 데이터의 절댓값으로 표현하는 방식
  • 예)
    • \(+53_{10}=00110101_2\), \(-53_{10}=10110101_2\)
    • MSB(부호)만 다르고 나머지는 같음
  • 정수에는 사용하지 않는 방식(실수에 사용)
    • \(+0\)과 \(-0\)이 다름
    • \(+a-a\)가 \(0\)이 아닌 경우가 있음
• 부호-1의 보수 표현(sign-1’s complement)
  • 데이터의 절댓값에 대한 \(1\)의 보수로 표현하는 방식
  • 예)
    • \(+53_{10}=00110101_2\), \(-53_{10}=11001010_2\)
    • \(1\)의 보수로 음수 표현
  • 정수에서 사용하지 않는 방식(하드웨어 회로에서 사용)
    • \(+0\)과 \(-0\)​이 다름
  • 초과한 값은 다시 LSB에 더함
• 부호-2의 보수 표현(sign-2’s complement)
  • 데이터의 절댓값에 대한 2의 보수로 표현하는 방식
  • 예)
    • \(+53_{10}=00110101_2\), \(-53_{10}=11001011_2\)
    • \(2\)의 보수로 음수 표현
  • 정수에 사용
    • \(+0\)과 \(-0\)이 같음(넘친 비트는 버림)
    • \(+a-a\)는 \(0\)
  • 초과한 값은 버림
  • 부호-2의 보수 표현을 10진수로 변환
    • 방법1: MSB(부호)를 제외한 비트를 2의 보수를 취해 10진수로 변환한 뒤 \(-\)를 추가
    • 방법2: MSB(부호)를 제외한 비트를 10진수로 변환한 뒤 \(-2^{n-1}\)와 덧셈
• 워드 크기(1워드가 \(n\)비트)에 따른 데이터 표현 범위
  • 부호-절댓값 표현 범위: \(-(2^{n-1}-1)\sim(2^{n-1}-1)\)
  • 부호-1의 보수 표현 범위: \(-(2^{n-1}-1)\sim(2^{n-1}-1)\)
  • 부호-2의 보수 표현 범위: \(-2^{n-1}\sim(2^{n-1}-1)\)