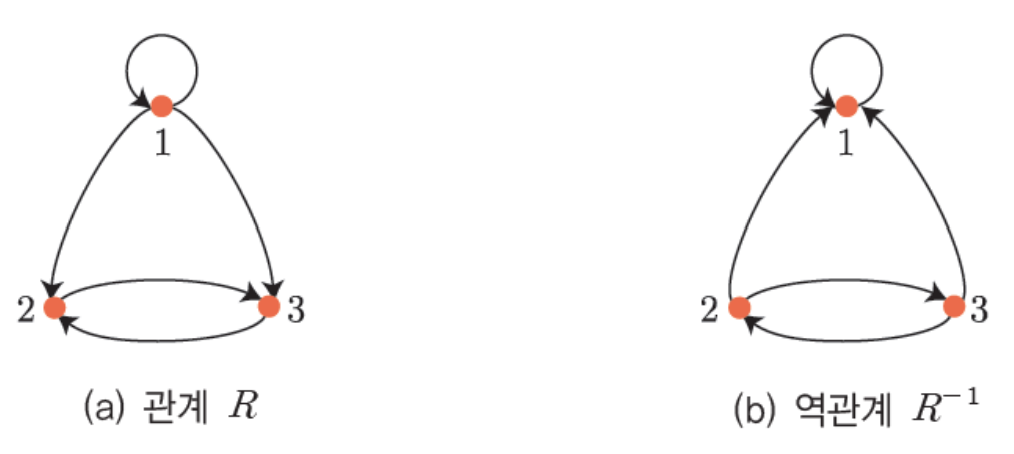Post

이산수학 6. 관계

Posted
Unsplash의 Philip Oroni
Unsplash의 Philip Oroni
By Seyeon Lee 10 min read

1. 관계의 개념

  • 관계(relation, \(R\): \(A \rightarrow B\), \({}_{a}R_{b}\)) / 이항관계(binary relation): 집합 \(A\), \(B\)가 있을 때, \(A\)에서 \(B\)로 가는 관계, \(A \times B\)의 부분집합
    • 예) \(\{(a_1, b_2), (a_2, b_5), (a_3, b_1)\}\)
  • 정의역(domain, \(\text{dom}(R)\)): \(R\)에 속한 순서쌍의 첫 번째 원소가 포함된 집합, \(\text{dom}(R) = \{a \mid a \in A \}\)
  • 공역(codomain, \(\text{codom}(R)\)): \(R\)에 속한 순서쌍의 두 번째 원소가 포함된 집합, \(\text{codom}(R) = \{ b \mid b \in B \}\)
  • 치역(range, \(\text{ran}(R)\)): \(R\)에 속한 순서쌍의 두 번째 원소를 모아놓은 집합, 공역의 부분집합, \(\text{ran}(R) = \{b \mid (a, b) \in R \}\)
  • \(n\)항 관계(\(n\)-ary relation): \(n\)개의 집합 \(A_1, A_2, \cdots, A_n\)이 있을 때, \(A_1 \times A_2 \times \cdots \times A_n\)의 부분집합
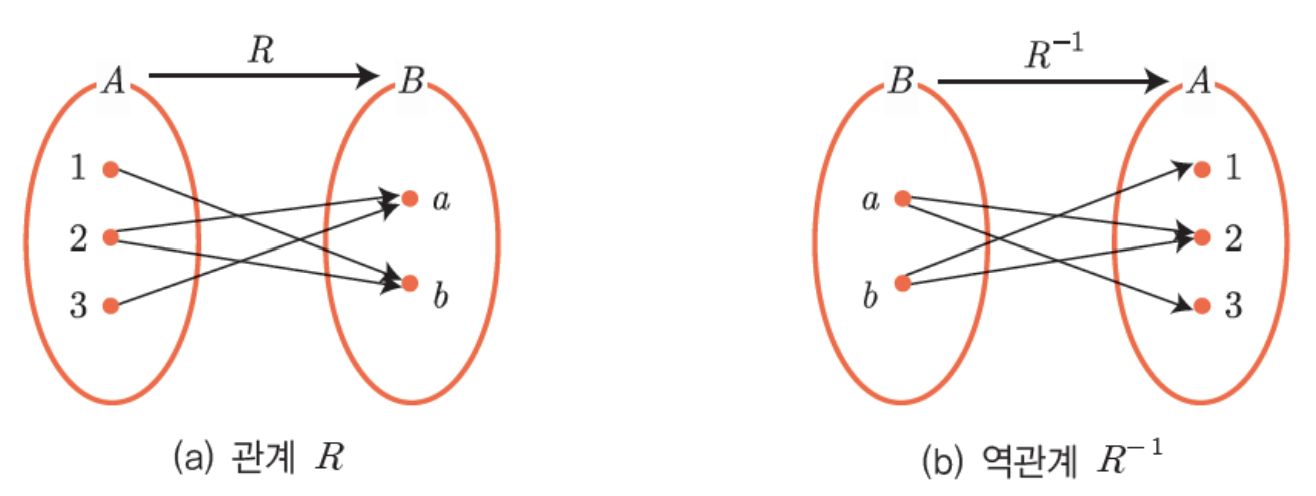
  • 역관계(inverse relation, \(R^{-1}\)): \(A\)에서 \(B\)로의 관계 \(R\)이 있을 때, \(B\)에서 \(A\)로의 관계, \(R^{-1} = \{(b, a) \in B \times A \mid (a, b) \in R \}\)

2. 관계의 표현

arrow_diagram

  • 화살표 선도(arrow diagram): \(R\)을 화살표로 나타낸 도표

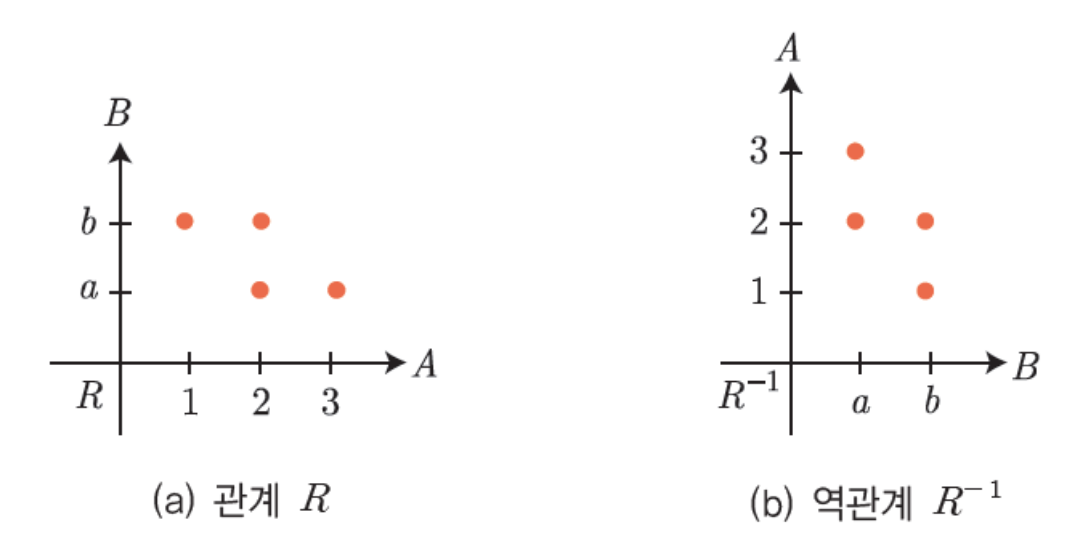
coordinate_diagram

  • 좌표 도표(coordinate diagram): \(R\)에서 \(A\)(정의역)의 원소를 \(x\)축에, \(B\)(공역)의 원소를 \(y\)축에 표시하여 좌표로 나타낸 도표
  • 관계 행렬(relation matrix): \(R\)의 순서쌍을 행렬로 표기
    • \(A\)의 원소가 \(m\)개, \(B\)의 원소가 \(n\)개일 때, \(M_R\)은 \(m \times n\) 행렬
    • 순서쌍에 속한 원소는 1로, 나머지는 0으로 표기

directed_graph

  • 방향 그래프(directed graph): 하나의 집합 \(A\)에서 \(A\)로 가는 관계 \(R\)을 꼭짓점과 화살표를 이용하여 나타낸 그래프

3. 관계의 성질

  • 반사 관계(reflexive relation): \(A\)에 대한 관계 \(R\)이 있을 때, 모든 \(a \in A\)에 대해 \((a, a) \in R\)인 관계
    • 관계 행렬에서 대각선이 모두 1
  • 비반사 관계(irreflexive relation): \(A\)에 대한 관계 \(R\)이 있을 때, 모은 \(a \in A\)에 대해 \((a, a) \notin R\)인 관계
    • 관계 행렬에서 대각선이 모두 0
  • 대칭 관계(symmetric relation): 어떤 \(a, b \in A\)에 대해 \((a, b) \in R\)이면 \((b, a) \in R\)인 관계
  • 반대칭 관계(antisymmetric relation): 어떤 \(a, b \in A\)에 대해 \((a, b) \in R\)이고 \((b, a) \in R\)이면 \(a = b\)인 관계
  • 추이 관계(transitive relation): 어떤 \(a, b, c \in A\)에 대해 \((a, b) \in R\)이고, \((b, c) \in R\)이면 \((a, c) \in R\)인 관계

4. 합성 관계

  • 합성 관계(composite relation, \(S \circ R\)): \(A\)에서 \(B\)로의 관계 \(R\)과 \(B\)에서 \(C\)로의 관계 \(S\)가 있을 때, 이 두 관계를 이용해 구하는 \(A\)에서 \(C\)로의 관계

  • 합성 관계는 관계 행렬의 곱으로 나타낼 수 있음

    • 예)

      • 집합 \(A = \{a, b, c, d\}\), \(B = \{1, 2, 3\}\), \(C = \{x, y, z\}\)에 대한 관계

      • 관계 \(R = \{(a, 2), (b, 2), (b, 3), (c, 1), (d, 1), (d, 2), (d, 3)\}\)

        \[M_R = \begin{bmatrix} 0 & 1 & 0\\ 0 & 1 & 1\\ 1 & 0 & 0\\ 1 & 1 & 1\\ \end{bmatrix}\]

      • 관계 \(S = \{(1, x), (1, z), (2, y), (2, z), (3, x), (3, y)\}\)

        \[M_s = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 1\\ 1 & 1 & 0\\ \end{bmatrix}\]

      • 합성 관계 \(S \circ R = \{(a, y), (a, z), (b, x), (b, y), (b, z), (c, x), (c, z), (d, x), (d, y), (d, z)\}\)

        \[M_{S \circ R} = M_R \odot M_S = \begin{bmatrix} 0 & 1 & 0\\ 0 & 1 & 1\\ 1 & 0 & 0\\ 1 & 1 & 1\\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 1\\ 1 & 1 & 0\\ \end{bmatrix} = \begin{bmatrix} 0 & 1 & 1\\ 1 & 1 & 1\\ 1 & 0 & 1\\ 1 & 1 & 1\\ \end{bmatrix}\]

  • 합성 관계의 거듭제곱(\(R^n\)): 관계 \(R\)에 대하여 \(n\)번의 합성으로 구하는 합성 관계

    \[R^n = \begin{cases} & R &, n = 1\\ &R^{n-1} \circ R &, n \gt 1\\ \end{cases}\]
    • 추이관계와 거듭제곱의 관계: 관계 \(R\)이 추이관계일 필요충분조건은 모든 양의 정수 \(n\)에 대하여 \(R^n \subseteq R\)

5. 관계의 폐포

  • 관계의 폐포(closure): 집합 \(A\)에 대한 관계 \(R\)이 가져야 하는 성질 \(P\)가 있을 때, \(R\)을 포함하면서 \(P\)를 갖는 집합 \(A\)에 대한 관계 \(S\)
  • 반사폐포(reflexive closure): 집합 \(A\)에 대한 관계 \(R\)을 포함하면서 반사 관계인 관계 \(S\), \(S = R \cup \{(a, a) \mid a \in A\}\)
  • 대칭폐포(symmetric closure): 집합 \(A\)에 대한 관계 \(R\)을 포함하면서 대칭 관계인 관계 \(S\), \(S = R \cup \{(b, a) \in A \times A \mid (a, b) \in R\} = R \cup R^{-1}\)
  • 추이폐포(transitive closure): 집합 \(A\)에 대한 관계 \(R\)을 포함하면서 추이 관계인 관계 \(S\), \(S = R \cup \{(a, c) \mid (a, b) \in R \land (b, c) \in R\}\)
    • 연결 관계(connectivity relation: \(R^*\)): \(R^* = \cup^\infty_{n=1}R^n = R^1 \cup R^2 \cup R^3 \cup \cdots\)
      • 일반적으로 \(M_R\)의 크기가 \(n\)일 때, \(R\)의 연결 관계 \(R^* = \cup^n_{k=1}R^k\)
    • 연결 관계와 추이폐포의 관계: \(R\)의 연결 관계 \(R^*\)는 \(R\)의 추이폐포

동치 관계와 부분순서 관계

  • 동치 관계(equivalence relation): 반사, 대칭, 추이 관계가 모두 성립하는 관계

    • 동치류(equivalence class, \([a]\)): \(R\)이 동치 관계일 때, 집합 \(A\)의 원소 \(a\)와 순서쌍을 이루는 원소들의 집합, \([a] = \{x \mid (a, x) \in R\}\)
    • 동치류 집합 \(S = \{A_1, A_2, \cdots, A_k\}\)의 특징
      • \(i = 1, 2, \cdots, k\)일 때, \(A_i \neq \varnothing\)
      • $A_i \subseteq A$$
      • \(i \neq j\)이면, \(A_i \cap A_j = \varnothing\)

  • 부분순서 관계(partial order relation): 반사, 반대칭, 추이 관계가 성립하는 관계

    • 부분순서 집합(partial order set): 집합 \(A\)에 대한 관계 \(R\)이 부분순서 관계이면, \(A\)는 부분순서 집합
    • 비교 가능(comparable): 집합 \(A\)에 대한 관계 \(R\)이 부분순서 관계이고 \((a, b) \in R\) 또는 \((b, a) \in R\)인 경우, \(a\)와 \(b\)는 비교 가능
      • \((a, b) \in R\)인 경우: \(a \leqslant b\)
      • \((b, a) \in R\)인 경우: \(b \leqslant a\)
    • 비교 불가능(noncomparable): 집합 \(A\)에 대한 관계 \(R\)이 부분순서 관계이고 \((a, b) \notin R\) 또는 \((b, a) \notin R\)인 경우, \(a\)와 \(b\)는 비교 불가능
      • \((a, b) \notin R\)인 경우: \(a \nleqslant b\)
      • \((b, a) \notin R\)인 경우: \(b \nleqslant a\)

  • 완전순서 관계(total order relation): 집합 \(A\)에 대한 관계 \(R\)이 부분순서 관계일 때, \(A\)의 모든 원소가 \(R\)에서 비교 가능하면 \(R\)을 완전순서 관계라 하고, \(A\)를 완전순서 집합이라고 함

  • 하세도표(Hasse diagram): 부분순서 관계의 특징을 적용한 표기 방법

    1. 방향그래프에서 루프 생략
    2. \(a \neq b\)인 부분순서 집합의 원소 \(a, b \in A\)에 대하여 \((a, b) \in R\)이면 정점 \(a\)를 정점 \(b\)보다 아래쪽에 그림
    3. \(a \neq b \neq c\)인 부분순서 집합의 원소 \(a, b, c \in A\)에 대하여, \((a, b) \in R\), \((b, c) \in R\), \((a, c) \in R\)일 때, 정점 \(a\)에서 정점 \(c\)로 가는 선만 그리고, 정점 \(a\)에서 정점 \(b\), 정점 \(b\)에서 정점 \(c\)로 가는 선은 생략
    • 극대원소(maximal element): 부분순서 집합 \(A\)의 원소 \(a\)에 대해 \(a \lt b\)인 원소 \(b\)가 존재하지 않을 때, 원소 \(a\)​
      • 하세도표에서 최상위에 위치
    • 극소원소(minimal element): 부분순서 집합 \(A\)의 원소 \(a\)에 대해 \(a \lt b\)인 원소 \(b\)가 존재하지 않을 때, 원소 \(b\)
      • 하세도표에서 최하위에 위치
    • 최대원소(greatest element): 부분순서 집합 \(A\)의 모든 원소 \(a\)에 대해 \(a \leqslant b\)인 원소 \(b\)​
      • 하세도표에서 최상단에 위치하는 단 하나의 원소
    • 최소원소(least element): 부분순서 집합 \(A\)의 모든 원소 \(a\)에 대해 \(a \leqslant b\)인 원소 \(a\)
      • 하세도표에서 최하위에 위치하는 단 하나의 원소
Math, Discrete Mathematics
discrete
This post is licensed under CC BY 4.0 by the author.