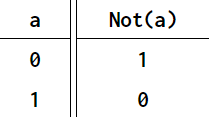이산수학 7. 부울대수
1. 부울대수의 개념
- 부울대수(Boolean algebra) / 논리대수(logic algebra): 이진의 값인 부울값(0 or 1)을 이용해 논리 동작을 표현하는 대수
- 부울값(Boolean value): 디지털신호, 0 또는 1
- 부울변수(Boolean variable): 부울값을 받는 변수
- 부울함수(Boolean function, \(n\)차 부울함수): \(n\)개의 부울변수와 연산자로 구성된 식
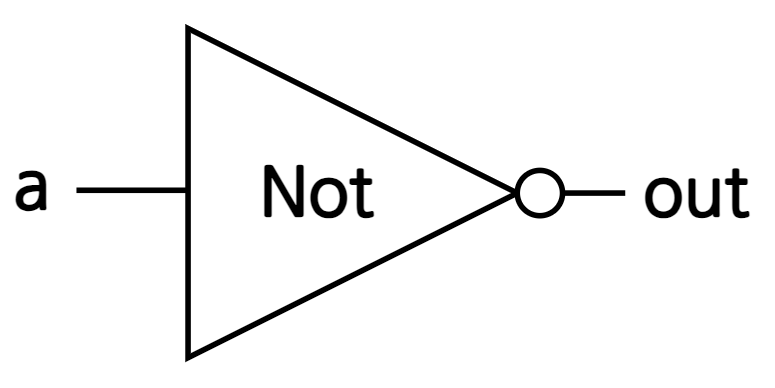
- 부울보수(Boolean complement, \(A^\prime\) 또는 \(\bar{A}\)): 부울변수의 값을 반전시키는 단항 연산자
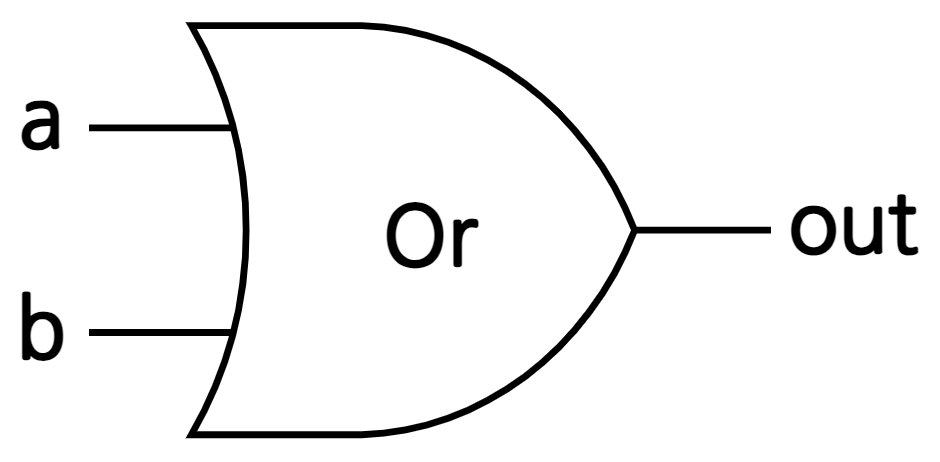
- 부울합(Boolean addition, \(A + B\)): 부울변수의 값을 더하는 이항연산자, or 연산
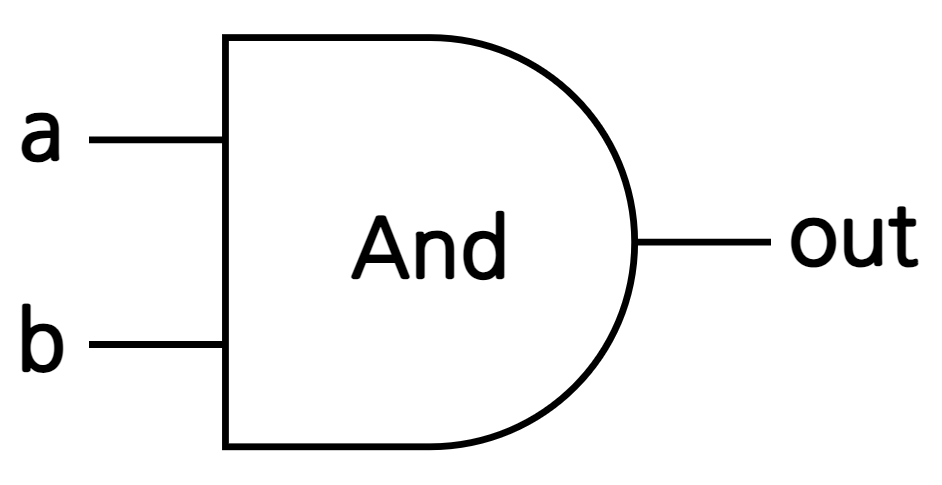
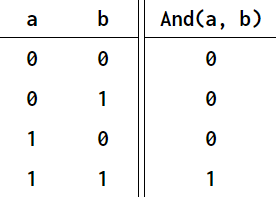
- 부울곱(Boolean multiplication, \(A \cdot B\)): 부울변수의 값을 곱하는 이항연산자, and 연산
2. 부울함수의 표현
- 리터럴(literal): 부울변수와 부울보수 연산을 한 부울변수 모두를 부르는 말
- 예) \(f(x, y) = x + y\), 리터럴: \(x\), \(\bar{x}\), \(y\), \(\bar{y}\)
- 정규항(normal form)
- 논리합 정규항(DNF, Disjunctive Normal form): 부울곱으로 연산된 항을 부울합으로 연산하는 함수 형태
- 예) \(f(x, y) = x\bar{y} + \bar{x}y\)
- 논리곱 정규항(CNF, Conjunctive Normal form): 부울합으로 연산된 항을 부울곱으로 연산하는 함수 형태
- 예) \(f(x, y) = (x + \bar{y})(\bar{x} + y)\)
- 논리합 정규항(DNF, Disjunctive Normal form): 부울곱으로 연산된 항을 부울합으로 연산하는 함수 형태
- 최소항(minterm): DNF인 \(n\)차 부울함수를 구성하는 항들 중 리터럴 \(n\)개의 부울곱으로 구성된 항
- 최소항 전개: DNF인 부울함수를 구성하는 모든 항이 최소항으로 전개된 형태
- 최대항(maxterm): CNF인 \(n\)차 부울함수를 구성하는 항들 중 리터럴 \(n\)개의 부울합으로 구성된 항
- 최대항 전개: CNF인 부울함수를 구성하는 모든 항이 최대항으로 전개된 형태
- 카르노맵(Karnaugh map): 부울함수를 단순화하기 위해 부울변수의 상호관계를 표현한 표
- 각 경우(행, 열 제목)를 적을 때 한 비트씩 차이나도록 적어야 함
- 예) 00 01 11 10(O), 00 01 10 11(X, 01과 10은 두 비트 다름)
- 카르노맵을 이용한 간략화 방법
- 부울함수의 진리표 작성
- 진리표를 최소합으로 표현
- 최소합을 바탕으로 카르노맵 작성(해당하는 항만 1로 표시)
- 상하좌우 인접(마지막과 처음도 인접으로 생각)한 1을 \(2^n, 2^{n-1}, ... 2\)개씩 순서대로 묶음(최대한 크게 묶는 것이 좋음)
- 묶은 결과에서 꼭 필요한 변수만 모아 논리합으로 전개
- 각 경우(행, 열 제목)를 적을 때 한 비트씩 차이나도록 적어야 함
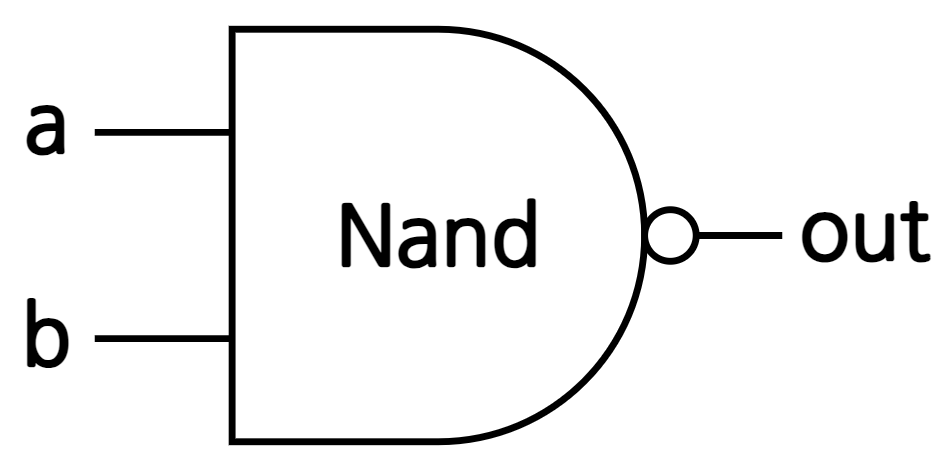
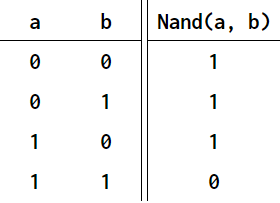
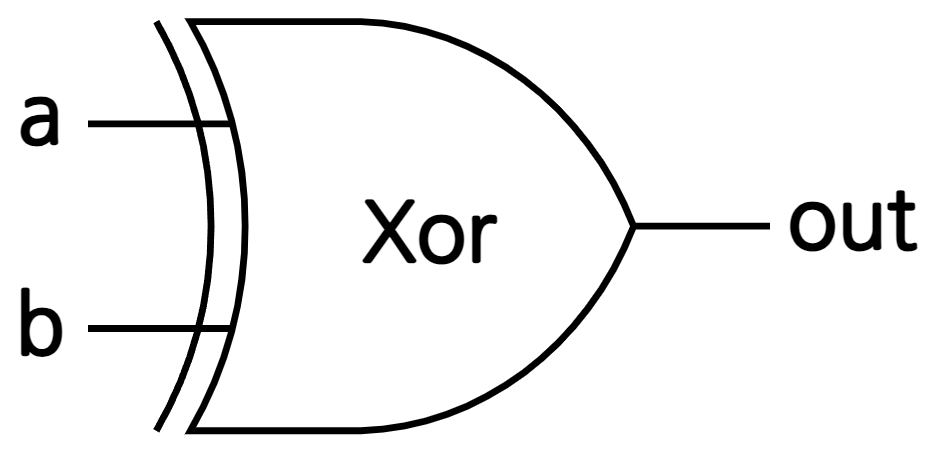
3. 논리 게이트
This post is licensed under CC BY 4.0 by the author.