선형대수학 for Graphics Chapter 1. 벡터와 포인트

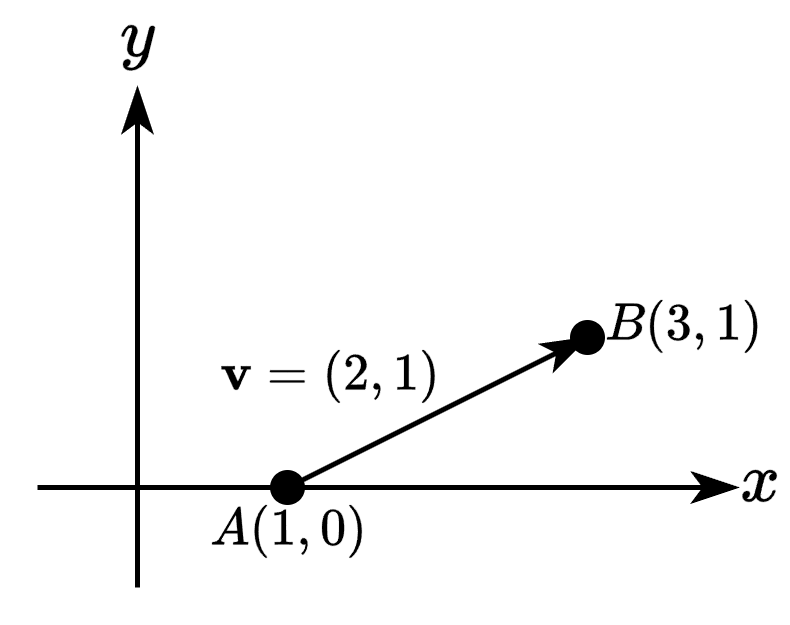
벡터(vector)

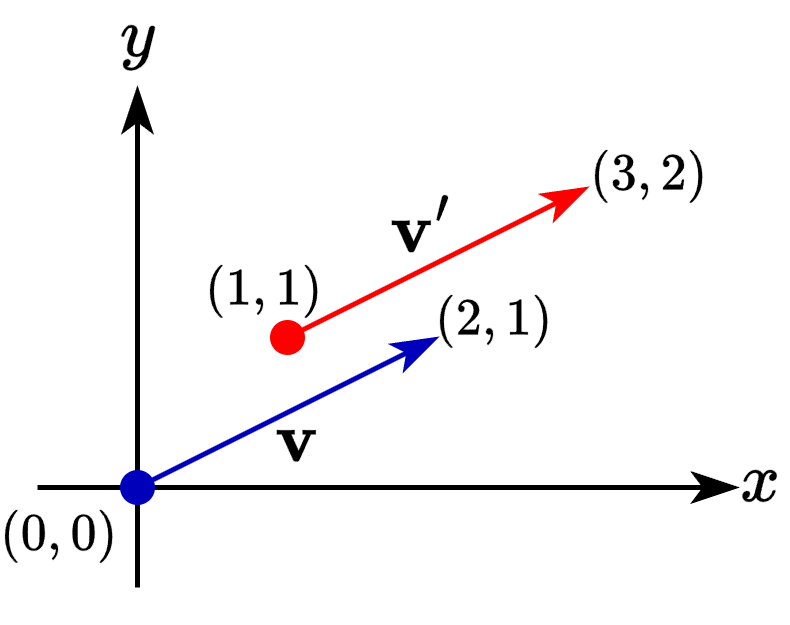
• 방향과 크기(길이)만을 갖는 물리량
  • 굵은 글씨체를 이용해 표기: \(\mathbf{v}\)​
  • 그림으로 나타낼 때는 화살표
  • 원점에서 \(\mathbf{a}\)가 \(x\)축으로는 1, \(y\)축으로는 2만큼 떨어져 있다면 \(\mathbf{a} = (1, 2)\)처럼 나타냄

  • 위치는 포함하지 않음

    

    • 따라서 \(\mathbf{v}\)와 \(\mathbf{v}^\prime\)​은 같은 벡터
• 벡터의 방향
  • 원점을 기준으로 어느 곳을 향하는지 나타냄
  • \(\mathbf{a} = (1, 2)\)이면 원점에서 \((1, 2)\)를 가리킨다는 의미
• 벡터의 크기(길이)
  • 일반적으로 피타고라스의 정리를 이용해 계산
  • $\left\Vert\mathbf{v}\right\Vert=\sqrt{v_x^2 +v_y^2}$
    • \(\mathbf{a} = (1, 2)\)이면 원점에서 \(\left\Vert\mathbf{a}\right\Vert=\sqrt{1^2+2^2}=\sqrt{5}\)만큼 떨어져 있음
• 단위 벡터(unit vector): 크기가 1인 벡터
  • \(\hat{\mathbf{v}}\)처럼 hat 기호를 이용해 표기
  • 방향만을 나타내기 위해 사용

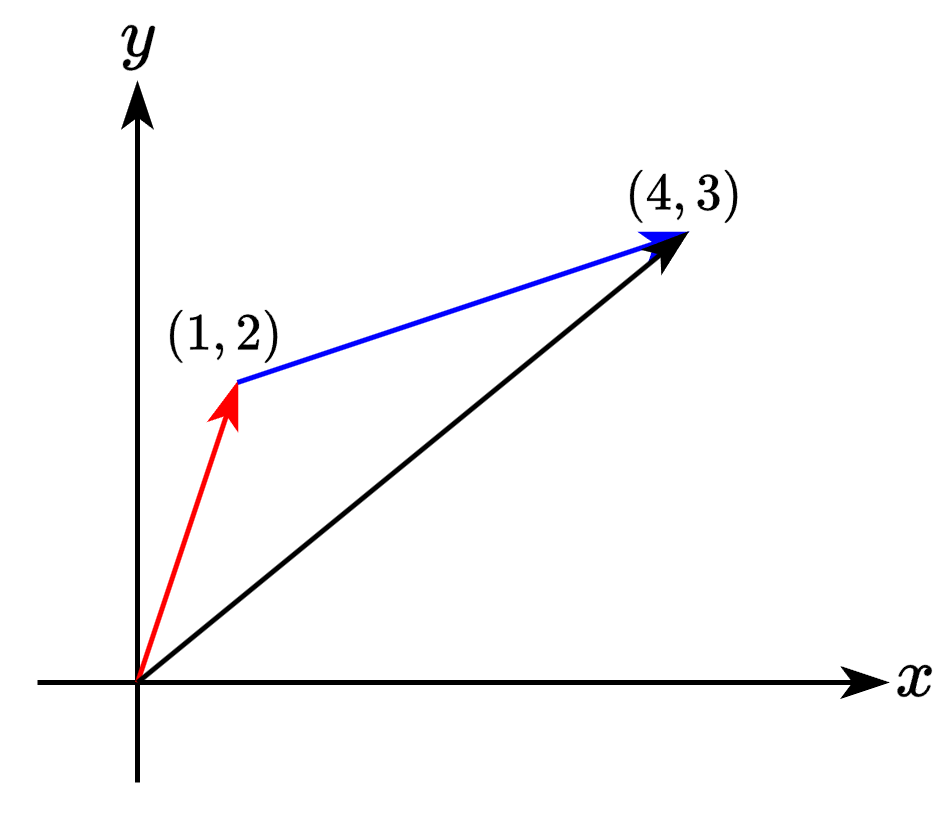
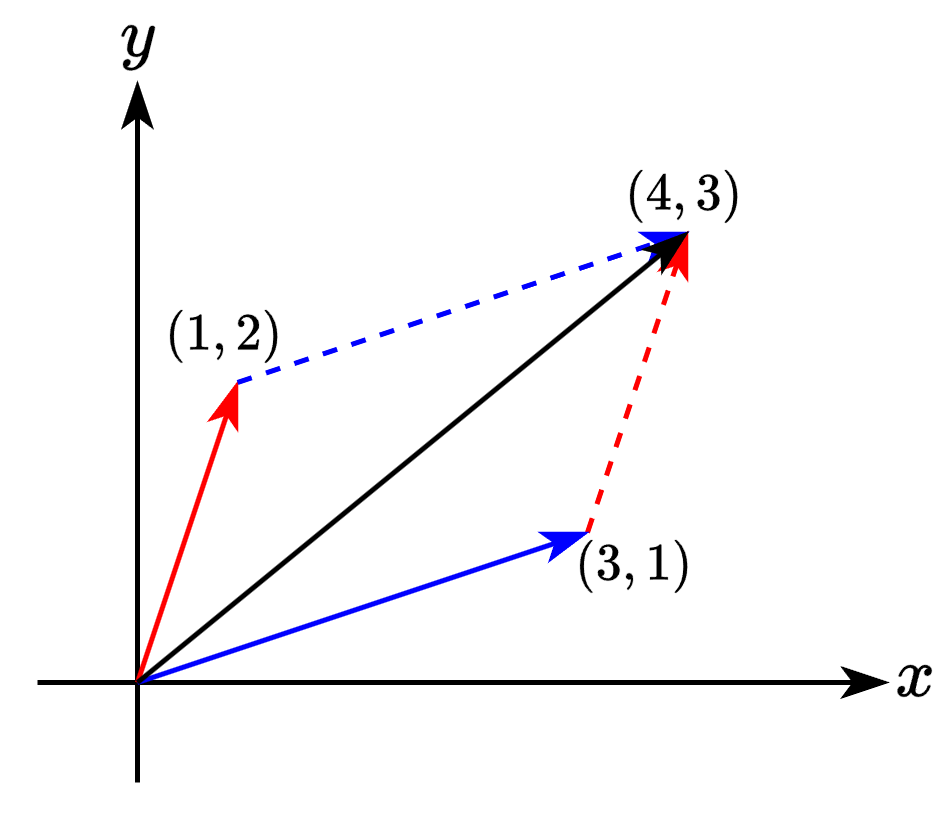
벡터의 합

• 각 원소끼리 덧셈
  • 예) \((1, 2) + (3, 1) = (4, 3)\)

• 기하적으로는 두 벡터를 연결해 새로운 벡터를 생성하는 것(삼각형법)

  

  • 다른 방법으로는 평행사변형법이 있음

    

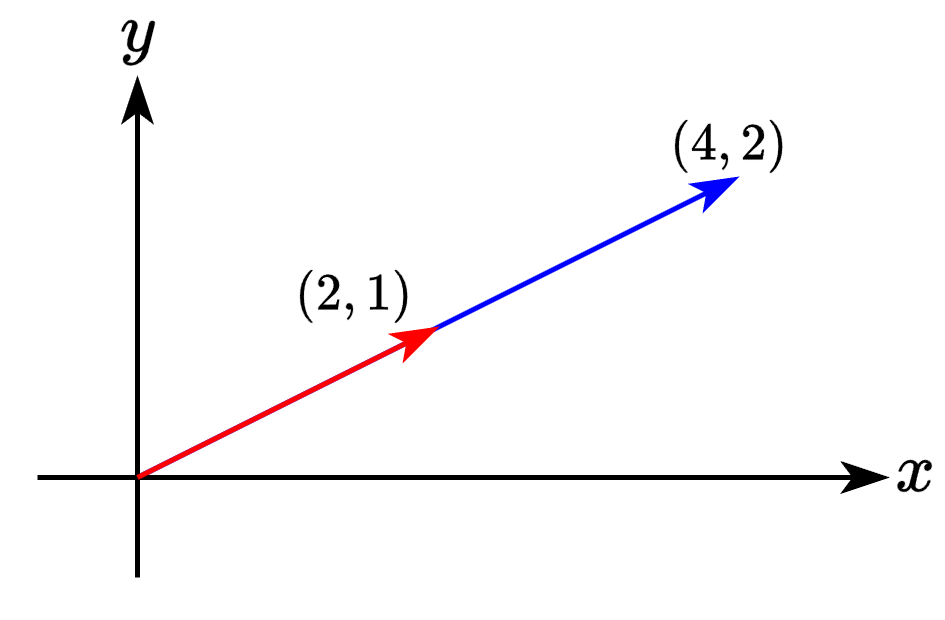
벡터의 스칼라 곱

• 스칼라: 크기 정보만 가지는 값
• 스칼라 값을 각 원소에 곱셈
  • 예) \((1, 2) \times 2 = (2, 4)\)

• 기하적으로 벡터의 크기를 스칼라 배하는 것

  

포인트(point)

• 말 그대로 ‘점’
• 위치를 나타냄
• \(P\)처럼 대문자로 표기

벡터와 포인트의 연산

• 벡터 + 벡터 = 벡터

  

• 포인트 + 벡터 = 포인트

  

  • $A + \mathbf{v} = B$

• 포인트 - 포인트 = 벡터

  

  • $B - A = \mathbf{v}$