선형대수학 for Graphics Chapter 2. 기저와 선형 결합

기저(basis)

• \(\mathbf{v} = (2, 3)\)은 \(\mathbf{v}\)가 \(x\)축으로 \(+2\)만큼, \(y\)축으로 \(+3\)만큼 이동한 곳을 가리킨다고 할 수 있음
• 이것을 수식으로 나타내면 \(\mathbf{v}=2(1, 0) + 3(0, 1)\)처럼 표현 가능
  • 여기서 \((1, 0)\), \((0, 1)\)​처럼 특정 벡터 공간의 근본이 되는 벡터를 기저라고 함
    • \((1, 0)\)은 \(x\)축을 나타내고 \((0, 1)\)은 \(y\)축을 나타냄
  • \((1,0)\), \((0, 1)\)뿐만 아니라 모든 벡터가 기저가 될 수 있음
• 표준 기저 벡터(standard basis vector)
  • \(\hat{\mathbf{i}}\): 일반적으로 \(x\)축을 의미, \((1, 0)\)
  • \(\hat{\mathbf{j}}\): 일반적으로 \(y\)축을 의미, \((0, 1)\)
  • 모든 벡터는 표준 기저 벡터 * 스칼라의 합으로 표현 가능
    • 예) \((2, 3) = 2\hat{\mathbf{i}} + 3\hat{\mathbf{j}}\)

선형 결합(linear combination)

• 벡터를 스칼라 * 벡터들의 합으로 나타내는 것
  • 예) \((2, 3) = 2\hat{\mathbf{i}} + 3\hat{\mathbf{j}}\)

선형 결합과 기저 벡터

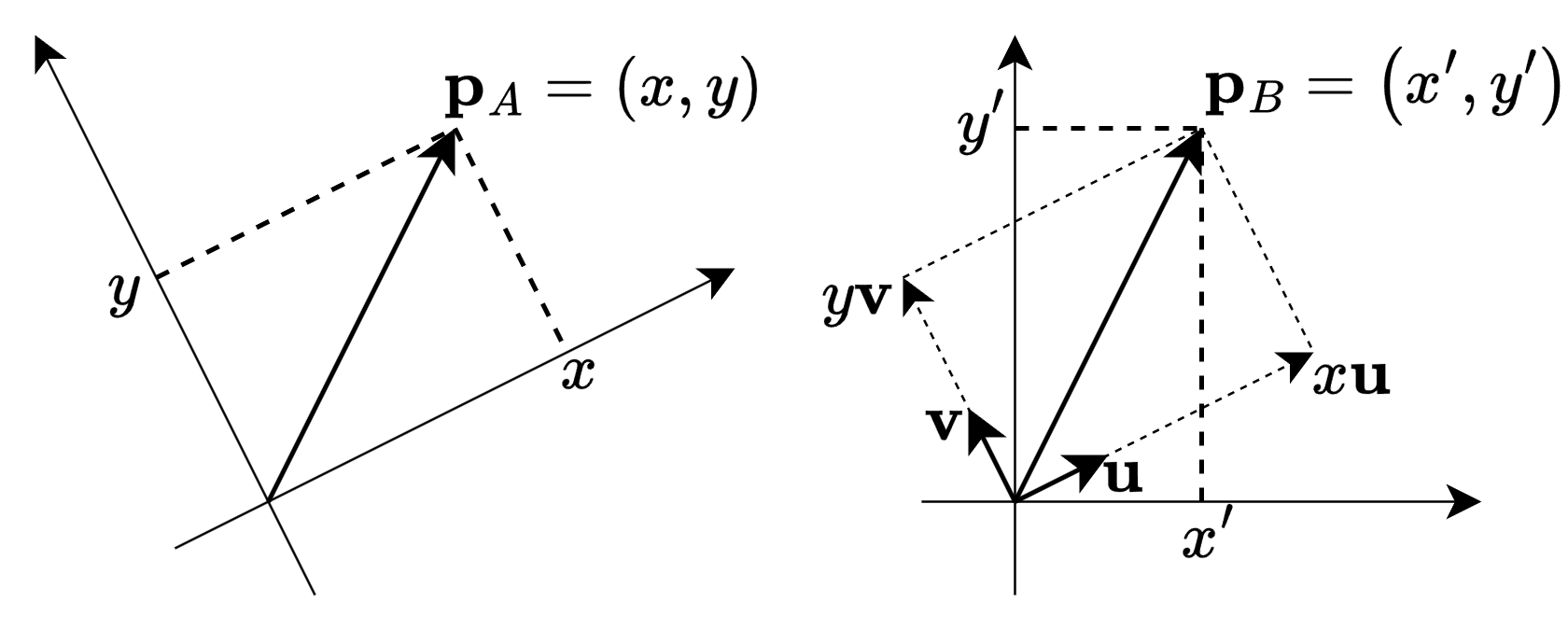
• 특정 벡터 공간에서 정의된 벡터를 표준 벡터 공간에서 알고 싶다면 해당 공간의 기저 벡터와 선형 결합을 하면 됨

• 예)

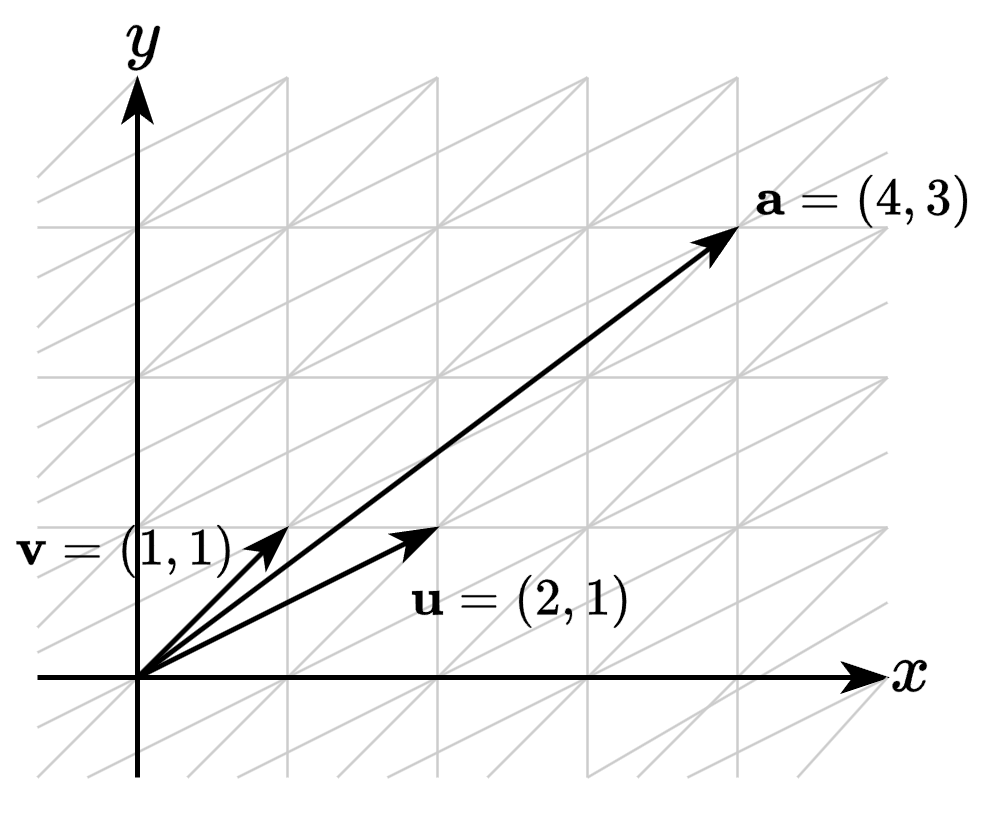
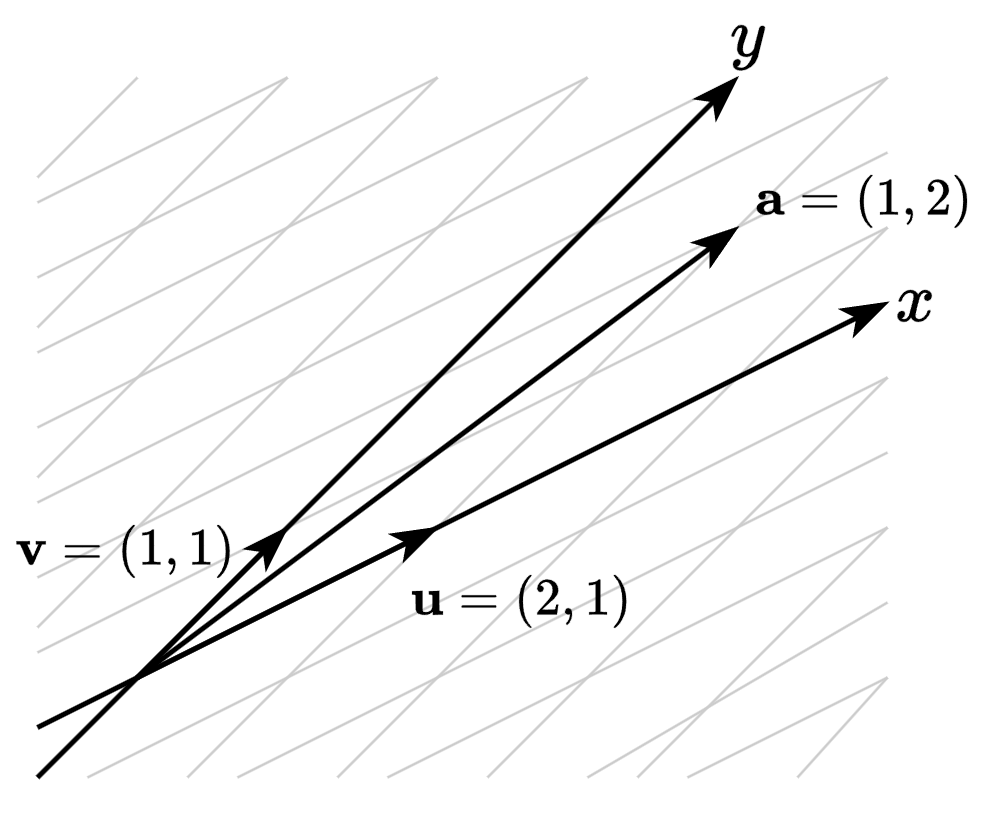  \(\mathbf{u}\)와 \(\mathbf{v}\)가 이루는 벡터 공간

  • \(x\)축을 나타내는 기저: \(\mathbf{u}=(2, 1)\)
  • \(y\)축을 나타내는 기저: \(\mathbf{v} = (1, 1)\)​
  • 벡터 \(\mathbf{u}\)와 \(\mathbf{v}\)가 이루는 벡터 공간에서 정의된 벡터 \(\mathbf{a}=(1, 2)\)​
    • \(\mathbf{u}\) 방향으로 \(+1\)만큼, \(\mathbf{v}\) 방향으로 \(+2\)​만큼 떨어진 곳을 가리키는 벡터

  표준 벡터 공간에서 표현한 \(\mathbf{a}\)

  • \(\mathbf{a}\)를 표준 기저 벡터가 이루는 공간에서 표현하고 싶다면 \(a_x\mathbf{u} + a_y\mathbf{v} = 1(2, 1) + 2(1, 1) = (4, 3)\)
  • 즉, \(\mathbf{a}\)를 표준 벡터 공간에서는 \((4, 3)\)​로 나타낼 수 있음

일반화한 그림

\[\mathbf{p}_B = (x', y') = x\mathbf{u} + y\mathbf{v}\]