선형대수학 for Graphics Chapter 3. 행렬과 선형 변환

행렬(matrix)

• 행렬: 수를 행(row)과 열(column)에 맞춰 배열한 것

  \[\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}\]
  • 3*3 형태의 행렬
• \(\mathbf{T}\): 대문자 굵은 글씨체로 표현
• 대괄호(\([]\))나 소괄호(\(()\))로 감싸 표현

• 행렬은 벡터를 나열한 것으로 생각할 수 있음

  \[\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} ,\quad \begin{bmatrix} 1\\ 4\\ 7 \end{bmatrix} \begin{bmatrix} 2\\ 5\\ 8 \end{bmatrix} \begin{bmatrix} 3\\ 6\\ 9 \end{bmatrix} ,\quad \begin{matrix} [1 & 2 & 3]\\ [4 & 5 & 6]\\ [7 & 8 & 9] \end{matrix}\]
• row-major vs column-major
  • row-major: 행을 중점으로 표기
    • 위에 식에서 3번째 경우
    • directx에서 사용하는 방식
  • column-major: 열을 중점으로 표기
    • 위에 식에서 2번째 경우
    • opengl에서 사용하는 방식

행렬의 덧셈

• 같은 위치에 있는 원소를 덧셈

  \[\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 5 & 6\\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 6 & 8\\ 10 & 12 \end{bmatrix}\]

• 따라서 모양이 다른 두 행렬은 서로 더할 수 없음

행렬의 곱셈

스칼라 곱

• 각 원소에 스칼라 값을 곱셈

  \[2\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 2 & 4\\ 6 & 8 \end{bmatrix}\]

행렬 곱

• 앞 행렬의 행과 뒤 행렬의 열을 곱셈

  \[\begin{bmatrix} a & b & c\\ d & e & f \end{bmatrix} \begin{bmatrix} a' & b'\\ c' & d'\\ e' & f' \end{bmatrix} = \begin{bmatrix} aa'+bc'+ce' & ab'+bd'+cf'\\ da'+ec'+fe' & db'+ed'+ff' \end{bmatrix}\]
• 따라서 앞 행렬의 열의 개수와 뒤 행렬의 행의 개수가 같아야 함
  • \(a\times b\) 크기의 행렬과 \(b\times c\) 크기의 행렬을 곱한 행렬의 크기는 \(a\times c\)
• 행렬 곱은 순서가 바뀌면 결과가 달라지거나 모양이 달라 곱할 수 없음

전치 행렬(transpose)

• 행렬의 행과 열을 교환한 행렬
  • 위첨자 \(T\)를 이용해 표기
    • 예) \(\mathbf{A}^T\)
  • \(y=-x\) 그래프(주 대각선)를 기준으로 뒤집은 형태
  \[\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{bmatrix}^T = \begin{bmatrix} 1 & 4\\ 2 & 5\\ 3 & 6 \end{bmatrix}\]

항등 행렬(identity)

\[\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}\]

• 주 대각 성분이 1이고 나머지는 0인 정사각행렬
• \(\mathbf{I}\)로 표기
• \(\mathbf{I} \times \mathbf{A}\)는 언제나 \(\mathbf{A}\)​

역행렬(inverse)

• 행렬과 곱했을 때 항등 행렬이 되는 행렬
  • \[\mathbf{A}\mathbf{A}^{-1}=\mathbf{I}\]
• 위첨자 \(-1\)를 이용해 표기
  • 예) \(\mathbf{A}^{-1}\)

선형 변환(linear transformation)

• 선형 변환: 벡터 공간을 다른 벡터 공간으로 변환하며 다음 조건을 만족하는 함수

\[\begin{align*}&\tau(\mathbf{u}+\mathbf{v})=\tau(\mathbf{u})+\tau(\mathbf{v})\\&\tau(k\mathbf{u})=k\tau(\mathbf{u})\end{align*}\]

• 위 조건을 만족하면 $\tau$는 선형 변환

• 선형 변환이 아닌 경우

  \[\tau(x, y, z)=(x^2, y^2, z^2)\]
  • 위의 경우 두 조건 모두 만족하지 않음
  • 따라서 선형 변환이 아님

선형 변환과 벡터 공간

• 선형 변환의 조건
  • 선형 변환 전 벡터 공간과 후 벡터 공간의 원점은 일치해야 함
  • 선형성(직선)이 유지되어야 함
• 벡터 공간 자체를 변형시킨다고 볼 수 있음

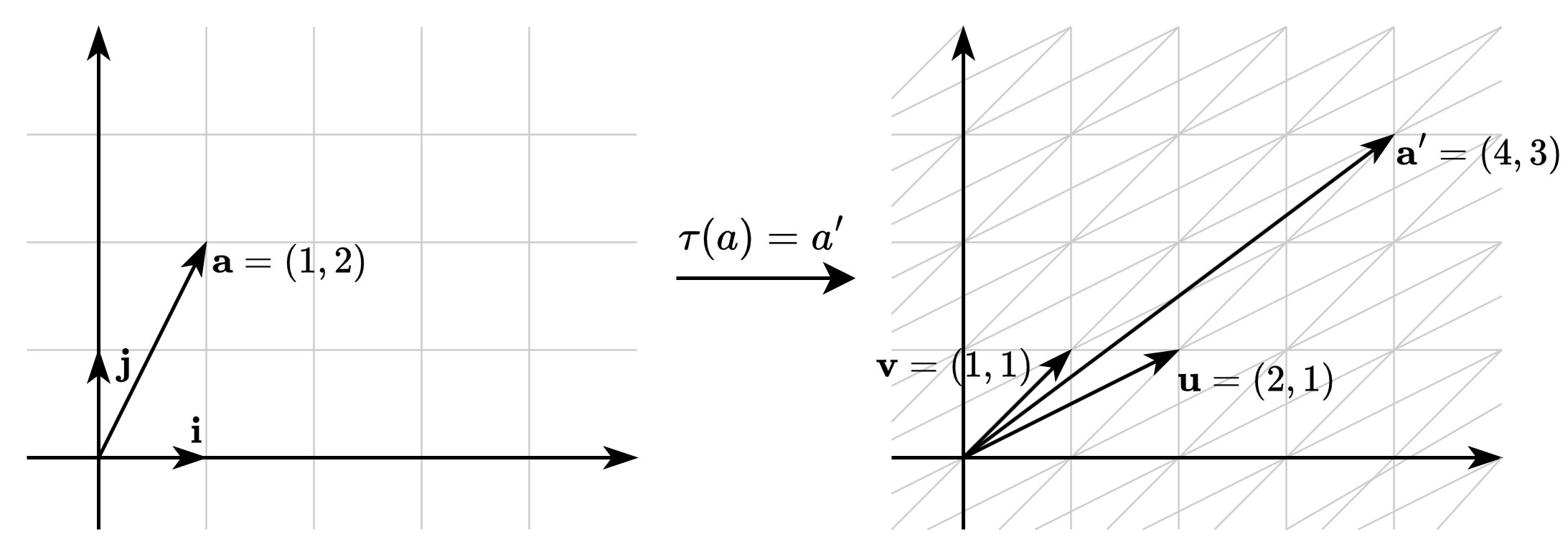
  • 예)

    

    • \(\mathbf{i}\)를 \((2, 1)\)로, \(\mathbf{j}\)를 \((1, 1)\)로 변환하는 선형 변환 \(\tau\)
    • 그림처럼 공간을 변형시켜 \(\mathbf{a}\)를 변형

  • 기저를 같은 방향이나 \(180^\circ\) 반대 방향으로 변형하는 선형 변환의 경우 공간이 직선으로 축소됨

    • 벡터 공간 내의 모든 벡터는 기저들의 선형 결합으로 나타남
    • 하지만 기저가 같은 방향이거나 반대 방향이면 선형 결합을 통해 다른 방향이 나올 수 없음
    • 만약 기저가 \((1, 0)\), \((-1, 0)\)이라면 선형 결합을 통해 생성된 벡터의 \(y\) 값은 항상 0

• \(\mathbf{i}\)를 \((1, 2)\)로, \(\mathbf{j}\)를 \((3, 0)\)으로 변환하는 선형 변환의 경우

  \[(x', y') = x(1, 2) + y(3, 0) = (x + 3y, 2x)\]
  • 위와 같이 변형된 벡터 공간에 속하는 벡터가 어떻게 변하는지 알 수 있음

변환 행렬

\[(x', y') = x(1, 2) + y(3, 0) = (x + 3y, 2x)\]

• 위 식을 행렬로 간단하게 표현할 수 있음

  \[[x, y] \begin{bmatrix} 1 & 2\\ 3 & 0 \end{bmatrix} = [x + 3y, 2x]\]

• 정리하면 \(\mathbf{i}\)를 \((1, 2)\)로, \(\mathbf{j}\)를 \((3, 0)\)으로 변환하는 선형 변환 \(\tau\)를 행렬(row-major)로 표현하면

  \[\begin{bmatrix} \leftarrow & \tau(\mathbf{i}) & \rightarrow\\ \leftarrow & \tau(\mathbf{j}) & \rightarrow \end{bmatrix}\]
  • 위와 같이 행으로 쌓는 형태
• 이처럼 선형 변환을 계산하는 행렬을 변환 행렬이라함
• 만약 row-major 변환 행렬을 column-major로 바꾸고 싶다면 전치 행렬을 구하면 됨

변환

• 기본적으로 모든 변환은 공간을 변형시키는 것이라 이해하면 편함
• 벡터를 회전시키고 싶다면?
  • 벡터가 포함된 벡터 공간을 회전시키려면 어떻게 해야할지 고민
  • 예)
    • 시계방향으로 \(90^\circ\)회전: \(\mathbf{i}\)를 \((0, -1)\)로, \(\mathbf{j}\)를 \((1, 0)\)으로 변환
• 벡터의 크기를 조절하고 싶다면?
  • 벡터가 포함된 벡터 공간의 크기를 조절하려면 어떻게 해야할지 고민
  • 예)
    • \(x\)방향으로 2배, \(y\)방향으로 3배: \(\mathbf{i}\)를 \(2\mathbf{i}\)로, \(\mathbf{j}\)를 \(3\mathbf{j}\)로 변환

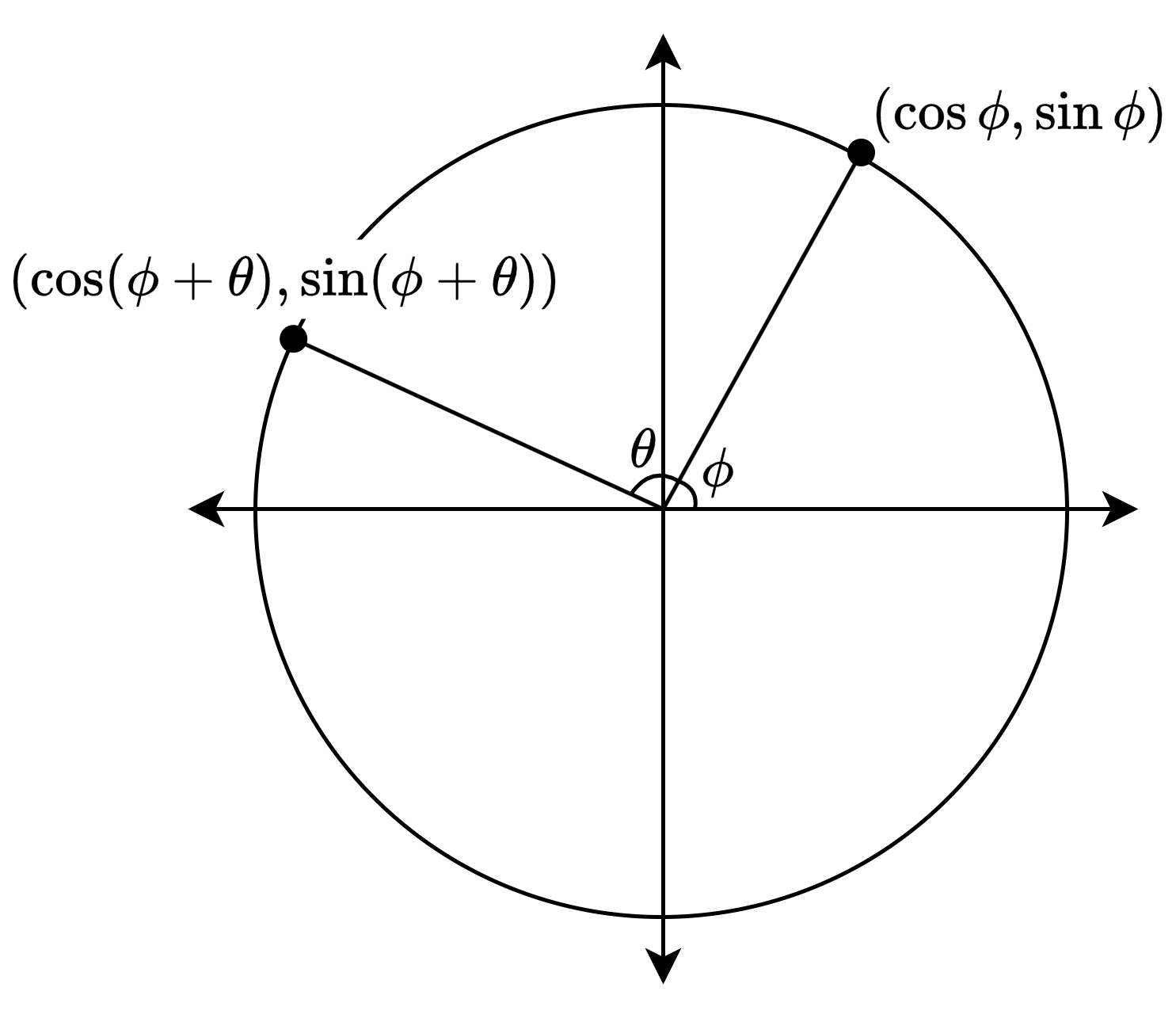
회전(2d)

\[\begin{align*}&x^\prime=x\cos{\theta}-y\sin{\theta}\\ & y^\prime=x\sin{\theta}+y\cos{\theta}\end{align*}\]

• 회전은 선형 변환

  \[\begin{align*} \text{Function:}\quad&\tau(x, y) = (x \cos\theta - y \sin\theta, x \sin\theta + y \cos\theta) \\ \text{Additivity:} \quad &\tau(u_1 + v_1, u_2 + v_2) \\ &= ((u_1 + v_1) \cos\theta - (u_2 + v_2) \sin\theta, (u_1 + v_1) \sin\theta + (u_2 + v_2) \cos\theta) \\ &= (u_1 \cos\theta - u_2 \sin\theta + v_1 \cos\theta - v_2 \sin\theta, u_1 \sin\theta + u_2 \cos\theta + v_1 \sin\theta + v_2 \cos\theta) \\ &= \tau(u_1, u_2) + \tau(v_1, v_2) \\ \text{Homogeneity:} \quad &\tau(ku_1, ku_2) \\ &= (ku_1 \cos\theta - ku_2 \sin\theta, ku_1 \sin\theta + ku_2 \cos\theta) \\ &= k(u_1 \cos\theta - u_2 \sin\theta, u_1 \sin\theta + u_2 \cos\theta) \\ &= k \tau(u_1, u_2) \end{align*}\]

• 따라서 변환 행렬(row-major)을 만들 수 있음

\[\left[x^\prime , y^\prime \right] = \left[ x, y \right]\left[\begin{matrix}\cos{\theta} & \sin{\theta}\\ -\sin{\theta} & \cos{\theta}\end{matrix}\right]\]

회전(3d)

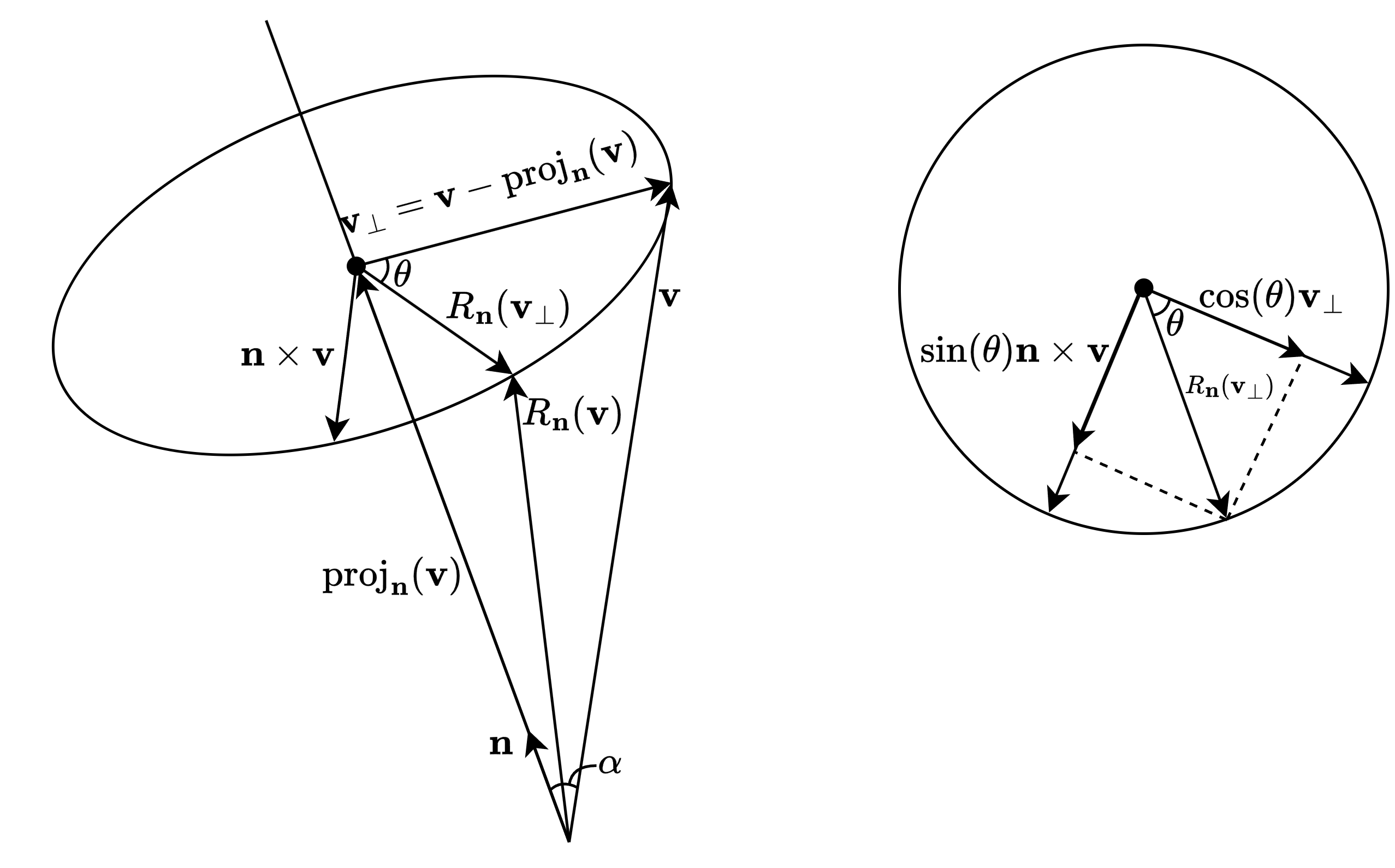
• \(\mathbf{n}\): 회전축, 단위 벡터
• \(\mathbf{v}\): 회전시킬 벡터
• \(R_\mathbf{n}\): \(\mathbf{n}\)을 기준으로 회전시키는 함수
  • 이를 수행하는 행렬을 찾는 것이 목표
• 회전 과정
  1. $\text{proj}_\mathbf{n}(\mathbf{v})=(\mathbf{n}\cdot\mathbf{v})\mathbf{n}$
  2. \(\mathbf{v}*\bot=\mathbf{v}-\text{proj}*\mathbf{n}(\mathbf{v})\): \(\mathbf{v}\)에 수직(perpendicular)한 벡터
  3. \(\mathbf{n}\times\mathbf{v}\): \(\mathbf{v}_\bot\)과 수직이며 길이가 같음
     • $\left\Vert\mathbf{n}\times\mathbf{v}\right\Vert=\left\Vert\mathbf{n}\right\Vert\left\Vert\mathbf{v}\right\Vert\sin{\alpha}=\left\Vert\mathbf{v}_\bot\right\Vert$
  4. $R_\mathbf{n}(\mathbf{v}\ast\bot)=\cos\theta\mathbf{v}\ast\bot+\sin\theta(\mathbf{n}\times\mathbf{v})$
  5. $R_\mathbf{n}(\mathbf{v})=\text{proj}\ast\mathbf{n}(\mathbf{v})+R\ast\mathbf{n}(\mathbf{v}_\bot)$
• 변환 행렬
  • Rodrigues’ rotation formula(로드리게스 회전 공식)
  \[\begin{align*}R_\mathbf{n}(\mathbf{v})&=\text{proj}*\mathbf{n}(\mathbf{v})+R*\mathbf{n}(\mathbf{v}*\bot)\\&=(\mathbf{n}\cdot\mathbf{v})\mathbf{n}+\cos\theta\mathbf{v}*\bot+\sin\theta(\mathbf{n}\times\mathbf{v})\\&=(\mathbf{n}\cdot\mathbf{v})\mathbf{n}+\cos\theta(\mathbf{v}-(\mathbf{n}\cdot\mathbf{v})\mathbf{n})+\sin\theta(\mathbf{n}\times\mathbf{v})\\&=\cos\theta\mathbf{v}+(1-\cos\theta)(\mathbf{n}\cdot\mathbf{v})\mathbf{n}+\sin\theta(\mathbf{n}\times\mathbf{v})\end{align*}\]
  • 표준 기저 벡터 대입(\(c=\cos\theta\), \(s=\sin\theta\))
  \[R_\mathbf{n} = \begin{bmatrix} \leftarrow&R_\mathbf{n}(\mathbf{i})&\rightarrow\\ \leftarrow&R_\mathbf{n}(\mathbf{j})&\rightarrow\\ \leftarrow&R_\mathbf{n}(\mathbf{k})&\rightarrow \end{bmatrix} = \begin{bmatrix} c + (1-c)x^2 & (1-c)xy + sz & (1-c)xz - sy\\ (1-c)xy - sz & c + (1-c)y^2 & (1-c)yz + sx\\ (1-c)xz + sy & (1-c)yz - sx & c + (1-c)z^2 \end{bmatrix}\]
  • \(\mathbf{n}\)이 \(x\)축인 경우(\(x=1, y=0, z=0\))
  \[R_\mathbf{x} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & \sin\theta \\ 0 & -\sin\theta & \cos\theta \end{bmatrix}\]
  • \(\mathbf{n}\)이 \(y\)축인 경우(\(x=0, y=1, z=0\))
  \[R_\mathbf{y} = \begin{bmatrix}\cos\theta & 0 & -\sin\theta \\0 & 1 & 0 \\\sin\theta & 0 & \cos\theta\end{bmatrix}\]
  • \(\mathbf{n}\)이 \(z\)축인 경우(\(x=0, y=0, z=1\))
  \[R_\mathbf{z} = \begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

  • 역행렬

    \[R_\mathbf{n}^{-1}=R_\mathbf{n}^T = \begin{bmatrix}c + (1-c)x^2 & (1-c)xy - sz & (1-c)xz + sy\\(1-c)xy + sz & c + (1-c)y^2 & (1-c)yz - sx\\(1-c)xz - sy & (1-c)yz + sx & c + (1-c)z^2\end{bmatrix}\]
    • 회전 변환 행렬의 역변환 행렬은 전치 행렬과 같음

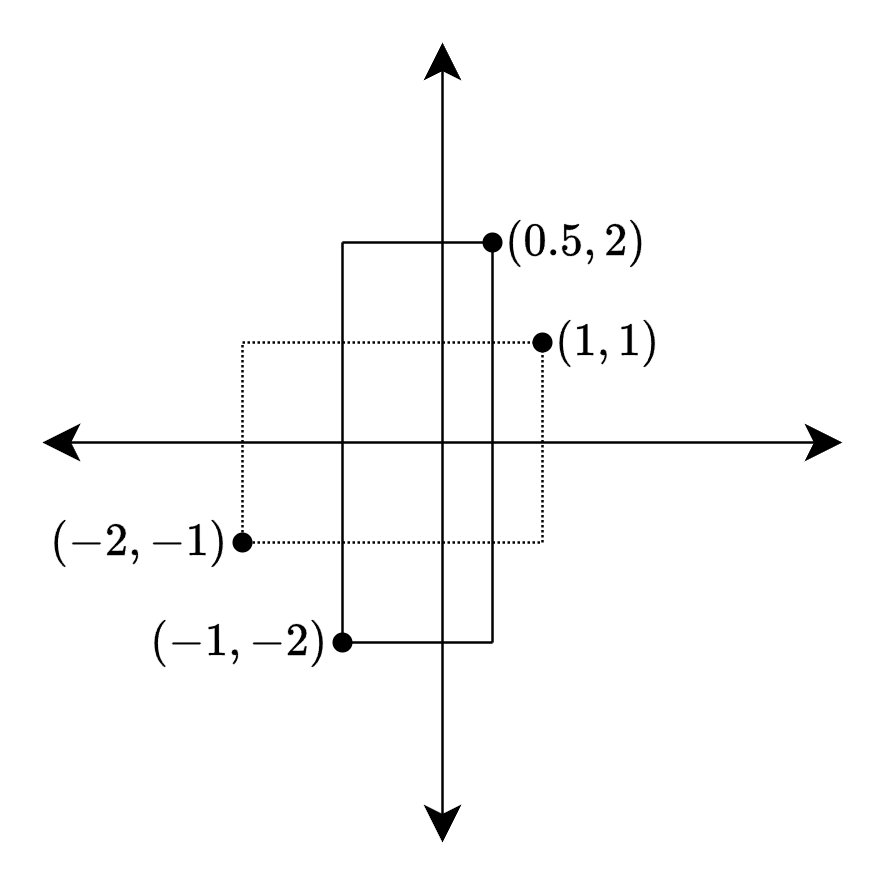
스케일링(scaling)

\[S(x, y, z) = (s_xx, s_yy, s_zz)\]

• \(x\)방향으로는 \(s_x\)만큼, \(y\)방향으로는 \(s_y\)만큼, \(z\)방향으로는 \(s_z\)만큼 변형

• 스케일링도 선형 변환이므로 변환 행렬을 구할 수 있음

  \[\begin{align*}&S(\mathbf{i})=(s_x\cdot1, s_y\cdot0, s_z\cdot0)=(s_x, 0, 0)\\&S(\mathbf{j})=(s_x\cdot0, s_y\cdot1, s_z\cdot0)=(0, s_y, 0)\\&S(\mathbf{k})=(s_x\cdot0, s_y\cdot0, s_z\cdot1)=(0, 0, s_z)\end{align*}\] \[\mathbf{S}=\begin{bmatrix}s_x&0&0\\0&s_y&0\\0&0&s_z\end{bmatrix}\quad\mathbf{S}^{-1}=\begin{bmatrix}1/s_x&0&0\\0&1/s_y&0\\0&0&1/s_z\end{bmatrix}\]

• 예)

  

\[\begin{align*}&\mathbf{S}=\begin{bmatrix}0.5&0\\0&2\end{bmatrix}\quad[1, 1]\begin{bmatrix}0.5&0\\0&2\end{bmatrix}=[0.5, 2]\\&\mathbf{S}^{-1}=\begin{bmatrix}2&0\\0&0.5\end{bmatrix}\quad[-1, -2]\begin{bmatrix}2&0\\0&0.5\end{bmatrix}=[-2, -1]\end{align*}\]

• \(\mathbf{S}\): 가로는 0.5배, 세로는 2배 변형시키는 변환 행렬

그 외

• \(x\)축에 대한 반사

  • \(\mathbf{i}\) 기저는 그대로, \(\mathbf{j}\) 기저는 \(-\mathbf{j}\)로 변환

    \[[x, y] \begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix} = [x, -y]\]

• \(x\)방향으로 밀기(shear)

  

  • \(\mathbf{i}\) 기저는 그대로, \(\mathbf{j}\) 기저는 \((\gamma, 1)\)​로 변환
    • \(\gamma\): shear 계수

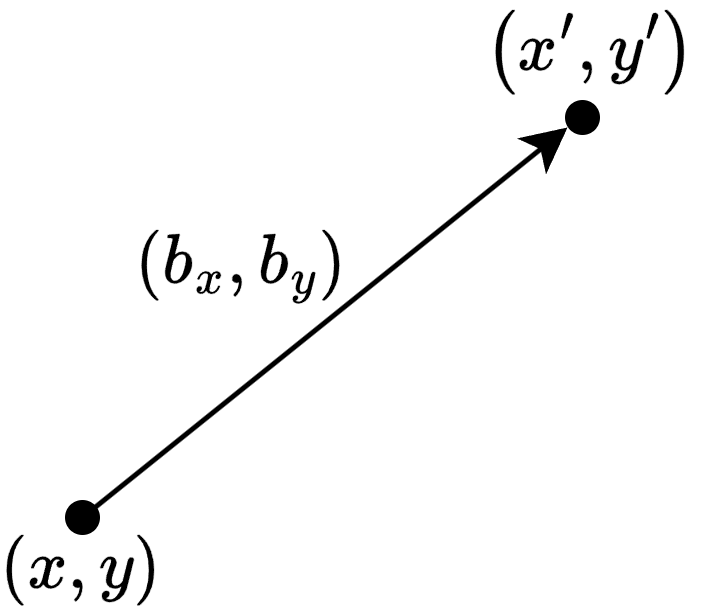
이동(transition)

\[\begin{align*}&x^\prime=x+b_x\\&y^\prime=y+b_y\end{align*}\]

• \(x\)를 \(b_x\)만큼, \(y\)를 \(b_y\)만큼 이동

• 이동은 회전, 스케일링과 달리 선형 변환이 아님

  \[\begin{align*} \text{Function:}\quad&\tau(x, y, z) = (x + b_x, y + b_y, z + b_z) \\ \text{Homogeneity:} \quad &\tau(ku_1, ku_2, ku_3) \\ &= (ku_1 + b_x, ku_2 + b_y, ku_3 + b_z) \neq k \tau(u_1, u_2, u_3) \end{align*}\]
  • 계산해보면 두 조건 모두 만족하지 않음
  • 공간을 이동시키면 당연히 원점이 달라짐
• 애파인 변환(Affine Transpormation)을 이용하면 행렬로 표현할 수 있음

선형 변환과 행렬 곱

• 사각형을 시계방향으로 \(90^\circ\)회전시키고 크기를 2배 늘리고 싶다면?
  • 사각형을 이루는 꼭짓점 벡터 \(\mathbf{v}_0, \mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\)

  • \(\mathbf{v}_i\)에 \(90^\circ\)회전 변환 행렬(\(\mathbf{R}\))을 곱하고 크기를 2배 늘리는 변환 행렬(\(\mathbf{S}\))을 곱하면 됨

    \[[x_i, y_i] \begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix} \begin{bmatrix} 2 & 0\\ 0 & 2 \end{bmatrix} = \mathbf{v}\mathbf{R}\mathbf{S}\]

  • 위 식에 행렬 곱의 결합 법칙을 적용할 수 있음

    \[\mathbf{v}\mathbf{R}\mathbf{S}=\mathbf{v}(\mathbf{R}\mathbf{S})=\mathbf{v}\mathbf{T}\]
  • 시계방향으로 \(90^\circ\)회전시키고 크기를 2배 늘리는 새로운 변환 행렬 \(\mathbf{T}\)를 계산
  • 결론적으로 원하는 작업을 순차적으로 진행하는 대신, 변환 행렬끼리 먼저 곱해 하나의 변환 행렬을 구할 수 있음
    • 이렇게 하면 간단하고 중복되는 계산 없이 최종 변환 행렬을 한번만 구해 각 꼭짓점에 곱하면 되므로 속도가 빠름
• 아무리 많은 선형 변환을 한다고 해도 각각의 변환 행렬끼리 곱하면 결국 하나의 선형 변환이 됨

비정사각 변환 행렬

• \(n\)차원 벡터에 \(n\times n\) 형태의 변환 행렬을 곱하면 그대로 \(n\)차원 위의 벡터가 나옴
• 비정사각 변환 행렬을 이용하면 차원을 변형시킬 수 있음
  • 정확히 말하면 기저 벡터의 차원을 변형시키는 것
    • 정확히 반대가 되는 기저 벡터를 이용해 차원을 축소시키는 것은 기저의 차원을 변형시키는 것은 아님
    • 여전히 공간에 포함된 벡터는 2차원 상에서 표현됨
    • 엄밀히 말하면 방향을 “제한“한다고 할 수 있음

\[[x^\prime, y^\prime, z^\prime]=[x, y] \begin{bmatrix} a & c & e\\ b & d & f \end{bmatrix}, \quad [x^\prime]=[x, y] \begin{bmatrix} a\\ b \end{bmatrix}\]

• 위 식처럼 2차원을 3차원으로 확장시키거나 1차원으로 축소시킬 수 있음
• 일반화하면 \(n\)차원 벡터를 \(m\)차원으로 변형하고 싶다면 \(n\times m\) 형태의 행렬을 곱하면 됨(row-major)