선형대수학 for Graphics Chapter 4. 행렬식

행렬식

소행렬(minor matrix)

• 특정 원소의 행과 열을 제외한 행렬

• 예)

  \[\begin{align*}&\mathbf{\bar{A}}_{11}=\left[\begin{matrix}A_{22}&A_{23}\\A_{32}&A_{33}\end{matrix}\right]\\&\mathbf{\bar{A}}_{22}=\left[\begin{matrix}A_{11}&A_{13}\\A_{31}&A_{33}\end{matrix}\right]\\&\mathbf{\bar{A}}_{13}=\left[\begin{matrix}A_{21}&A_{22}\\A_{31}&A_{32}\end{matrix}\right]\end{align*}\]
  • \(\mathbf{\bar{A}}_{rc}\): \(r\)번째 행과 \(c\)번째 열을 제외한 소행렬

행렬식(determinant)

\[\det{\mathbf{A}}=\sum_{j=1}^n A_{1j}(-1)^{1+j}\det{\mathbf{\bar{A}}_{1j}}\]

• \(n\): 열의 개수
• \(A_{1j}\): 첫번째 행의 각 원소
• \((-1)^{1+j}\): 홀수번째 열이면 양수, 짝수번째 열이면 음수
• \(\det{\mathbf{\bar{A}}_{1j}}\): 첫번째 행의 각 원소에 대한 소행렬의 행렬식

• 예)

  \[\det{\left[\begin{matrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{matrix}\right]}=A_{11}\det{\left[A_{22}\right]}-A_{12}\det{\left[A_{21}\right]}=A_{11}A_{22}-A_{12}A_{21}\]
• 3x3 이상 행렬의 determinant는 재귀적으로 계산

행렬식의 기하학적 의미

• 어느정도 스케일링 했는지를 의미
  • \((0, 0)\), \((1, 0)\), \((1, 1)\), \((0, 1)\)로 구성
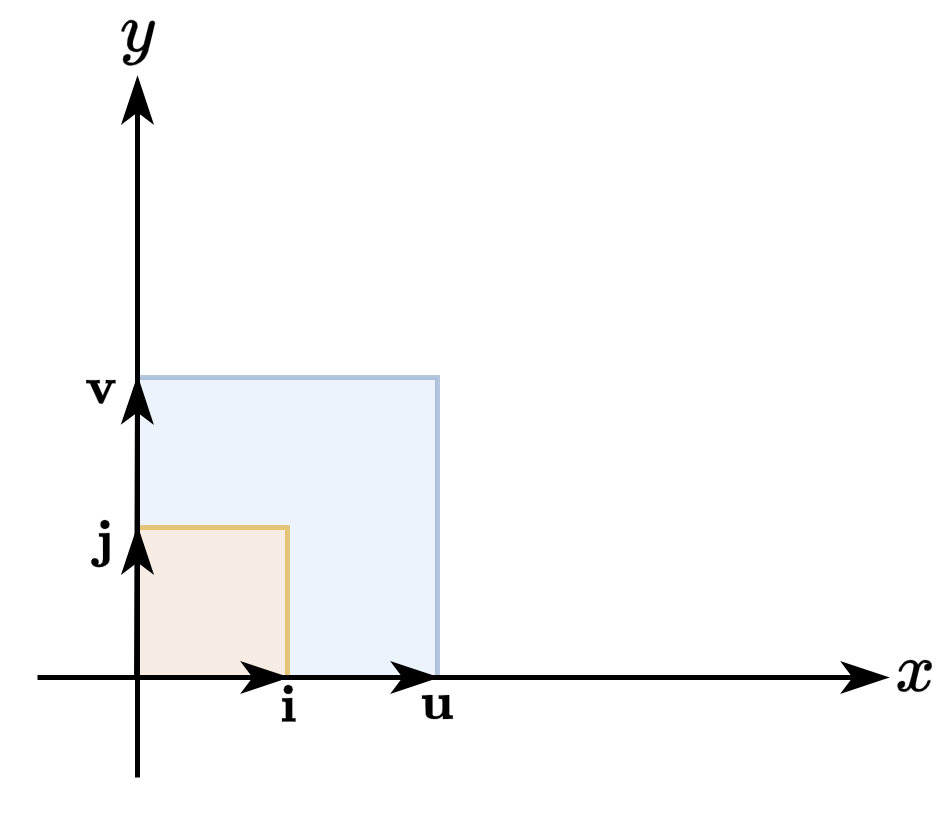
  • 2차원 정사각형의 넓이를 2배로 스케일링 하는 변환 행렬의 행렬식은 2(절대값)
  • 3차원 정육면체의 부피를 4배로 스케일링 하는 변환 행렬의 행렬식은 4(절대값)

• \(x\)축 기저를 2배, \(y\)축 기저도 2배 늘려 결과적으로 넓이를 4배 늘리는 스케일링

  • 변환 행렬

    \[\mathbf{T}=\begin{bmatrix} 2 & 0\\ 0 & 2 \end{bmatrix}\]

  • 변환 행렬의 행렬식

    \[\det\mathbf{T}=4-0=4\]

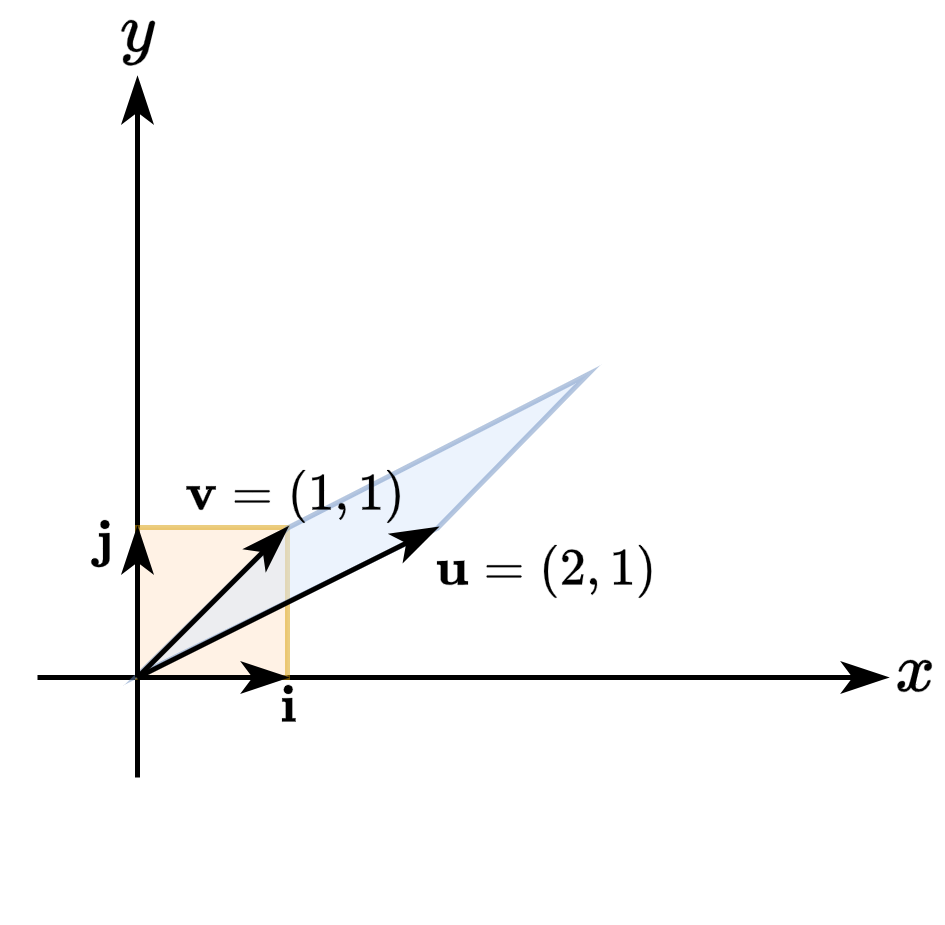
• \(x\)축 기저를 \((2, 1)\)로, \(y\)축 기저를 \((1, 1)\)로 변환

  • 변환 행렬

    \[\mathbf{T}= \begin{bmatrix} 2 & 1\\ 1 & 1 \end{bmatrix}\]

  • 변환 행렬의 행렬식

    \[\det\mathbf{T}=2-1=1\]
• 0인 경우
  • 기저 벡터의 방향이 같거나 반대, 또는 영벡터일 때
• 음수인 경우
  • 공간이 뒤집혔을 때