선형대수학 for Graphics Chapter 5. 역행렬, 랭크, 영공간

역행렬(inverse)

• 선형 변환에서 표준 공간에서의 벡터에 변환 행렬을 곱해 벡터를 변환함

  \[\mathbf{v}^\prime=\mathbf{v}\mathbf{T}\]

• 만약 변환된 벡터를 다시 표준 공간의 벡터로 변환하고 싶다면 변환 행렬의 역행렬을 이용할 수 있음

  \[\mathbf{v}^\prime\mathbf{T}^{-1}=\mathbf{v}\]
  • 변환 행렬을 역행렬을 변환된 벡터에 곱하면 표준 공간에서의 벡터로 다시 변환시킬 수 있음
  • 예)
    • 시계방향으로 \(90^\circ\) 회전시키는 변환 행렬의 역행렬: 반시계방향으로 \(90^\circ\) 회전시키는 변환행렬

• 역행렬을 구할 수 없는 경우

  • 차원을 축소시키는 경우 또는 점(모든 기저 벡터가 영 벡터)으로 변환시키는
  • 예)
    • 2차원 -> 직선
    • 3차원 -> 평면(2차원)
  • 이 경우 행렬식의 값은 0
  • 따라서 정리하면 행렬식이 0이면 역행렬을 구할 수 없음

역행렬 구하기

• 행렬식과 여인수 행렬, 수반 행렬을 이용해 구할 수 있음

• Cofactor Matrix(여인수 행렬)

  \[\mathbf{C_A}=C_{ij}=(-1)^{i+j}\det{\mathbf{\bar{A}}* {ij}}=\left[\begin{matrix} C*{11} & C_{12} & \dots & C_{1n} \\ C_{21} & C_{22} & \dots & C_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ C_{n1} & C_{n2} & \dots & C_{nn} \end{matrix}\right]\]

• Adjoint Matrix(수반 행렬) \(\mathbf{A}^\ast=\mathbf{C}_\mathbf{A}^T\)

• Inverse Matrix(역행렬) \(\mathbf{A}^{-1}=\frac{\mathbf{A}^\ast}{\det{\mathbf{A}}}\)

랭크(rank)

열, 행공간(column, row-space)

• 행렬의 열, 행들의 선형 결합으로 생성된 벡터들의 집합
• column-major라면 열공간과, row-major라면 행공간과 함께 변환 행렬을 생각할 수 있음

행공간과 변환 행렬

• 변환 행렬의 각 행은 기저 벡터에 대한 정보를 담고 있음

  \[\begin{bmatrix} \leftarrow & \tau(\mathbf{i}) & \rightarrow\\ \leftarrow & \tau(\mathbf{j}) & \rightarrow\\ \leftarrow & \tau(\mathbf{k}) & \rightarrow \end{bmatrix}\]

• 따라서 변환 행렬의 행공간, 즉 변환 행렬의 행들의 선형 결합으로 생성된 벡터는 기저의 벡터 공간과 일치

  • 예)

    \[\begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix} \rightarrow x(0, -1)+y(1, 0)\]

랭크

• 행공간 또는 열공간의 차원
  • 행공간과 열공간의 차원은 서로 같음(랭크 값이 같음)
• \(\text{rank}(\mathbf{A})\): \(\text{rank}()\) 안에 행렬을 넣어 표시

• 예)

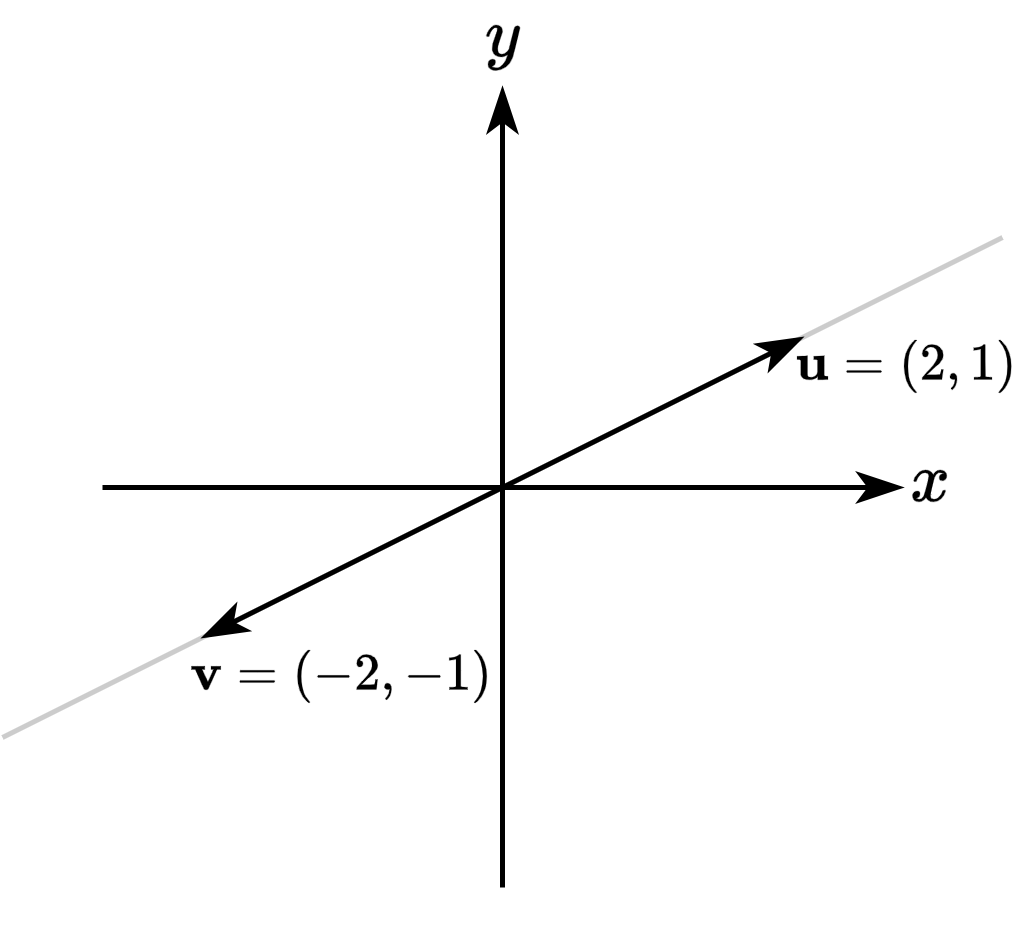
  \[\begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix}\]
  • 시계 방향으로 \(90^\circ\) 회전시키는 변환 행렬의 행공간은 2차원 전체
  • 따라서 차원은 2

  • \(\text{rank}(\mathbf{T})=2\)로 표기

    

  \[\begin{bmatrix} 2 & 1\\ -2 & -1 \end{bmatrix}\]
  • 공간을 \(y=\frac{1}{2}x\)로 축소시키는 변환 행렬의 행공간은 1차원 직선
  • 따라서 차원은 1
  • \(\text{rank}(\mathbf{T})=1\)로 표기
• \(n\)차원 공간에서의 변환 행렬의 랭크 최대값은 \(n\)
  • 만약 \(n\)보다 작다면 공간이 축소된 것이므로 행렬식이 0

영공간(null-space) 또는 커널(kernel)

• 선형 변환에 의해 영벡터가 되는 벡터들의 집합
  • \(\mathbf{v}\mathbf{A}=0\)(row-major)

• 예)

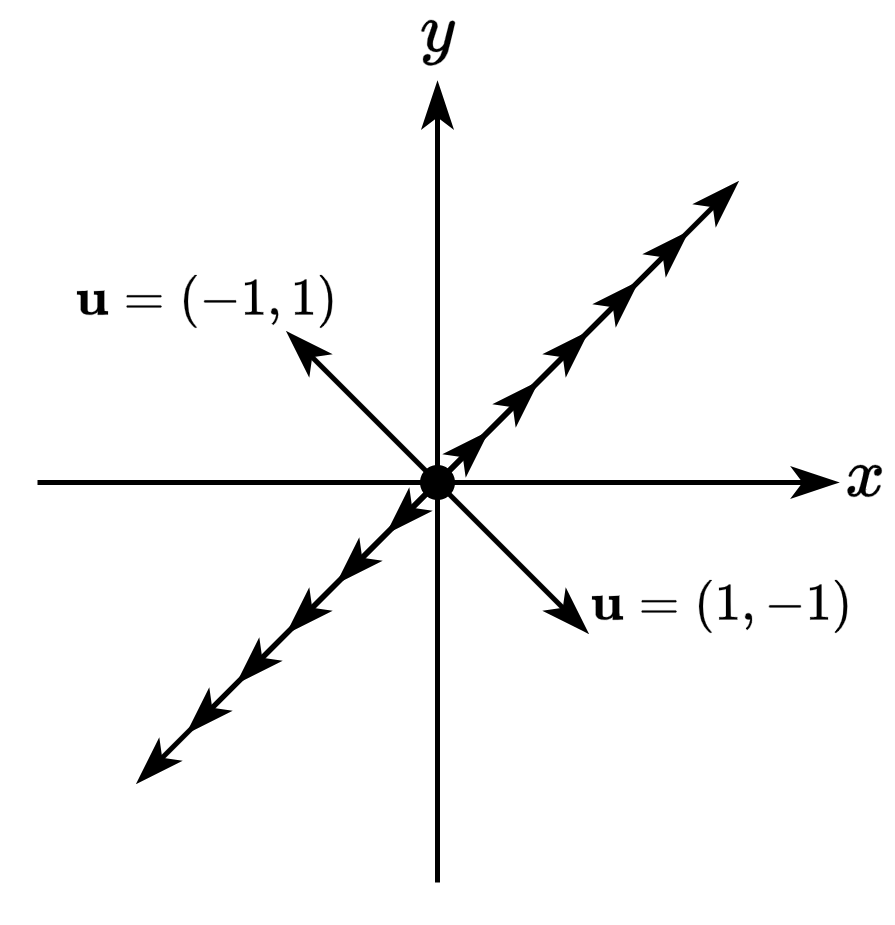
  \[\begin{bmatrix} 1 & -1\\ -1 & 1 \end{bmatrix}\]
  • 위 선형 변환해 의해 원점에서 \(y=x\) 위의 점을 가리키는 벡터가 모두 \((0, 0)\)이 됨
  • 여기서 \(y=x\) 위의 점을 가리키는 모든 벡터, 즉, 영벡터가 되는 모든 벡터들의 집합을 영공간이라고 함
• 공간이 축소되는 경우에만 공집합이 아님
• \(n\)차원에서 \(n-a\)차원으로 축소되는 경우 영공간의 차원은 \(a\)
  • 예)
    • 2차원에서 1차원(직선)으로 축소되는 경우 영공간의 차원은 1차원
    • 3차원에서 1차원(직선)으로 축소되는 경우 영공간의 차원은 2차원(평면)

nullity

• 영공간의 차원을 \(\text{nullity}(\mathbf{A})\)와 같이 표기

• 예)

  

  \[\begin{bmatrix} 1 & -1\\ -1 & 1 \end{bmatrix}\]
  • 2차원을 1차원으로 축소시키는 변환 행렬
  • $\text{nullity}(\mathbf{T})=1$

랭크와 nullity의 관계

• $\text{rank}(\mathbf{A}_n) + \text{nullity}(\mathbf{A}_n) = n$
• \(n\)차원 공간을 변형하는 변환 행렬의 랭크와 nullity를 더하면 반드시 \(n\)
  • 랭크는 변환된 공간의 차원, nullity는 축소되어 영벡터가 된 벡터 집합의 차원
  • 따라서 둘이 더하면 반드시 변환 전 공간의 차원일 수 밖에 없음