선형대수학 for Graphics Chapter 6. 벡터의 내적과 외적

내적(inner product)

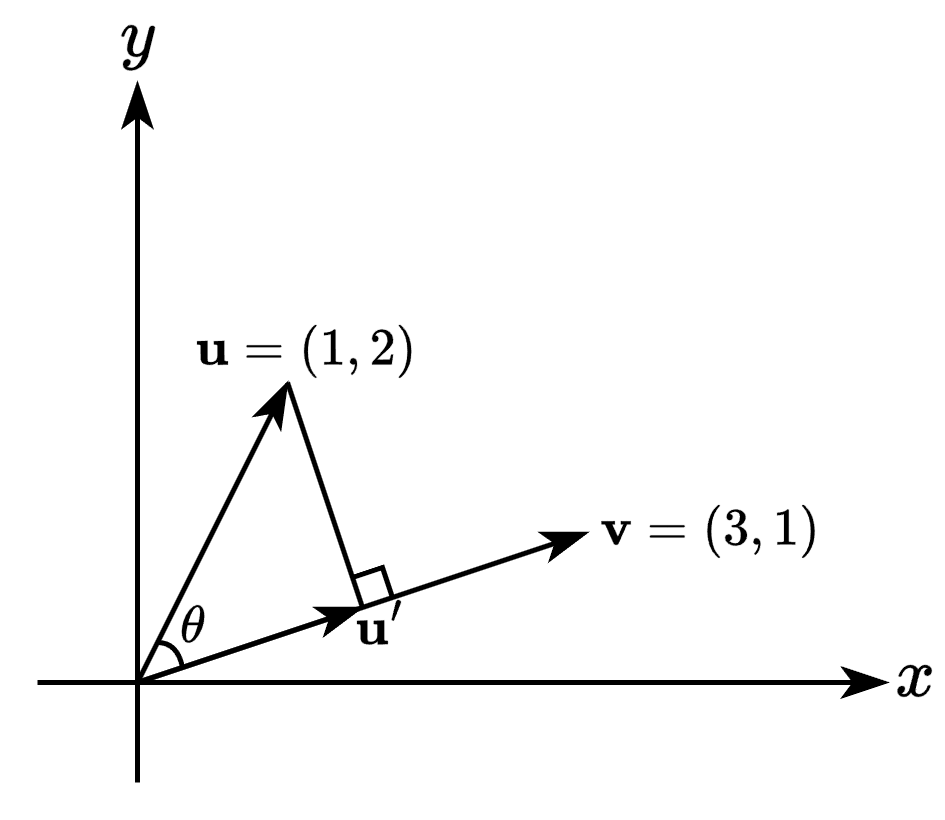
\[\mathbf{u} \cdot \mathbf{v} =\left\Vert\mathbf{u}\right\Vert\cos{\theta} \left\Vert\mathbf{v}\right\Vert =\left\Vert\mathbf{u}\right\Vert \left\Vert\mathbf{v}\right\Vert\cos{\theta} =\mathbf{v} \cdot \mathbf{u}\]

• 내적: 벡터(\(\mathbf{u}\))에서 다른 벡터(\(\mathbf{v}\))로 투영한 벡터(\(\mathbf{u}^\prime\))의 길이(\(\left\Vert\mathbf{u}^\prime\right\Vert\))와 다른 벡터의 길이(\(\left\Vert\mathbf{v}\right\Vert\))를 곱하는 연산
• 점(\(\cdot\)) 연산자 사용
• 계산 순서가 바뀌어도 결과는 같음

내적과 선형 변환

• 벡터를 다른 벡터에 투영한 벡터의 길이를 선형 변환을 이용해 구할 수 있음
  • 벡터를 넣어 스칼라 값(1차원 벡터)이 나오는 선형 변환

• \(\mathbf{u}\)를 \(\mathbf{v}\)에 투영하는 것을 \(\mathbf{u}\)가 포함된 표준 공간을 \(\mathbf{v}\)​방향의 직선 공간으로 압축하는 것으로 생각할 수 있음
  • 여기서 \(\mathbf{v}\)방향의 직선 공간을 1차원 공간으로 생각하면 \(\mathbf{u}^\prime\)​의 길이를 간단하게 구할 수 있음

\(\mathbf{v}\)가 단위 벡터인 경우

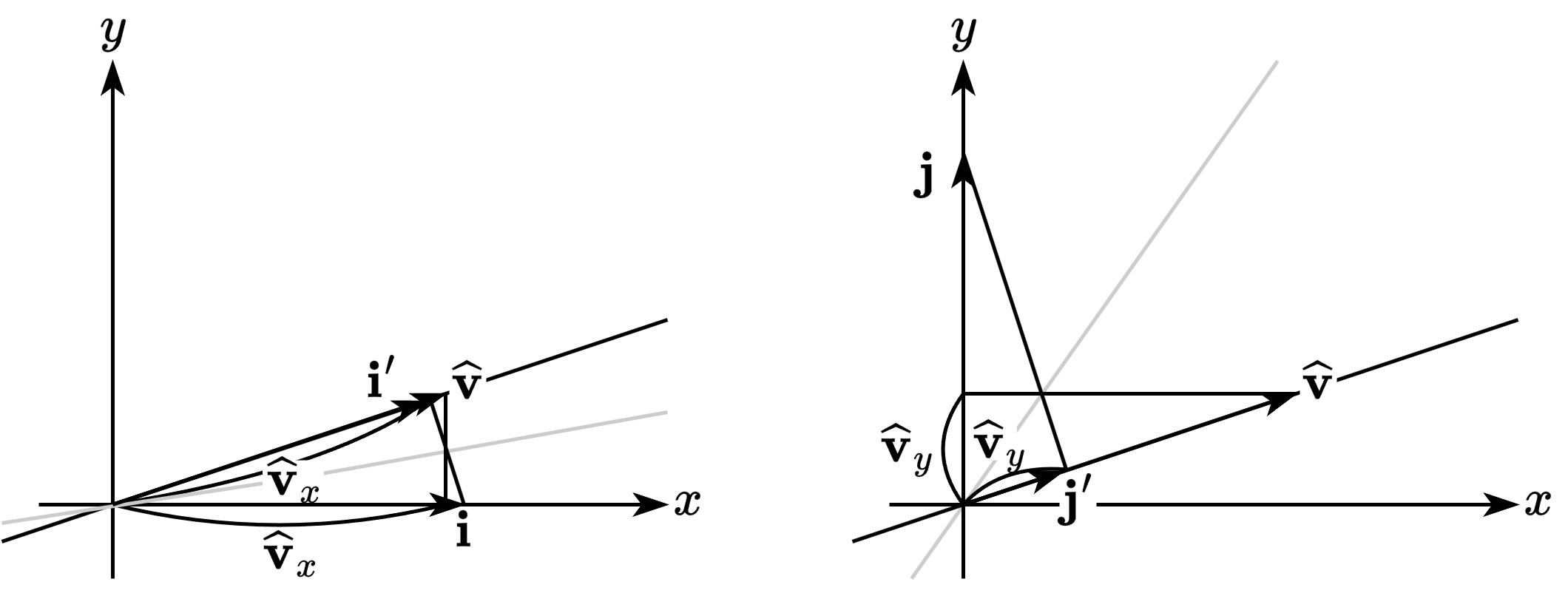
• 표준 기저 벡터를 \(\mathbf{v}\)​방향의 직선 공간에 투영한 벡터의 길이를 구하는 과정
  • 표준 기저 벡터의 투영된 벡터를 2차원으로 표현하는 대신 1차원(\(\mathbf{v}\)​방향의 직선)으로 생각
  • 따라서 새로운 기저 \(\mathbf{i}^\prime = \hat{\mathbf{v}}_x\), \(\mathbf{j}^\prime = \hat{\mathbf{v}}_y\)​를 계산

참고로 위와 같이 어떤 구조를 뒤집어서 생각하는 것을 duality라고 함 (\(\hat{\mathbf{v}}\) 방향의 직선 공간으로 투영한 기저를 구할 때, 역으로 \(\hat{\mathbf{v}}\)를 기저에 투영하여 대칭을 이용함)

• \(\mathbf{u}=(x, y)\)를 \(\hat{\mathbf{v}}\)에 투영하면 \(\mathbf{u}^\prime=x\mathbf{i}^\prime + y\mathbf{j}^\prime\)
  • 선형 변환은 기저 벡터들에 의해 결정되기 때문에 이러한 계산이 성립

  • \(\mathbf{u}^\prime\)는 1차원 벡터이므로 \(\hat{\mathbf{v}}\)에 투영된 \(\mathbf{u}\)​​의 길이와 같음

    \[\hat{\mathbf{v}}\cdot\mathbf{u}=x\hat{\mathbf{v}}_x+y\hat{\mathbf{v}}_y\]
    • 투영된 길이에 \(\hat{\mathbf{v}}\)의 길이를 곱해야 하지만 단위 행렬(길이가 1)이므로 생략

\(\mathbf{v}\)가 단위 벡터가 아닌 경우

• \(\mathbf{v}\)가 단위 벡터가 아닌 경우에는 단위 벡터인 경우의 계산법(\(\hat{\mathbf{v}}\cdot\mathbf{u}=x\hat{\mathbf{v}}_x+y\hat{\mathbf{v}}_y\))에 \(\mathbf{v}\)의 길이를 곱해주면 됨

• \(\mathbf{v}\)의 길이를 \(n\)이라 하면

  \[\begin{align*} \mathbf{v}\cdot\mathbf{u} &=(x\hat{\mathbf{v}}_x+y\hat{\mathbf{v}}_y)n\\ &=x\hat{\mathbf{v}}_xn+y\hat{\mathbf{v}}_yn\\ &=x(\hat{\mathbf{v}}_xn)+y(\hat{\mathbf{v}}_yn)\\ &=x\mathbf{v}_x+y\mathbf{v}_y \end{align*}\]
  • 삼각형에서 빗면의 길이가 \(n\)​배 늘어나면 밑면과 높이의 길이도 \(n\)​배 늘어나므로 위와 같이 표현 가능

\[\mathbf{u}\cdot\mathbf{v}=\left\Vert\mathbf{u}\right\Vert \left\Vert\mathbf{v}\right\Vert\cos{\theta}=\mathbf{u}_x\mathbf{v}_x+\mathbf{u}_y\mathbf{v}_y=[\mathbf{u}_x\;\mathbf{u}_y]\begin{bmatrix}\mathbf{u}_x\\\mathbf{u}_y\end{bmatrix}\]

내적의 성질

• 두 벡터가 이루는 각에 따라 부호가 달라짐
  • \(\lt 90^\circ\): 양수(\(+\)​)
  • \(= 90^\circ\): 0
  • \(\gt 90^\circ\): 음수(\(-\))

외적(cross product)

• \(\mathbf{u} \times \mathbf{v}=\mathbf{n}\): \(\mathbf{u}\)와 \(\mathbf{v}\)를 외적
• 크로스 연산자(\(\times\)​)를 사용
• 외적의 결과는 벡터

외적과 평행사변형

• \(\left\Vert\mathbf{u} \times \mathbf{v}\right\Vert=\left\Vert\mathbf{u}\right\Vert \left\Vert\mathbf{v}\right\Vert\sin{\theta}\): 외적의 결과 벡터의 길이는 \(\sin\)​을 이용해 계산 가능
  • \(\theta\)는 \(\mathbf{u}\)에서 \(\mathbf{v}\)로의 반시계 방향 각
• 외적의 절대값
  • 두 벡터가 이루는 평행사변형의 넓이를 의미
• 부호
  • 두 벡터가 이루는 각(작은 각)을 기준으로
  • \(\mathbf{v}\)가 \(\mathbf{u}\)보다 반시계 방향에 있으면 \(+\)
  • \(\mathbf{v}\)가 \(\mathbf{u}\)보다 시계 방향에 있으면 \(-\)
• 따라서 외적은 곱하는 순서가 변함에 따라 부호가 바뀜

외적과 행렬식(2차원)

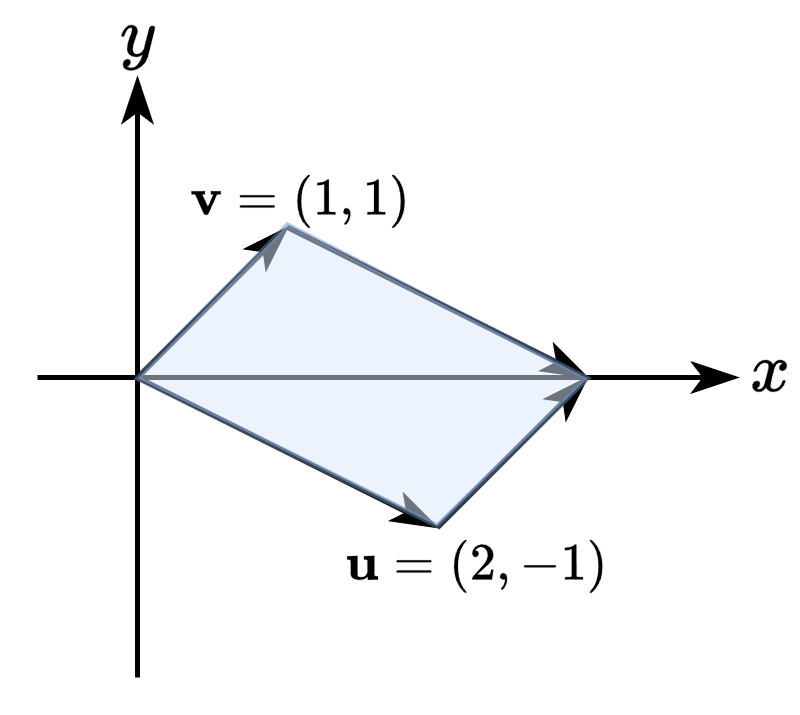
• \(\mathbf{i}\)가 \(\mathbf{u}\)로, \(\mathbf{j}\)가 \(\mathbf{v}\)로 기저 변환 되었다고 생각하면 행렬식을 통해 평행사변형의 넓이 계산 가능

  \[\begin{vmatrix} 2 & -1\\ 1 & 1 \end{vmatrix}=3\]

외적과 행렬식(3차원)

\[\begin{bmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ u_x & u_y & u_z\\ v_x & v_y & v_z\\ \end{bmatrix} =\mathbf{i}\det\begin{bmatrix}u_y & u_z\\ v_y & v_z\\\end{bmatrix} + \mathbf{j}\det\begin{bmatrix}u_z & u_x\\ v_z & v_x\\\end{bmatrix} + \mathbf{k}\det\begin{bmatrix}u_x & u_y\\ v_x & v_y\\\end{bmatrix}\]

외적이 만드는 벡터의 의미

• 내적과 다르게 외적의 결과는 벡터

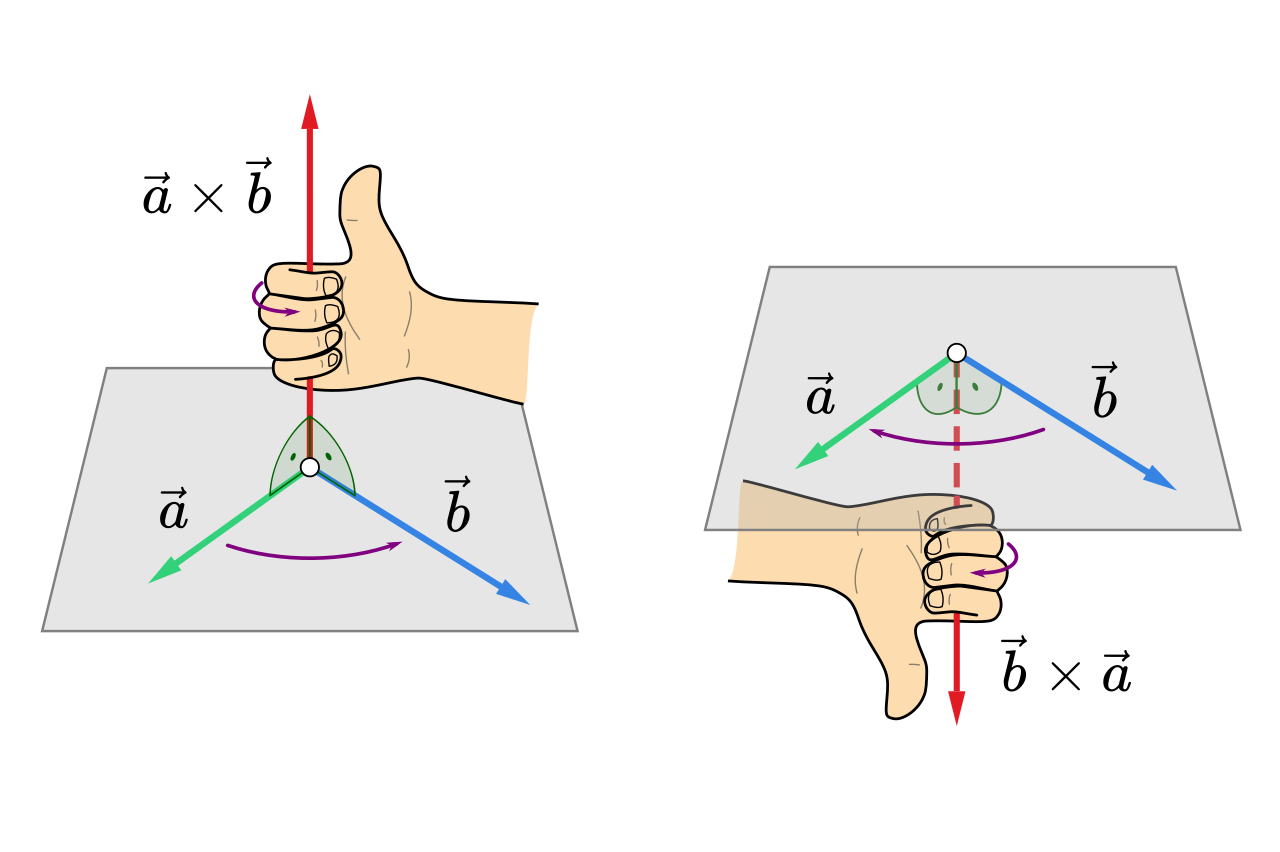By MikeRun - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=116897682

• 외적은 두 벡터와 수직인 벡터를 계산
  • 위 그림처럼 오른손의 법칙을 이용해 어느 방향으로 수직인지 알 수 있음

증명

• 외적을 계산할 벡터 \(\mathbf{u}=(u_x, u_y, u_z)\), \(\mathbf{v}=(v_x, v_y, v_z)\)와 임의의 벡터 \(\mathbf{a} = (x, y, z)\)로 구성된 행렬 \(\mathbf{M}\)에 대하여

  \[\mathbf{M}=\begin{bmatrix} x & y & z\\ u_x & u_y & u_z\\ v_x & v_y & v_z \end{bmatrix}\]
  • \(\det{\mathbf{M}}\)는 \(\mathbf{u}\), \(\mathbf{v}\), \(\mathbf{a}\)가 이루는 평행육면체(parallelepiped)의 부피의 절대값을 의미
  \[\begin{align*} \det{\mathbf{M}}= \mathbf{p}\cdot\mathbf{a} = \begin{bmatrix} p_x & p_y & p_z \end{bmatrix} \cdot \begin{bmatrix} x & y & z \end{bmatrix} &= \begin{vmatrix} x & y & z\\ u_x & u_y & u_z\\ v_x & v_y & v_z \end{vmatrix}\\ &=x(u_yv_z-u_zv_y)-y(u_zv_x-u_xv_z)+z(u_xv_y-u_yv_x)\\ &=p_xx+p_yy+p_zz \end{align*}\] \[\begin{align*} \therefore \; &p_x=u_yv_z-u_zv_y\\ &p_y=u_xv_z-u_zv_x\\ &p_z=u_xv_y-u_yv_x \end{align*}\]
  • 또한 평행육면체의 부피는 밑면(\(\mathbf{u}\)와 \(\mathbf{v}\)가 이루는 평행사변형)과 높이(\(\mathbf{a}\)를 \(\mathbf{u}\)와 \(\mathbf{v}\)에 모두 수직인 직선에 투영한 벡터의 길이)의 곱
    • 이것은 (\(\mathbf{a}\))와 (\(\mathbf{u}\), \(\mathbf{v}\)와 수직이며 \(\mathbf{u}\), \(\mathbf{v}\)가 이루는 평행사변형의 넓이를 길이로 가지는 벡터 \(\mathbf{w}\))의 내적으로 나타낼 수 있음
    • 내적은 (벡터를 다른 벡터에 투영시킨 벡터의 길이) * (다른 벡터의 길이)
    • \(\mathbf{a}\)를 \(\mathbf{w}\)에 투영시킨 벡터의 길이는 평행육면체의 높이, \(\mathbf{w}\)의 길이는 \(\mathbf{u}\), \(\mathbf{v}\)가 이루는 평행사변형의 넓이
    • 따라서 \(\mathbf{a} \cdot \mathbf{w}\)는 높이와 밑면의 곱, 즉 평행육면체의 부피
  • 두 식을 합치면 \(\mathbf{p} \cdot \mathbf{a} = \mathbf{a} \cdot \mathbf{w}\), \(\mathbf{p}=\mathbf{w}\)
  • 따라서 \(\mathbf{u} \times \mathbf{v} = [u_yv_z-u_zv_y, u_xv_z-u_zv_x, u_xv_y-u_yv_x]\)는 두 벡터와 수직이며 길이는 두 벡터가 이루는 평행사변형의 넓이인 벡터