머신러닝 1. 머신러닝의 기초

1. 머신러닝이란?

• 컴퓨터가 데이터를 통해 학습하고 개선해 나가는 방법
• 지도 학습, 비지도 학습, 강화 학습으로 나뉨
  • 지도 학습(supervised learning)
    • 정답이 있는 데이터를 통해 학습
    • 회귀, 분류 등이 해당
  • 비지도 학습(unsupervised learning)
    • 정답이 없는 데이터를 통해 학습
    • 군집화, 생성 알고리즘 등이 해당
  • 강화 학습(reinforcement learning)
    • 보상을 최대화 하기 위해 시행착오를 거쳐 학습

2. 기본 용어

• 데이터(data): 관찰이나 실험, 조사등을 통해 얻은 자료(문자, 숫자, 소리 등)
  • 데이터셋(data set, \(D = \{\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_m\}\)): 데이터들의 집합
  • 사례(instance, \(\mathbf{x}_i = (\mathbf{x}_{i1}; \mathbf{x}_{i2}; ...; \mathbf{x}_{id})\)) 또는 샘플(sample): 데이터셋에서 속한 하나의 데이터
  • 속성(attribute) 또는 특성(feature): 데이터의 특정 성질
    • 예) 자동차의 색, 크기, 바퀴 모양 등
    • 속성값(attribute value, \(\mathbf{x}_{ij}\)): 속성에 관한 값
    • 속성 공간(attribute space): 속성값들의 집합
  • 샘플 공간(sample space, \(\mathcal{X}\)): 다양한 샘플들의 집합, 속성 공간의 확장
    • 차원수(dimensionality): 샘플 공간 \(\mathcal{X}\)위 하나의 벡터 \(\mathbf{x}_i \in \mathcal{X}\)​의 속성의 개수
    • \(\vert \mathcal{X} \vert\): 샘플 공간 \(\mathcal{X}\)에 속한 샘플의 개수, \(\mathcal{X}\)의 크기
• 레이블(label, \(y_i\)): 결과를 나타내는 정보, \((\mathbf{x}_i, y_i)\)는 \(i\)번째 샘플의 레이블을 의미
  • 레이블 공간(label space, \(\mathcal{Y}\)): 레이블들의 집합, \(y_i \in \mathcal{Y}\)
• 학습(learning) 또는 훈련(training): 데이터를 통해 모델(model)을 만드는 과정
  • \(\mathcal{X}\)를 \(\mathcal{Y}\)에 투영하는 식을 찾는 과정, \(\mathcal{X} \mapsto \mathcal{Y}\)
  • 훈련 데이터(training data): 훈련에 사용되는 데이터
  • 훈련 세트(traning set): 훈련 데이터셋
  • 훈련 샘플(training sample): 훈련 데이터셋의 샘플
• 검증(testing): 학습이 완료된 최종 모델이 정상적으로 작동하는지 확인하는 과정
  • 테스트 샘플(testing sample): 검증을 위해 사용되는 샘플
• 가설(hypothesis): 학습 모델이 예측(prediction)한 데이터 속 규칙
  • 학습은 가설이 진실(ground-truth)을 예측하기 위한 과정
    • 훈련셋 \(\{(\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), ..., (\mathbf{x}_m, y_m)\}\)을 바탕으로 학습하여 \(\mathcal{X}\)에서 \(\mathcal{Y}\)를 예측하는 가설 \(h(\mathbf{x})\)를 찾는 것
• 분류(classification): 예측하려는 값이 이산적인 문제
  • 예) 나이(년), 소유하고 있는 자동차 수
  • 이진 분류(binary classification): 예측하려는 값이 두 가지 종류인 경우
    • 예) 종양의 양성, 음성 여부
• 회귀(regression): 예측하려는 값이 연속적인 문제
  • 예) 키, 몸무게
• 군집화(clustering): 데이터에 내재된 패턴에 따라 군집(cluster)으로 나누는 문제
  • 레이블이 없는 비지도 학습
  • 예) 기사 카테고리, 영화 테마
• 일반화(generalization): 훈련 세트 외의 데이터에서도 잘 작동하는 것
  • 샘플 공간을 잘 나타낼 수록 일반화된 모델이라 함
  • 샘플 공간의 모든 샘플이 미지의 분포 \(\mathcal{D}\)를 보인다고 가정
    • 독립항등분포(independent and identicaly distributed, i.i.d.): 모든 샘플들은 서로 독립적으로 \(\mathcal{D}\)에서 채집
    • 따라서 샘플이 많을수록 \(\mathcal{D}\)에 대해 잘 알 수 있고, 학습을 통해 얻는 모델의 일반성을 강화

3. 가설 공간

• 귀납 학습(inductive learning): 샘플을 통해 학습하는 과정
  • 넓은 의미: 샘플을 통해 배우는 것
  • 좁은 의미: 훈련 데이터에서 개념(concept)을 배우는 것
    • 따라서 개념 학습이라고 부름
    • 부울(Boolean) 개념 학습: True나 False와 같은 불리언 값을 가진 목표 개념을 학습
• 학습을 여러 가설로 이루어진 가설 공간에서 훈련 데이터와 가장 잘 맞는(fit) 가설을 찾는 과정이라 할 수 있음
  • 현실에서는 매우 큰 가설 공간을 만나게 됨
  • 하지만 훈련 데이터는 한정적
  • 따라서 많은 가설이 훈련 데이터와 잘 맞을 수 있음
    • 이러한 가설들의 집합을 버전 공간(version space)이라고 함

4. 귀납적 편향

• 훈련 데이터와 잘 맞는 가설이 여러개 있을 수 있음
  • 이러한 가설들은 훈련 데이터에 없는 데이터에 대해 다른 결과를 내놓을 수도 있음
  • 따라서 어떤 가설을 최종적으로 선택할지는 매우 중요한 문제
• 머신러닝 알고리즘이 학습할 때는 항상 특정한 유형의 가설에 대한 귀납적 편향(inductive bias)를 가지고 있음
  • 일반적인 모델을 좋아한다면 일반적인 가설에 대해 기울어진 편향
  • 특수한 모델을 좋아한다면 특수한 가설에 대해 기울어진 편향
  • 만약 편향을 가지고 있지 않다면?
    • 어떤 가설을 선택할지 모르기 때문에 혼란에 빠질 수 있음

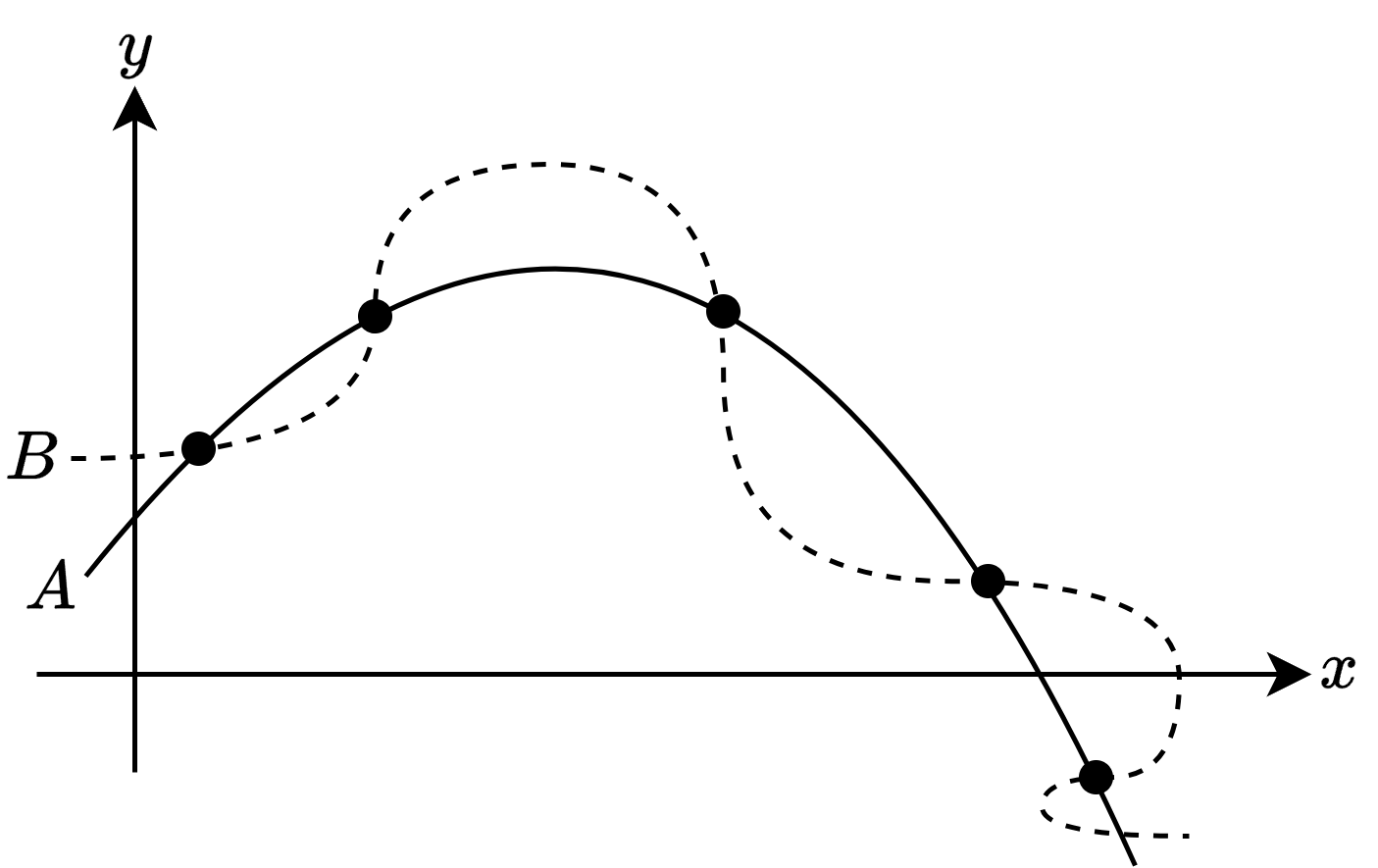
오컴의 면도날(Occam’s razor)

• 다수의 가설에서 관측된 결과가 일치하다면, 가장 간단한 것을 선택해야 한다는 원칙

• 만약 ‘평활함’이 간단함을 의미한다면 위 두 가설(\(A\), \(B\)) 중 \(A\)를 선택하는 것이 현명
  • 따라서 \(A\)에 대한 편향을 갖게 됨
• 하지만 실제로는 오른쪽 그림처럼 다른 경우가 존재할 수 있음
  • 또한 현재의 가설이 간단한지 평가하는 것도 쉽지 않음

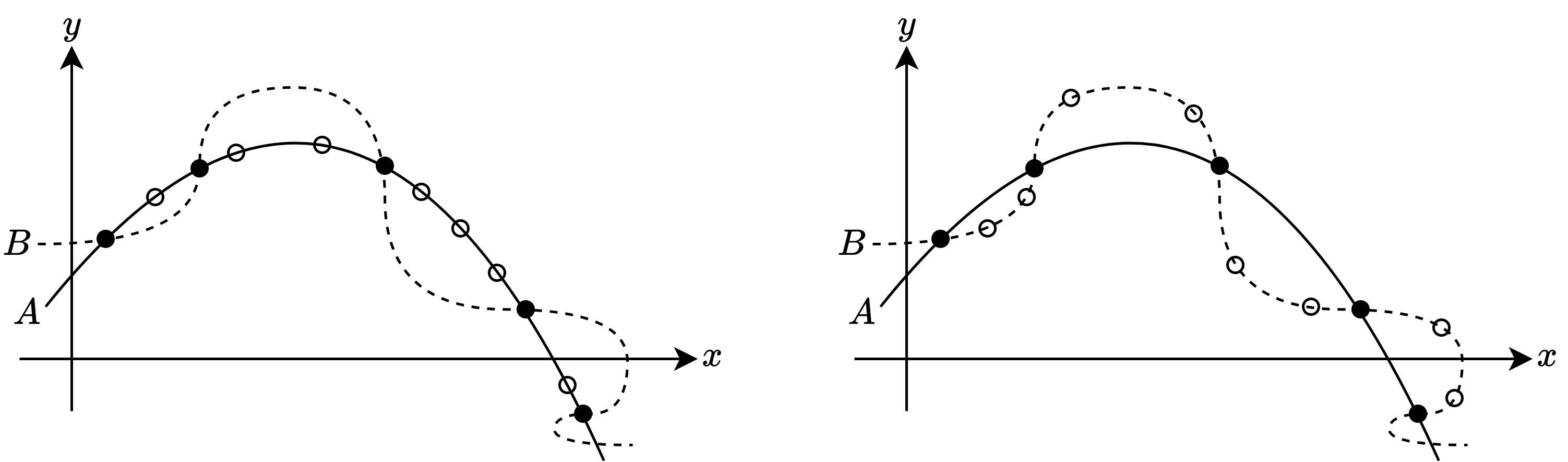
• 학습 알고리즘 \(\mathfrak{L}_a\)는 어떠한 편향에 의해 \(A\)를 선택했고, 다른 학습 알고리즘 \(\mathfrak{L}_b\)는 \(B\)를 선택했다고 가정
  • ‘평활함’이 단순함이라면 \(\mathfrak{L}_a\)는 \(\mathfrak{L}_b\)보다 좋은 알고리즘이라 할 수 있음
    • 왼쪽 그림처럼 테스트 데이터에 대해서도 잘 일치함
  • 하지만 오른쪽 그림과 같은 경우가 나올 수도 있음
    • 테스트 데이터가 오히려 \(A\)보다 \(B\)에 더 일치함
  • 이처럼 어떤 문제에 대해서는 \(\mathfrak{L}_a\)가 더 좋은 성능을 내지만, 다른 문제에 대해서는 \(\mathfrak{L}_b\)​가 더 좋은 성능을 낼 수도 있음

공짜 점심은 없다(No Free Lunch Theorem, NFL)

• 알고리즘이 얼마나 똑똑하든, 멍청하든 상관 없이 기대 성능은 언제나 같다.
• 전제
  • 모든 문제가 출현하는 기회가 같음
  • 모든 문제가 똑같이 중요

\[E_{ote}(\mathfrak{L}_a \mid X, f) = \sum_h \sum_{\mathbf{x} \in \mathcal{X} - X} P(\mathbf{x}) \mathbb{I}(h(x) \neq f(x)) P(h \mid X, \mathfrak{L}_a)\]

• 훈련 데이터 외의 데이터에게 갖는 오차를 나타내는 식
  • \(P(h \mid X, \mathfrak{L}_a)\): 훈련 데이터 \(X\)에 기반해 알고리즘 \(\mathfrak{L}_a\)가 생성한 가설이 \(h\)일 확률
  • \(f\): 학습하고자 하는 목표 함수
  • \(\mathbb{I}()\): 지시 함수(indicator function), 괄호 안 내용이 진실이면 \(1\), 거짓이면 \(0\)을 가짐
• 이진 분류 문제에서 만약 목표 함수가 모든 함수 \(\mathcal{X} \mapsto \{0, 1 \}\)이 될 수 있다면, 함수 공간은 \(\{0, 1 \}^{\vert \mathcal{X} \vert}\)

\[\begin{align*} \sum_f E_{ote}(\mathfrak{L}_a \mid X, f) &= \sum_f \sum_h \sum_{\mathbf{x} \in \mathcal{X} - X} P(\mathbf{x}) \mathbb{I}(h(x) \neq f(x)) P(h \mid X, \mathfrak{L}_a)\\ &= \sum_{\mathbf{x} \in \mathcal{X} - X} P(\mathbf{x}) \sum_h P(h \mid X, \mathfrak{L}_a) \sum_f \mathbb{I}(h(x) \neq f(x))\\ &= \sum_{\mathbf{x} \in \mathcal{X} - X} P(\mathbf{x}) \sum_h P(h \mid X, \mathfrak{L}_a) \frac{1}{2}2^{\vert \mathcal{X} \vert}\\ &= \frac{1}{2}2^{\vert \mathcal{X} \vert} \sum_{\mathbf{x} \in \mathcal{X} - X} P(\mathbf{x}) \sum_h P(h \mid X, \mathfrak{L}_a)\\ & = 2^{\vert \mathcal{X} \vert - 1} \sum_{\mathbf{x} \in \mathcal{X} - X} P(\mathbf{x}) \cdot 1\\ \end{align*}\]

• 모든 가능한 \(f\)에 대한 오차의 합

  • 위 식에 따르면 총오차는 학습 알고리즘과 무관

    \[\sum_f E_{ote} (\mathfrak{L}_a \mid X, f) = \sum_f E_{ote} (\mathfrak{L}_b \mid X, f)\]
  • 학습 알고리즘 \(\mathfrak{L}_a\)가 얼마나 똑똑하든, \(\mathfrak{L}_b\)가 얼마나 멍청하는 상관 없이 기대 성능은 언제가 같음
  • 이 정리를 공짜 점심은 없다 정리(No Free Lunch Theorem, NFL)라고 함

• 따라서 문제에 상관없이 어떤 학습 알고리즘이 좋은가 고민하는 것은 아무런 의미가 없음

  • 반드시 어떤 문제를 해결할 것인지 생각하고 알고리즘을 평가해야 함
  • 예)
    • 서울에서 부산까지 가는 문제에서는 KTX, 비행기 등 좋은 알고리즘이 많음
    • 하지만 서울에서 춘천까지 가는 문제에서 KTX나 비행기가 좋지 않다고 해서 신경 쓸 필요는 없음
      • 춘천에는 KTX 노선이 없으며 공항도 없음
    • 따라서 어떤 문제(서울-부산, 서울-춘천)인지 생각하기 전에 KTX나 비행기를 이용하는 것이 좋은지 평가하는 것은 의미가 없음
  • 어떤 문제에서 매우 좋은 성능을 보인 알고리즘이 다른 문제에서 나쁜 성능을 보이는 것은 학습 알고리즘의 편향과 문제가 잘 맞지 않음을 의미

5. 발전 과정

• 논리 이론가 프로그램, 일반 문제 해결 프로그램
  • 수학 정리 증명
• 연결주의 학습: 퍼셉트론, 에디아라인(Adaline) 등
  • 역전파 알고리즘으로 인해 큰 주목
  • 딥러닝의 등장
• 기호주의 학습: 의사결정 트리 등
• 통계 학습: SVM, 커널 기법, VC 차원