머신러닝 2. 모델 평가 및 선택

1. 경험 오차 및 과적합

• 오차율(error rate): 전체 샘플(\(m\)개)에서 잘못 분류한 샘플(\(a\)개)의 비율, \(E = a / m\)​
• 정확도(accuracy): 1 - 오차율, \(1 - a / m\)
• 오차(error): 예측 값과 실제 값 사이의 차이
  • 훈련 오차(training error) 또는 경험 오차(empirical error): 훈련 세트에서 발생한 오차
  • 일반화 오차(generalization error): 새로운 샘플에서 발생한 오차
    • 우리의 목표는 일반화 오차를 줄이는 것
    • 하지만 사전에 새로운 샘플에 대한 정보를 얻을 수 없기 때문에 일반화 오차를 구하는 것을 불가능
    • 따라서 일반화 오차 대신 경험 오차를 줄이는 것을 목표로 학습
• 과적합(overfitting): 모델이 훈련 데이터에 지나치게 학습된 상태
  • 경험 오차는 거의 0에 수렴
  • 일반화 오차는 매우 큼
  • 훈련 데이터의 일반적인 특징만 찾아야 하는데, 별로 중요하지 않은 특징까지 학습한 결과
  • 모델 훈련에서 넘어야 할 큰 장애물
• 과소적합(underfitting): 모델이 훈련 데이터에 특징을 잘 찾지 못한 상태
  • 경험 오차와 일반화 오차 모두 매우 큼
  • 학습을 더 진행하거나 트리의 가지를 늘리는 방법으로 해결 가능

2. 테스트 방법

• 테스트 세트(testing set): 학습 과정에서 만나보지 못했던 새로운 샘플의 집합
  • 테스트 오차(testing error): 테스트 세트에서의 오차
    • 일반화 오차의 근삿값으로 생각
  • 테스트 오차의 정확한 계산을 위해 테스트 세트는 훈련 세트와 겹치는 샘플이 있어서는 안됨

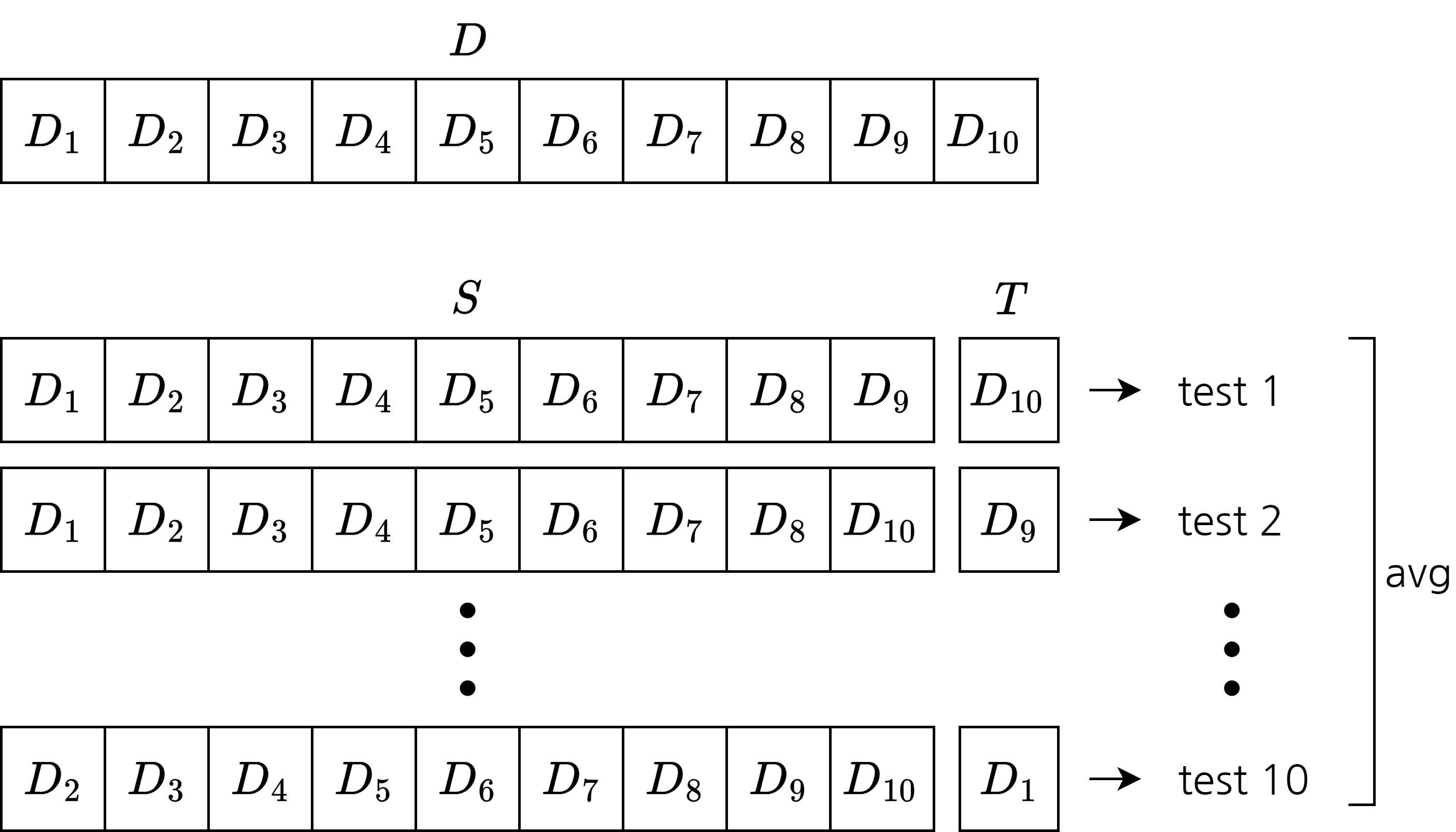
데이터셋(\(D\))을 훈련 세트(\(S\))와 테스트 세트(\(T\))로 나누는 방법

홀드아웃(hold-out)

• 홀드아웃 방법 또는 검증 세트 기법: \(D\)를 겹치지 않는 임의의 두 집합 \(S\)와 \(T\)로 분할
  • \(D = S \cup T\), \(S \cap T = \varnothing\)
  • 예)
    • \(D\)에 1,000개의 샘플이 있을 때 \(S\)에 700개, \(T\)에 300의 샘플로 분할
    • 만약 모델이 \(T\)에서 90개의 샘플을 잘못 분류했다면
      • 오차율은 \(E = 90 / 300 = 30\%\)
      • 정확도는 \(1 - 30\% = 70\%\)
• 층화 추출법(stratified sampling): 샘플의 데이터 분포를 같게 나누는 방법
  • 예) 이진 분류
    • 양성 데이터와 음성 데이터가 각각 500개
    • \(S\)의 비율이 \(70\%\), \(T\)의 비율이 \(30\%\)
    • 양성, 음성 데이터가 \(S\)에는 350개씩, \(T\)에는 150개씩 들어 있음
• 다른 방법으로는 랜덤으로 \(n\)번 분류 후 평균을 계산해 분류할 수도 있음
  • 예) 이진 분류
    • 랜덤하게 100번 분할했을 때의 \(S\), \(T\)의 양성, 음성 데이터 개수의 평균을 계산해 최종 분할
• \(S\)와 \(T\)의 비율을 정하는 것도 매우 중요
  • \(S\)의 개수가 많을 수록 모델은 \(D\)에 가깝게 학습되지만, 테스트 결과는 불안정적
    • 분산이 크고 편향이 작음
  • \(T\)의 개수가 많을수록 \(S\)와 \(D\)의 차이가 벌어지기 때문에 모델이 편향될 수 있음
    • 편향이 크고 분산이 작음
  • 따라서 대부분 20~30%를 테스트 세트로 사용

교차 검증(cross validation)

• k-폴드 교차 검증(k-fold cross validation)

  

  • \(D\)를 \(k\)개의 서로소 집합으로 분할
    • \(D = D_1 \cup D_2 \cup \cdots \cup D_k\), \(D_i \cap D_j = \varnothing\)
    • 각 부분집합이 데이터 분포를 잘 반영하도록 층화 추출법을 이용해 분할
  • 아래 방법으로 \(k\)번 학습, 테스트
    • \(D_i\)를 \(T\)로, 나머지를 \(S\)로 사용
  • \(k\)에 따라 테스트 결과의 안정성이 달라짐
    • \(k\)는 주로 10, 5, 20을 사용
  • 이러한 과정을 \(p\)번 랜덤한 부분집합을 이용해 반복
    • 즉, 최종 결과는 \(p\)번의 k-fold를 실행한 값을 평균
    • 주로 10차 10-fold 교차 검증을 사용(즉 100번의 테스트를 진행)

• LOOCV(Leave-One-Out Cross Validation): \(m\)개의 샘플이 있는 \(D\)에 대하여 \(k=m\)인 k-fold를 실행

  • \(S\)가 \(D\)와 비교했을 때 1개의 샘플만 차이나기 때문에 학습된 모델이 \(D\)와 매우 비슷
    • 편향이 작음
  • 하지만 \(m\)이 클 때, 계산량이 많다는 단점이 있음

부트스트래핑(bootstrapping)

• 부트스트랩 샘플링(bootstrap sampling)이라고도 함

• \(m\)개의 샘플이 있는 \(D\)에서 랜덤한 샘플을 \(m\)번 복사해 \(D^\prime\)을 생성

  • 샘플을 가져오는 것이 아닌 복사해오는 것

  • \(D^\prime\)에 중복된 데이터가 있을 수 있음

  • \(D\)에서 한 번도 선택되지 않은 데이터가 있을 수 있음

    • \(m\)번의 샘플링 과정에서 한 번도 뽑히지 않을 확률: \((1 - 1/m)^m\) \(\lim_{m \rightarrow \infty}\left(1 - \frac{1}{m} \right)^m=\frac{1}{e} \approx 0.368\)

    • 따라서 \(D\)의 36.8%의 샘플은 \(D^\prime\)에 포함되지 않음

• \(D^\prime\)은 훈련 세트로, \(D - D^\prime\)은 테스트 세트로 사용

  • 운이 좋으면 \(m\)개의 데이터를 모두 훈련에 활용할 수 있음
  • 활용하지 못한 데이터가 있더라고 테스트에 사용할 수 있음
  • 이러한 테스트를 Out-of-Bag라고 함

• 부트스트래핑은 주로 데이터셋이 적거나 훈련, 테스트 세트로 분류하기 어려울 때 사용

  • 또한 초기 데이터셋에서 다양한 훈련 세트를 만들 수 있기에 앙상블 기법에 적용하기 좋음

파라미터 튜닝

• 파라미터(parameter): 학습 과정에서 조율(tuning)해야 하는 값
  • 파라미터를 어떻게 설정하는가에 따라 모델의 성능이 크게 차이남
  • 하이퍼 파라미터(hyper parameter): 학습 알고리즘에서 설정해야 하는 파라미터
    • 주로 10개 이하
    • 사람이 직접 설정
  • 모델 파라미터(model parameter): 모델의 파라미터
    • 많은 경우 1억개 이상
    • 학습하며 업데이트
• 모델을 선택하는 것 만큼 파라미터를 설정하는 것도 중요
• 검증 세트(validation set): 모델 평가 및 선택 과정에서 아용되는 데이터
  • 테스트 세트는 최종 모델의 성능을 측정할 때 사용
  • 검증 세트는 모델의 파라미터 튜닝이나 모델 선택에 사용

3. 모델 성능 측정

• 성능 측정(performance measure): 모델의 일반화 성능을 평가할 기준
  • 서로 다른 모델의 성능을 비교할 때 일관된 성능 측도가 필요

평균 제곱 오차(mean squared error)

\[E(f;D)=\frac{1}{m}\sum_{i=1}^m(f(\mathbf{x}_i) - y_i)^2\]

• 모델의 예측 결과 \(f(\mathbf{x})\)와 정답 \(y\)를 비교
  • 부호에 상관 없는 결과를 위해 제곱
  • 데이터 개수에 상관 없는 결과를 위해 \(m\)으로 나눔

\[E(f; \mathcal{D}) = \int_{\mathbf{x} \sim \mathcal{D}}(f(\mathbf{x}) - y)^2p(\mathbf{x})d\mathbf{x}\]

• 데이터 분포 \(\mathcal{D}\)와 확률밀도 함수 \(p()\)로 표현

오차율과 정확도

• 오차율: 전체에서 잘못 분류한 샘플의 수

  \[E(f; D) = \frac{1}{m} \sum_{i=1}^m \mathbb{I}(f(\mathbf{x}_i) \neq y_i)\]

  • 확률 밀도 함수

    \[E(f; \mathcal{D}) = \int_{\mathbf{x} \sim \mathcal{D}}\mathbb{I}(f(\mathbf{x}) \neq y)p(\mathbf{x})d\mathbf{x}\]

• 정확도: 전체에서 정확히 분류한 샘플의 수, 1 - 오차율

  \[\begin{align*} acc(f; D) & = \frac{1}{m} \sum_{i=1}^m \mathbb{I}(f(\mathbf{x}_i) = y_i) \\ & = 1 - E(f; D) \end{align*}\]

  • 확률 밀도 함수

    \[\begin{align*} acc(f; \mathcal{D}) & = \int_{\mathbf{x} \sim \mathcal{D}}\mathbb{I}(f(\mathbf{x}) = y)p(\mathbf{x})d\mathbf{x}\\ & = 1 - E(f; \mathcal{D}) \end{align*}\]

재현율, 정밀도, F1 스코어

• 오차율만으로는 자세한 정보를 알기 어려움
  • 예) 잘못 분류한 샘플이 위양성인지, 위음성인지

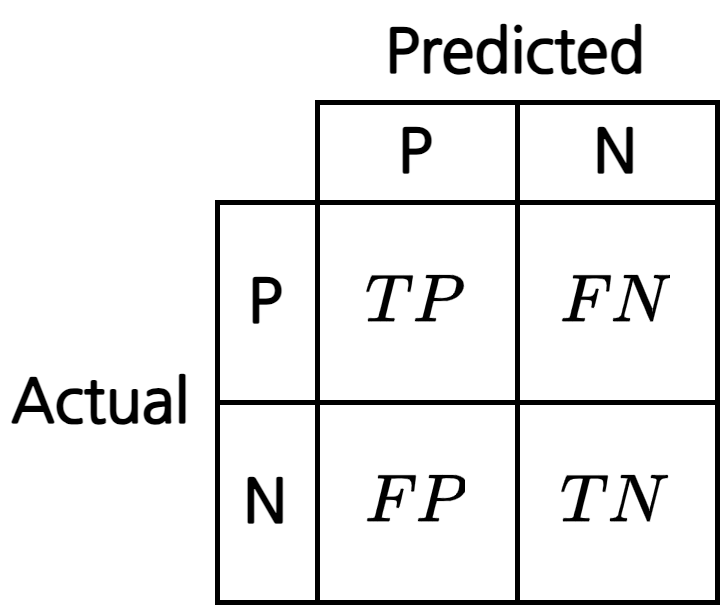
• 혼동 행렬(confusion matrix): 이진 분류 문제에서 실제 클래스와 모델이 예측 분류한 클래스의 조합

  

  • 해석하는 방법: \(T\),\(F\)는 정답 여부, \(P\),\(N\)은 예측한 결과
    • \(T\): 정답을 맞춤, \(F\): 정답을 틀림
    • \(P\): 예측한 결과가 양성, \(N\): 예측한 결과가 음성
  • \(TP\): 진양성(true positive), 예측은 양성이고 실제도 양성
  • \(TN\): 진음성(true negative), 예측은 음성이고 실제도 음성
  • \(FP\): 위양성(false positive), 예측은 양성인데 실제는 음성
  • \(FN\): 위음성(false negative), 예측은 음성인데 실제는 양성

• 정밀도(precision): 양성으로 예측한 것 중 실제 양성의 비율

  \[P = \frac{TP}{TP + FP}\]

• 재현율(recall): 실제 양성 중 양성으로 잘 예측한 비율

  \[R = \frac{TP}{TP + FN}\]
• 정밀도와 재현율은 trade-off 관계
  • 모두 양성으로 분류한다면
    • 실제 양성 모두를 양성으로 분류하므로 재현율은 높아지지만
    • 양성이 아닌 것 까지 양성으로 분류하기 때문에 정밀도는 낮아짐
  • 너무 신중하게 양성을 고른다면
    • 양성이 아닌 것을 양성으로 분류하는 경우는 적어지므로 정밀도는 높아지지만
    • 양성인 것을 음성으로 분류하는 경우가 많아지므로 재현율은 낮아짐
• 손익분기점(break-even point, BEP): ‘정밀도 = 재현율’일 때의 값
  • BEP를 비교하여 어떤 모델의 성능이 좋은지 알 수 있음

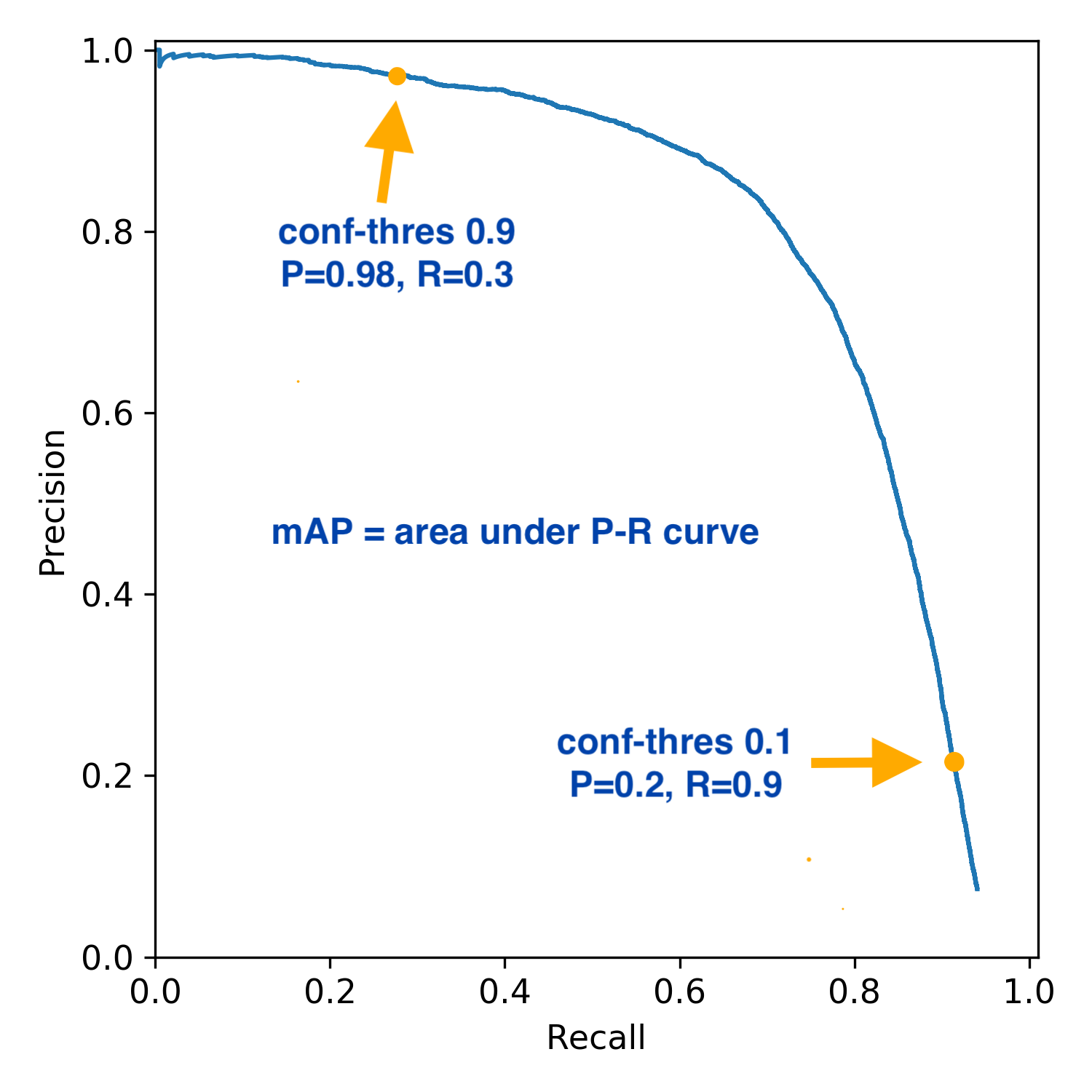
• P-R 곡선(P-R Curve): \(x\)축을 재현율로, \(y\)축을 정밀도로 설정한 곡선

  

  • p-r curve 그리는 방법
    • 모델을 통해 얻은 결과(\([0.0, 1.0]\))를 오름차순으로 정렬
    • 임계값을 0.0부터 점차 올리며 재현율과 정밀도를 계산해 점으로 표시
      • 임계값이 0.0인 경우
        • 모든 결과를 positive로 판단
        • 재현율: \(FN\)이 없으므로 1.0
        • 정밀도: \(FP\)가 매우 크므로 대략 0.5(정답 중 p의 비율을 따름)
      • 임계값이 1.0인 경우
        • 모든 결과를 negative로 판단(예측값이 정확히 1.0이 되는 경우는 거의 없음)
        • 재현율: \(FN\)이 매우 크고 \(TP\)가 0이므로 0.0
        • 정밀도: \(TP\)가 0이고 \(FP\)도 0이므로 \(\frac{0}{0}\), 정밀도의 목적은 \(FP\)를 줄이는 것이므로 1.0으로 생각
  • A 모델이 B 모델의 그래프 영역에 완전히 포함된다면 B 모델이 A 모델보다 훌륭하다고 할 수 있음
  • 교차한다면 비교하기 어렵지만 일반적으로 영역의 넓이를 비교하거나 BEP를 비교

• F1 스코어: 재현율과 정밀도의 조화 평균(\(\frac{1}{F1} = \frac{1}{2} \cdot \left( \frac{1}{P} + \frac{1}{R} \right)\)) \(\begin{align*} F1 &= \frac{2\times P \times R}{P + R}\\ &= \frac{2\frac{TP}{TP + FP}\frac{TP}{TP + FN}}{\frac{TP}{TP + FP} + \frac{TP}{TP + FN}}\\ &= \frac{2\frac{TP}{(TP + FP)(TP + FN)}}{\frac{2TP + FP + FN}{(TP + FP)(TP + FN)}}\\ &= \frac{2TP}{2TP + FP + FN}\\ &= \frac{2 \times TP}{m + TP - TN} & (\because TP + FP + FN = m - TN)\\ \end{align*}\)

  • 문제에 따라 정밀도와 재현율의 중요도는 다름
    • 추천 시스템은 정밀도가 중요
    • 종양의 양,음성 여부는 재현율이 중요

  • 따라서 F1의 일반 형식은 \(F_\beta\)를 이용해 정밀도와 재현율에 대한 서로 다른 선호도를 나타낼 수 있음

    \[F_\beta = \frac{(1 + \beta^2) \times P \times R}{(\beta^2 \times P) + R}, \; \beta \gt 0\]
    • 가중 조화 평균(\(\frac{1}{F_\beta} = \frac{1}{1 + \beta^2} \cdot \left( \frac{1}{P} + \frac{\beta^2}{R} \right)\))
    • \(\beta \lt 1\): 정밀도의 영향이 큼
    • \(\beta = 1\): F1 스코어
    • \(\beta \gt 1\): 재현율의 영향이 큼
• 여러 번의 훈련이나 테스트를 실행하거나 여러개의 데이터셋을 사용하여 많은 수의 혼동 행렬을 얻은 경우
  • 매크로 F1(macro-F1)
    • 각 혼동 행렬의 정밀도와 재현율을 평균내어 계산

    • 매크로 정밀도

      \[\text{macro-}P = \frac{1}{n}\sum_{i=1}^n P_i\]

    • 매크로 재현율

      \[\text{macro-}R = \frac{1}{n}\sum_{i=1}^n R_i\]

    • 매크로 F1

      \[\text{macro-}F1 = \frac{2 \times \text{macro-}P \times \text{macro-}R}{\text{macro-}P + \text{macro-}R}\]
  • 마이크로 F1(micro-F1)
    • 모든 혼동 행렬의 원소들을 평균내어 정밀도와 재현율을 계산

    • 마이크로 정밀도

      \[\text{micro-}P = \frac{\overline{TP}}{\overline{TP} + \overline{FP}}\]

    • 마이크로 재현율

      \[\text{micro-}R = \frac{\overline{TP}}{\overline{TP} + \overline{FN}}\]

    • 마이크로 F1

      \[\text{micro-}F1 = \frac{2 \times \text{micro-}P \times \text{micro-}R}{\text{micro-}P + \text{micro-}R}\]

ROC, AUC

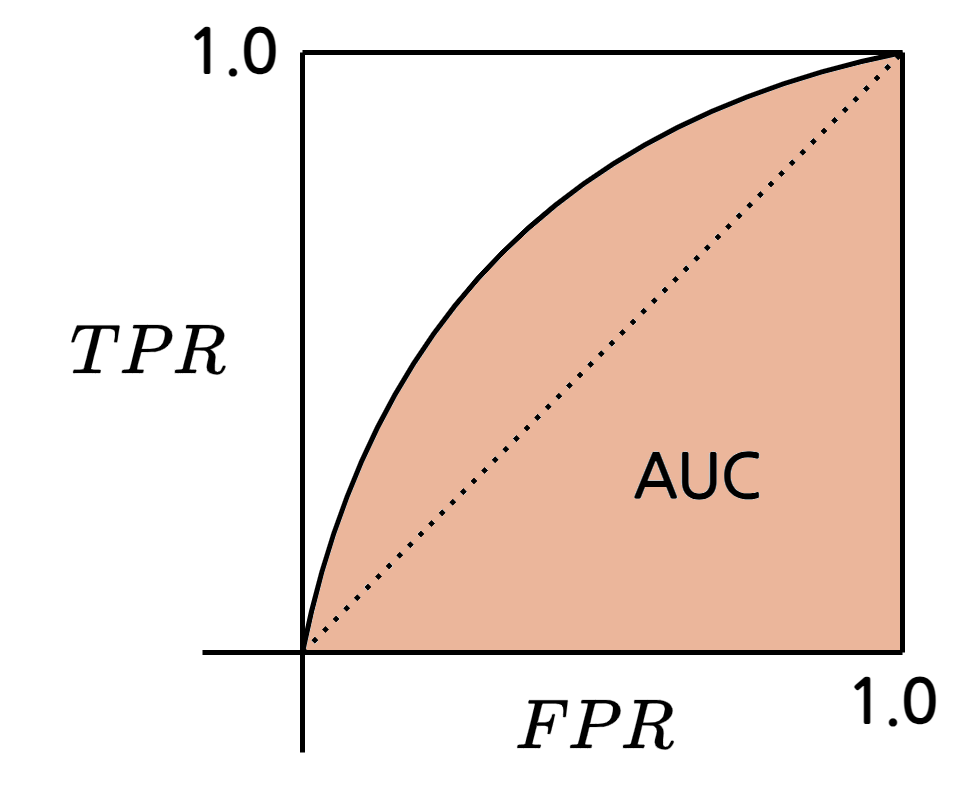
ROC(Receiver Operating Characteristic)

• 모델의 일반화 성능을 연구하기 위한 도구
• P-R 곡선과 비슷하게 예측 결과를 기반으로 순서를 매겨 계산
• \(x\)축에 \(FPR\)을, \(y\)축에 \(TPR\)을 그려 곡선 생성

  • \(TPR\): 참 양성률(True Positive Rate)

    \[TPR = \frac{TP}{TP + FN}\]

  • \(FPR\): 거짓 양성률(False Positive Rate)

    \[FPR = \frac{FP}{TN + FP}\]
• 그림에서 대각선은 랜덤 예측 모델을 의미
• P-R 곡선과 비슷하게 영역의 넓이(AUC, Area Under Curve)로 모델의 우열을 나눌 수 있음
  • 완벽한 모델의 경우 \((0, 1)\)을 지남
• 실제 경우에는 데이터의 수가 한정되어 있으므로 완전한 곡선이 나오기 어려움
  • 따라서 근사 곡선을 그려 판단
• AUC 구하기
  • ROC 곡선의 각 좌표를 \(\{(x_1, y_1), (x_2, y_2), ..., (x_m, y_m)\}\)로 설정
  \[AUC = \frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1} - x_i)(y_i + y_{i+1})\]