확률 및 통계학 2. 대표값과 기술통계

대표값(representative value)

• 데이터를 대표할 수 있는 값
• 평균, 중앙값, 최빈값, 중앙범위 등이 있음

평균(mean, average)

\[\text{average} = \frac{\text{sum}}{\text{count}}\]

• 평균 = (데이터의 합) / (데이터의 개수)
• 모평균(\(\mu\)): 모집단의 평균
• 표본평균(\(\bar{x}\)): 표본의 평균
• 평균의 단점

  • 이상치(outlier)의 영향을 받음

    \[\begin{matrix} 1 & 1 & 2 & 3 & 100 \end{matrix}\]
    • 평균: \(\frac{1 + 1 + 2 + 3 + 100}{5}=21.4\)
    • 대부분 1, 2, 3이지만 이상치 100 때문에 평균이 커짐

중앙값(median)

• 크기순으로 배열 했을 때 중간에 위치한 값
  • \(n\)이 홀수: \(\frac{n+1}{2}\)번째
  • \(n\)이 짝수: \(\frac{n}{2}\)번째와 \(\frac{n}{2}+1\)번째의 평균
• 이상치의 영향을 거의 받지 않음

• 예)

  \[\begin{matrix} 1 & 1 & 2 & 3 & 100 \end{matrix}\]
  • \(n=5\)이므로 \(\frac{5+1}{2}=3\), 3번째 값인 2가 중앙값

최빈값(mode)

• 가장 빈도가 많은 값
• 질적 자료에 사용
• 최빈값이 2개일 경우 이봉자료라고 함

• 예)

  \[\begin{matrix} 1 & 1 & 2 & 3 & 100 \end{matrix}\]
  • 가장 많이 관측되는 값: 1

중앙범위(central range)

\[\text{midrange}=\frac{\text{max} + \text{min}}{2}\]

• 중앙범위 =최대값과 최소값의 평균

• 예)

  \[\begin{matrix} 1 & 1 & 2 & 3 & 100 \end{matrix}\]
  • 중앙값: \(\frac{1 + 100}{2} = 50.5\)

백분위수(percentile)

• 위치점 \(p\%\): 비율 \(p\)만큼이 그 값보다 작고 \((1-p)\)만큼이 큰 값
• 백분위수 \(p_n\): 위치점 \(n\%\)

• 예)

  \[\begin{array}{c|cccccccc} 3 & 4 & 4 & 6 & 9\\ 4 & 3 & 6 & 7 & 8 & 9\\ 5 & 0 & 1 & 1 & 5 & 7 & 7 & 8 & 9\\ 6 & 0 & 0 & 4 & 4 & 7\\ 7 & 1 & 5 & 8 & 8 & 8 & 9\\ 8 & 4 & 6 & 8 & 8\\ \end{array}\]
  • 백분위수 \(p_{25}\)
    • \(32개 \times 25\%=8\), 8번째 수: 48
    • \(32개 \times 75\%=24\), 24번째 수: 49
    • 따라서 \(p_{25} = \frac{48 + 49}{2} = 48.5\)
  • \(개수 \times p\%\) 했을 때 정수면 \((1-p)\%\)​도 계산, (정수가 아닌) 실수면 올림만 하면 됨

사분위수(quantile)

• 제1사분위수(\(Q_1\)): \(p_{25}\)
• 제2사분위수(\(Q_2\)): \(\bar{x}\), \(p_{50}\)
• 제3사분위수(\(Q_3\)): \(p_{75}\)

십분위수(decile)

• 제1십분위수(\(D_1\)), 제2십분위수(\(D_2\)), …, 제9십분위수(\(D_9\))
• \(D_1 = p_{10}\), \(D_2 = p_{20}\), …, \(D_9 = p_{90}\)

산포도(scatter)

• 자료들이 대표값 주위에서 어느 정도 분포되어 있는지를 나타내는 통계값

범위(range)

\[R = \max - \min\]

• 범위 = 최댓값 - 최솟값

• 사분위수의 범위(\(IQR\))

  \[IQR = Q_3 - Q_1\]

분산(variance)

• 모집단 분산

  \[\sigma^2=\frac{\sum_{i+1}^{N}(x_i-\mu)^2}{N}\]
  • \(N\): 모수의 개수
  • \(x_i-\mu\): 편차

  • 간편식

    \[\sum_{i=1}^{k}f_i(x_i^\ast-\mu)^2=\sum_{i=1}^{k}f_ix_i^{\ast2}-N\mu^2\]
    • \(f_i\): \(x_i\)의 빈도

• 표본 분산

  \[s^2=\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}\]
  • 모분산과 비슷하게 하기 위해 \(n\)이 아닌 \(n-1\)로 나눔

• 도수분포표에서의 근사 분산

  \[\sigma^2=\frac{\sum_{i+1}^{N}f_i(x_i^\ast-\mu)^2}{N}\]

체비셰프 정리(Chebyshev Inequality)

• 분포 상관 없이, 적어도 \((1-\frac{1}{k^2})\cdot 100\%\)의 자료가 \(\mu \pm k\sigma\) 사이에 존재
• 예)

  • 전체의 \(90\%\), \(\bar{x}=0.26\), \(s=0.005\)

    \[\begin{align*} & 1-\frac{1}{k^2}=0.9\\ & k=\sqrt{10} \simeq 3.16\\ \end{align*}\]
    • \(0.26 \pm 3.16\times0.005\) 범위에 \(90\%\)의 자료가 존재

  • 적어도 몇 \(\%\)가 0.20, 0.32 사이에 존재

    • 0.20과 0.32의 평균이 \(0.26 = \bar{x}\)이므로 둘 중 하나면 계산하면 됨
    \[\begin{align*} & 0.26 - k\times 0.005 = 0.20\\ & k=12\\ & 1-\frac{1}{k^2}\simeq0.99305\\ \end{align*}\]
    • \(99.305\%\) 사이에 존재

변이 계수(coefficient of variation)

\[V_c=\frac{s}{\bar{x}}\times 100\%\]

• \(V_c\): 변이 계수
• \(V_c^2\): 상대 분산
• 변이 계수가 높을 수록 변동성이 높다는 의미
• 예)
  • A주식: 76,300, 77,400, 77,900, 77,200, 76,900, 78,800
    • \(\bar{x}=77416.6669\), \(s=861\)​
    • 변이 계수: \(V_c = \frac{861}{77417}\times 100 = 1.1121\)
  • B주식: 6,400, 7,000, 7,400, 6,900, 7,300, 7,600
    • \(\bar{x}=7100\), \(s=429\)
    • 변이 계수: \(V_c = \frac{429}{7100} \times 100 = 6.0422\)
  • B주식의 변동성이 A주식보다 높음

왜도(skewness)와 첨도(kurtosis)

• 왜도(\(a_3\))

  \[a_3=\frac{\mu^3}{\sigma^3}\]
  • 비대칭성의 의미
    • \(a_3\lt 0\): 좌측에 치우쳐짐
    • \(a_3\gt 0\): 우측에 치우쳐짐

• 첨도(\(a_4\))

  \[a_4=\frac{\mu^4}{\sigma^4}\]
  • \(a_4 \lt 3\): 완첨(완만)
  • \(a_4 \gt 3\): 급첨(뾰족)

표준점수(z-score)

\[Z=\frac{x_i - \mu}{\sigma}\]

• 자료의 \(i\)번째 측정값 \(x_i\)의 표준점수
• 표준점수는 단위를 없애주기 때문에 서로 다른 자료를 비교하기에 용이
• 예)
  • A의 점수: 700점, \(\mu\): 500점, \(\sigma\): 100점
    • 표준점수: \(Z=\frac{700 - 500}{100}=2\)
  • B의 점수: 24점, \(\mu\): 18점, \(\sigma\): 6점
    • 표준점수: \(Z=\frac{24 - 18}{6}=1\)
  • A가 B보다 시험을 잘봄

이상치 검출

• 이상치(outlier): 일반적이지 않은 값
  • 데이터의 일반적인 범위에서 벗어난 값

• 일반적으로 \(Q_1 - 1.5IQR\)보다 작거나 \(Q_3 + 1.5IQR\)보다 크면 이상치

• 예)

  \[\begin{matrix} 12.81 & 14.95 & 15.83 & 15.97 & 19.90\\ 18.34 & 19.82 & 19.94 & 20.62 & 36.73\\ 20.88 & 20.93 & 20.98 & 21.15 & 22.24\\ 23.16 & 22.24 & 23.16 & 23.56 & 35.78\\ \end{matrix}\]
  • \(Q_1 = \frac{18.34 + 19.82}{2} = 19.08\), \(Q_3=\frac{23.16 + 22.24}{2} = 22.70\), \(IQR = 22.70 - 19.08 = 3.62\)
  • \(Q_1 - 1.5IQR = 19.08 - 5.43 = 13.65\), \(Q_3 + 1.5IQR = 22.70 + 5.43 = 28.13\)
  • 따라서 \(12.81\)과 \(35.78\), \(36.73\)은 이상치

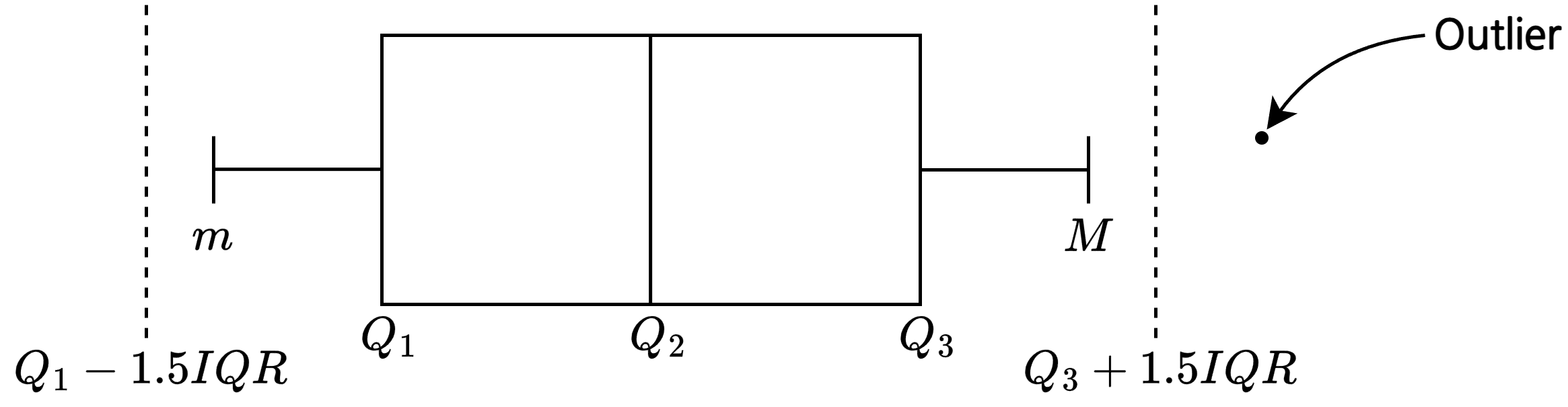
상자그림(box plot)

• 사분위수와 측정값의 최대값, 최소값을 이용해 그린 그림
  • 주식 차트에서 볼 수 있음

• 그리는 방법

  1. \(M\)(최대값)과 \(m\)​(최소값)을 탐색
     • 혹시 이상치일 수도 있으니 2, 3개씩 탐색
  2. \(Q_1\), \(Q_2\), \(Q_3\), \(IQR\), \(Q_1 - 1.5IQR\), \(Q_3 + 1.5IQR\) 계산
  3. 2를 바탕으로 이상치 탐색

  4. 상자 그림에 표시

     

     • 주의: \(Q_2\)는 비율에 따른 위치에 그려야 함(\(Q_1=1\), \(Q_2=2\), \(Q_3=4\)이라면 \(Q_2\)는 \(Q_1\)과 \(Q_3\)를 \(1:2\)로 내분하는 곳에 위치)
  5. 이상치에 대한 정보 서술
     • 있는 경우: “이 자료에는 \(n\)개의 이상치(\(a\), \(b\), …)가 존재한다.”
     • 없는 경우: “이 자료에는 이상치가 없다.”

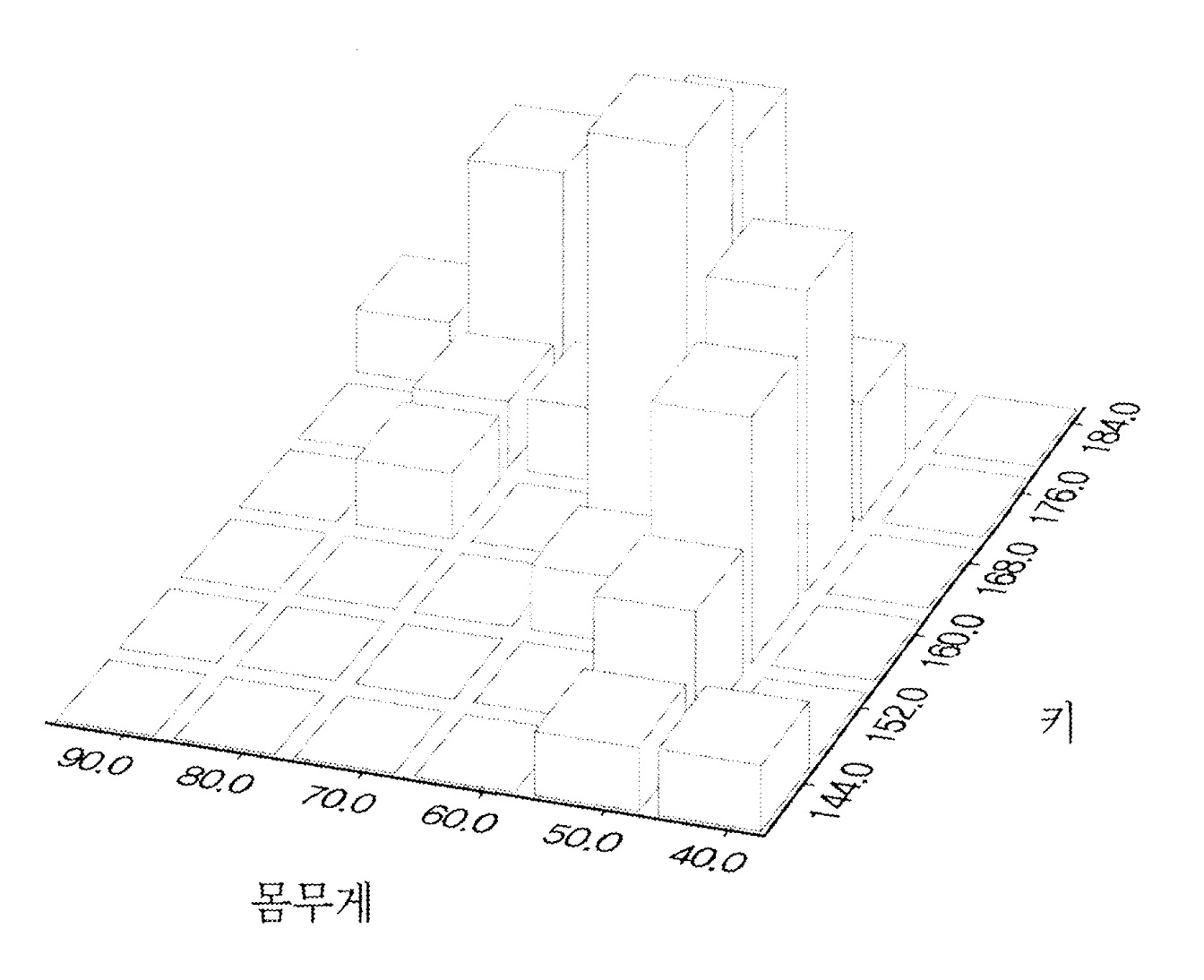
이변량 자료의 분석

• 이변량 자료: 변수가 2개인 자료

• 2차원 히스토그램

  

• 산점도(scatter)

  

• 리그레쏘그램(regressogram)

  

상관 분석

• 공분산

  \[s_{XY}=\frac{1}{n-1}\sum(x_i - \bar{x})(y_i - \bar{y})\]

• 표본상관계수

  \[\begin{align*} r_{XY} & = \frac{s_{XY}}{s_X s_Y}\\ & = \frac{1}{n-1}\sum(\frac{x_i - \bar{x}}{s_X})(\frac{y_i - \bar{y}}{s_Y})\\ & = \frac{\sum(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum(x_i - \bar{x})^2 \sum(y_i - \bar{y})^2}} \end{align*}\]
  • \(r_{XY}\)이 1에 가까울 수록 선형
  • $-1 \le r_{XY} \le 1$
    • \(-1 \le r_{XY} \lt 0\): \(x\)가 증가할 때, \(y\) 감소
    • \(r_{XY} = 0\): 선형성 없음
    • \(0 \lt r_{XY} \le 1\): \(x\)가 증가할 때, \(y\) 증가

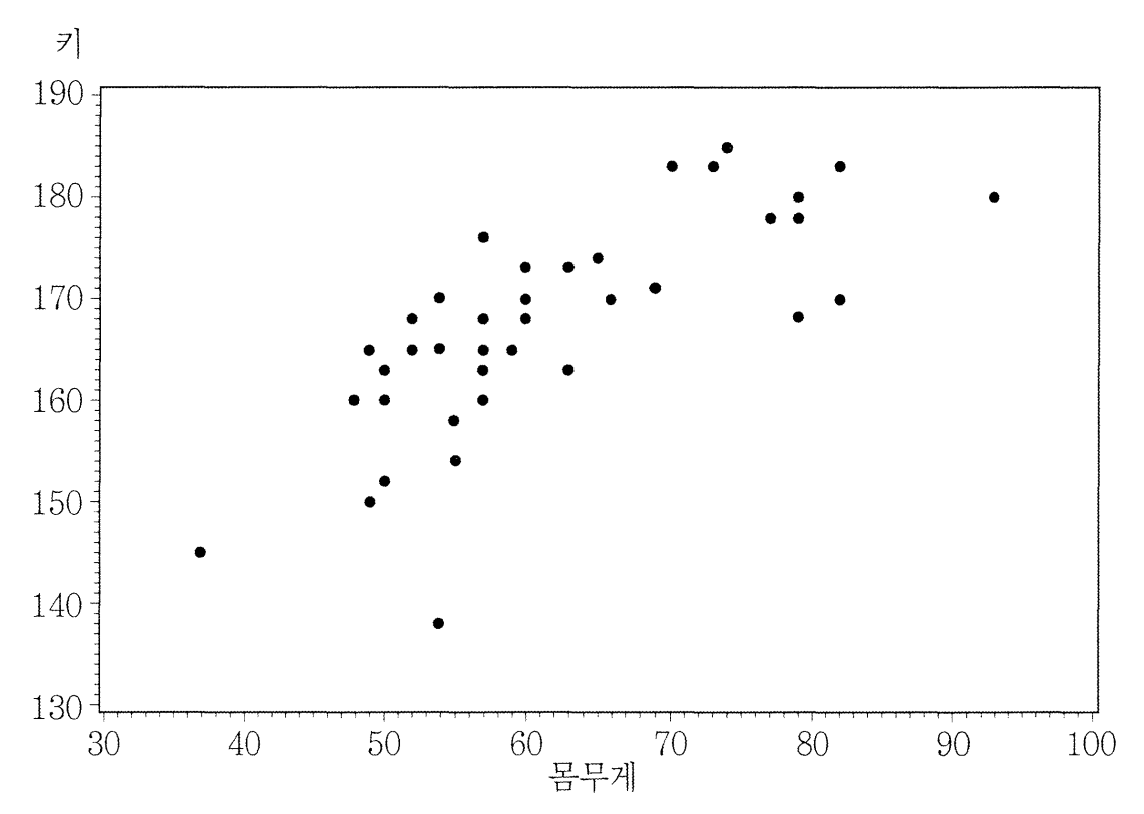
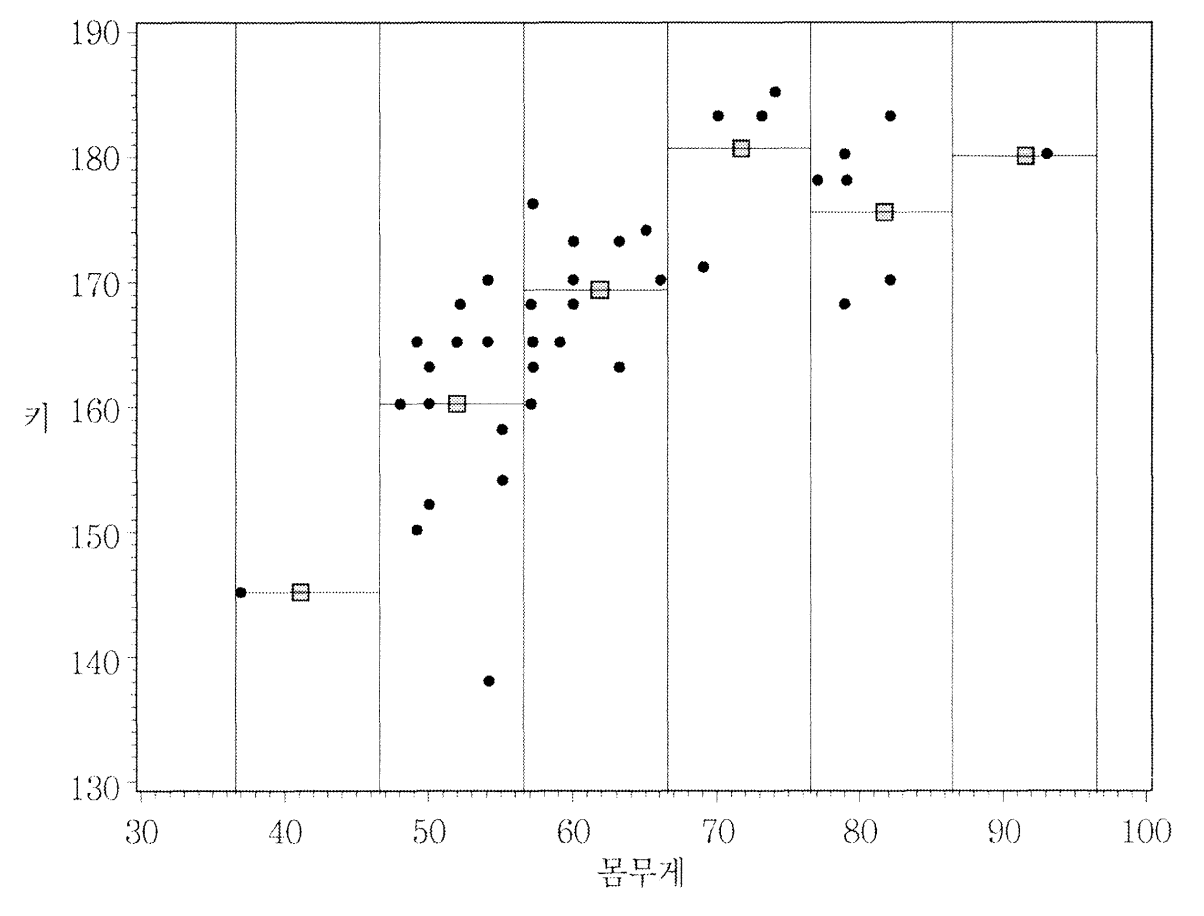
  • 예)

    \[\begin{array}{c|cccccccccc} X & 3 & 6 & 5 & 2 & 7 & 8 & 5 & 3 & 6 & 5\\ \hline Y & 70 & 80 & 75 & 65 & 70 & 95 & 80 & 70 & 85 & 80\\ \end{array}\]
    • 평균: \(\bar{x}=5\), \(\bar{y}=77\)
    • 표준편차: \(s_X=1.886\), \(s_Y=8.882\)
    • 공분산: \(S_{XY}=12.778\)
    • 표본상관계수: \(r_{XY}=\frac{s_{XY}}{s_X s_Y}=0.763\)
      • 상관계수가 0.763으로 양의 상관계수이므로 두 변량 사이에 상력한 양의 상관관계가 있다.