확률 및 통계학 3. 확률과 확률분포
사건의 확률
- 시행(trial): 결과가 우연에 의해 결정되는 실험이나 관찰
- 표본공간(sample space, \(\Omega = \{\omega_1, \omega_2, \cdots, \omega_n\}\)): 주어진 시행에서 가능한 모든 결과들의 집합
- 근원사건(elementary event): 표본공간을 구성하는 개개의 결과
- 사건(event): 표본공간의 부분집합
- 전사건: 어떤 사건에서 반드시 일어나는 사건
- 공사건: 시행의 결과가 관측되지 않는 사건
사건 \(A\)의 확률
- \(P(A)\): 한 가지 실험을 반복할 때 \(A\) 사건이 일어나는 횟수의 비율
- 확률의 기본법칙
- 모든 사건 \(A\)에 대해 \(0 \le P(A) \le 1\)
- $P(A) = \sum_{\omega_i \in A} P(\omega_i)$
- $P(\Omega) = \sum_{\omega_i \in \Omega} P(\omega_i) = 1$
확률법칙
- 여사건(\(A^C\)): 사건 \(A\)에 포함되지 않은 근원사건들의 모임
- 합사건(\(A \cup B\)): 사건 \(A\) 또는 \(B\)에 포함되는 근원사건들의 모임
- 곱사건(\(A \cap B\)): 사건 \(A\)와 \(B\)에 동시에 포함되는 근원사건들의 모임
- 배반사건(exclusive events): 두 사건의 공통 원소가 없는 경우, \(A \cap B = \varnothing\)
- 합사건의 법칙: \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
- 여사건의 법칙: \(P(A^C) = 1-P(A)\)
예)
\[\begin{matrix} \text{meterial} & \text{temperature} & \text{pressure}\\ 1 & 1000 & 2\\ 2 & 1000 & 3\\ 3 & 1500 & 2\\ 4 & 1500 & 2\\ \end{matrix}\]- 표본공간(2개 선택): \(\Omega = \{(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)\}\)
- 같은 온도: \(A = \{(1, 2), (3, 4)\}\)
- 같은 압력: \(B = \{(1, 3), (1, 4), (3, 4)\}\)
- 온도와 압력이 모두 다른 사건: \(\Omega - (A \cup B) = \{(2, 3), (2, 4)\}\)
- 온도와 압력이 모두 같은 사건: \(A \cap B = \{(3, 4)\}\)
- 온도는 같고 압력이 다른 사건: \(A - B = A \cap B^C = \{(1, 2)\}\)
- 온도가 다르거나 압력이 같은 사건: \(A^C \cup B = \{(1, 3), (1, 4), (2, 3), (2, 4), (3, 4)\}\)
- 온도나 압력이 같을 확률: \(P(A \cup B) = P(A) + P(B) - P(A \cap B) = \frac{2}{6} + \frac{3}{6} - \frac{1}{6} = \frac{2}{3}\)
- 온도가 다르거나 압력이 다를 확률: \(P(A^C \cup B^C) = 1 - P(A \cap B) = \frac{5}{6}\)
조건부확률
\[P(A \mid B) = \frac{P(A \cap B)}{P(B)}\]- 사건 \(B\)가 일어났을 때, 사건 \(A\)가 일어날 확률
- 곱사건의 법칙: \(P(A \cap B) = P(A \mid B)P(B) = P(B \mid A)P(A)\)
- 독립사상: \(A \perp B \Leftrightarrow P(A \mid B) = P(A) \; or \; P(B \mid A) = P(B)\)
- $P(A \cap B) = P(A) \cdot P(B)$
- 예)
- 20명: 결제일 지킴(\(S\)), 5명: 결제일 안 지킴(\(F\)) -> 임의로 2명을 선택할 때, 한 명은 지키고 한 명안 안 지켰을 확률
- $P(S_1 \cap F_2) + P(F_1 \cap S_2) = P(S_1)P(F_2 \mid S_1) + P(F_1)P(S_2 \mid F_1) = \frac{20}{25} \times \frac{5}{24} + \frac{5}{25} \times \frac{20}{24} = \frac{1}{3}$
- 20명: 결제일 지킴(\(S\)), 5명: 결제일 안 지킴(\(F\)) -> 임의로 2명을 선택할 때, 한 명은 지키고 한 명안 안 지켰을 확률
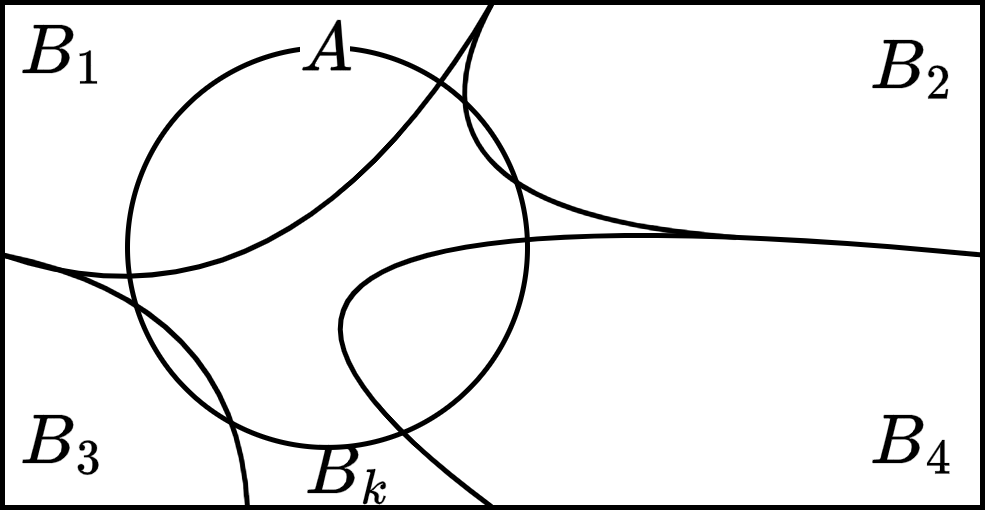
표본공간 \(\Omega\)의 분할
- \(B_i \cap B_j = \varnothing\), \(\Omega = B_1 \cup B_2 \cup \cdots \cup B_k\)이면 \(B_1, B_2, \cdots , B_k\)를 표본공간의 분할이라고 함
- 전확률의 정리: \(P(A) = P(B_1) \cdot P(A \mid B_1) + P(B_2) \cdot P(A \mid B_2) + \cdots + P(B_k) \cdot P(A \mid B_k)\)
베이즈 정리
\[P(B_i \mid A) = \frac{P(B_i) \cdot P(A \mid B_i)}{P(B_1) \cdot P(A \mid B_1) + P(B_2) \cdot P(A \mid B_2) + \cdots + P(B_k) \cdot P(A \mid B_k)}\]예)
\[\begin{matrix} \text{factory} & \text{ratio} & \text{defect rate}\\ A_1 & 30\% & 2\%\\ A_2 & 50\% & 1\%\\ A_3 & 20\% & 5\%\\ \end{matrix}\]세 공장의 제품 중 하나를 골랐을 때 불량일 확률
\[\begin{align*} P(A) &= P(A_1) \cdot P(A \mid A_1) + P(A_2) \cdot P(A \mid A_2) + P(A_3) \cdot P(A \mid A_3)\\ &= 0.3 \cdot 0.02 + 0.5 \cdot 0.01 + 0.2 \cdot 0.05\\ &= 0.021\\ \end{align*}\]불량이 발생했을 때, \(A_1\) 공장에서 발생했을 확률
\[P(A_1 \mid A) = \frac{P(A \cap A_1)}{P(A)} = \frac{P(A_1) \cdot P(A \mid A_1)}{P(A)} = \frac{0.3 \cdot 0.02}{0.021}\]
확률 변수
- 확률 변수(random variable, \(X\)): 각각의 근원사건들에 실수값을 대응시키는 함수
- 이산 확률 변수(discrete random variable): 확률 변수가 가질 수 있는 값이 이산적인 경우
- 연속 확률 변수(continuous random variable): 확률 변수가 가질 수 있는 값이 연속적인 경우
- 확률 분포(probability distribution): 확률 변수가 가질 수 있는 값에 확률을 대응시킨 관계
- 확률 함수(probability function): 확률 변수의 각 값에 확률을 대응시키는 함수
이산 확률 변수
- 확률 질량 함수(probability mass function, pmf): \(P(X = x_i) = p(x_i)\)
- \(0 \le p(x_i) \le 1\), \(i = 1, 2, \cdots , n\)
- $\sum_{i=1}^n p(x_i) = 1$
- $P(a \lt X \le b) = \sum_{a \lt x \le b} P(X = x)$
- 이산 확률 변수의 기대값
- 평균: \(E(X) = \mu = \sum_x xp(x)\)
- $E(a) = a$
- $E(aX) = aE(X)$
- $E(a + bX) = a + bE(X)$
- $E(aX + bY) = aE(X) + bE(Y)$
- 분산: \(Var(X) = E(X - \mu)^2 = \sum_x (x - \mu)^2 p(x) = \sum_x^n x^2 p(x) - \mu^2 = E(X^2) - (E(X))^2\)
- $V(a) = 0$
- $V(aX) = a^2 V(X)$
- $V(a + bX) = b^2V(X)$
- 표준 편차: \(sd(X) = \sqrt{Var(X)}\)
- 평균: \(E(X) = \mu = \sum_x xp(x)\)
연속 확률 변수
- 확률 밀도 함수(probability density function, pdf): \(f(x)\)
- 모든 \(x\)에 대해, \(f(x) \ge 0\)
- $P(a \le X \le b) = \int_a^b f(x)dx$
- $P(-\infty \lt X \lt \infty) = \int_{-\infty}^{\infty} f(x) dx = 1$
- 연속 확률 변수의 기대값
- 평균: \(E(X) = \int_{-\infty}^{\infty} xf(x) dx = \mu\)
- 분산: \(Var(X) = \int_{-\infty}^{\infty} (x - \mu)^2 f(x) dx = \sigma^2\)
- 표준 편차: \(sd(X) = \sqrt{Var(X)} = \sigma\)
이산 확률 분포
이항 분포
- 베르누이 실험: \(\Omega = \{0, 1 \}\)
- 성공과 실패로만 결과가 나오는 실험
- 베르누이 시행: 확률이 \(p\)로 일정한 베르누이 실험을 \(n\)번 반복하는 시행
- 상호 배반
- 서로 독립
- 이항 실험: 베르누이 시행에서 성공 횟수를 세는 실험

확률 변수 \(X\): \(X \sim Bin(n, p)\)
확률 질량 함수
\[P(X) = \binom{n}{p} p^x q^{n-x}, \; x= 0, 1, \dots, n\]- \(p = 0.5\): 대칭
- \(p\lt 0.5\): 오른쪽 꼬리
- \(p \gt 0.5\): 왼쪽 꼬리
평균: \(E(X) = np\)
분산: \(Var(X) = npq\)
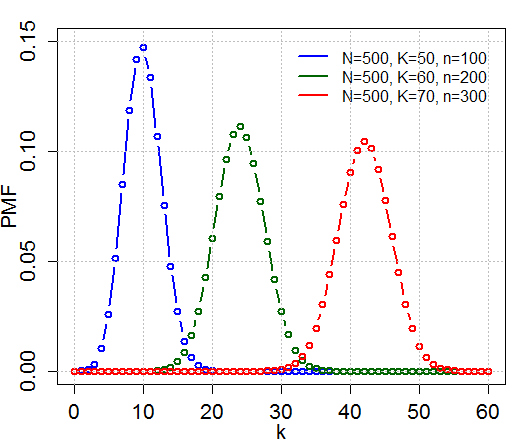
초기하 분포
- 비복원 추출에서 \(N_1\)개의 목표가 포함된 \(N\)개의 모집단 중 \(n\)개를 추출할 때, 성공 횟수에 대한 확률 분포
- 상호 배반
- 비독립적
- 예) 공을 뽑을 때, 공을 다시 넣지 않고 계속 추출
 By Fuzzyrandom - Own work, CC BY-SA 4.0
By Fuzzyrandom - Own work, CC BY-SA 4.0
확률 변수 \(X\): \(X \sim Hypgeom(n, N_1, N)\)
확률 질량 함수
\[P(X)=\frac{\binom{N_1}{x} \binom{N - N_1}{n - x}}{\binom{N}{n}}, \; x = \max(0, n - N + N_1), \dots, \min(n, N_1)\]- 평균: \(E(X) = n\frac{N_1}{N}\)
- \(p\)를 \(\frac{N_1}{N}\)로 생각
분산: \(Var(X) = npq\left(\frac{N-n}{N-1}\right) = n \left(\frac{N_1}{N}\right) \left(1 - \frac{N_1}{N}\right) \left(\frac{N-n}{N-1}\right)\)
- 초기하 분포 -> 이항 분포 근사
- \(n \lt 0.005N\)이면 이항분포로 생각할 수 있음
포아송 분포
- 단위 시간당 평균 발생률이 \(\lambda\)인 사건의 발생 횟수

확률 변수 \(X\): \(X \sim Po(\lambda)\)
확률 질량 함수
\[P(X)=\frac{e^{-\lambda}\lambda^x}{x!}\]- 평균: \(E(X) = \lambda\)
- 분산: \(Var(X) = \lambda\)
- 이항 분포 -> 포아송 분포 근사
- \(n \ge 100\)이고 \(\lambda = E(X) = np \le 5\)이면 \(Bin(n, p) = Po(np)\)로 생각할 수 있음
연속 확률 분포
균등 분포
- 확률 변수 \(X\): \(X \sim U(a, b)\)
확률 밀도 함수
\[f(x) = \begin{cases} \frac{1}{b - a}, & a \le x \le b \\ 0, & x \lt a \; or \; x \gt b \end{cases}\]- 평균: \(E(X) = \frac{a + b}{2}\)
- 분산: \(Var(X) = \frac{(b - a)^2}{12}\)
정규 분포
- 확률 변수 \(X\): \(X \sim N(\mu, \sigma^2)\)
확률 밀도 함수
\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x - \mu)^2}{2\sigma^2}}, \; -\infty \lt x \lt \infty\]- 정규 분포 확률 밀도 함수의 특징
- 종 모양
- 아래쪽 영역의 총면적은 항상 1
- 평균은 함수의 중앙에 위치하며, 평균에 대해 좌우 대칭이고, 평균에서 최댓값
- 평균, 중위수, 최빈값은 모두 같은 값
- 정규 분포의 모양과 위치는 평균과 표준편차에 의해 달라짐
- 이항 분포 -> 정규 분포
- \(np \gt 5\)이고, \(nq \gt 5\)이면 \(X \sim N(np, npq)\)로 생각할 수 있음
연속성 수정: 이산형 분포를 연속형으로 근사할 때 양 끝이 버려져 발생하는 오차를 해결하는 방법
\[P(a \le X \le b) \rightarrow P(a - 0.5 \le X \le b + 0.5)\]
표준 정규 분포
- 확률 변수 \(Z\): \(Z = \frac{X - \mu}{\sigma} \sim N(0, 1)\)
- 정규 분포를 z-score에 대입하여 변환한 정규 분포
- 서로 다른 평균과 표준편차를 가진 정규 분포를 비교할 수 있도록 해줌
This post is licensed under CC BY 4.0 by the author.