확률 및 통계학 5. 추정과 가설 검정

추정

• 추정: 표본의 정보를 이용하여 모집단의 모수를 추론하는 방법
• 추정량(\(\hat{\theta}\)​): 추정을 통해 추론한 모수, hat 기호를 이용해 표기
• 추정 오차: 모수와 추정량 사이의 차
• 신뢰수준: \(1 - \alpha\)만큼 신뢰할 수 있다는 의미
  • 예) \(95\%\)(\(0.95\))만큼 신뢰할 수 있다면 \(1 - \alpha = 0.95\), \(\alpha = 0.05\)
• 임계값(\(z_\alpha\)): 표준정규곡선에서 오른쪽 고리부분의 면적이 \(\alpha\)에 해당하는 지점의 값
  • 예) \(z_{0.025} = 1.96\)
  • 대표본(\(n \ge 30\))인 경우: \(z_\alpha\)
  • 소표본(\(n \lt 30\))인 경우: 자유도가 \(n - 1\)인 t-분포에서 정의된 \(t_\alpha\)​
• 추정의 종류
  • 점추정: 정확한 값을 추정
  • 구간추정: 대략적인 구간을 추정, 신뢰하한과 신뢰상한을 구하는 것이 목표

모평균 \(\mu\)에 대한 추정

점추정

• 모수: \(\mu\)
• 추정량: \(\hat{\mu} = \bar{x}\)
• 표준오차(\(SE(\bar{x}) = \frac{\sigma}{\sqrt{n}}\)): \(\bar{x}\)가 \(\mu\)를 중심으로 어느 정도의 오차를 가지고 산포되어 있는가를 나타내는 기준
  • 만약 \(\sigma\)가 알려져 있지 않고 \(n\)이 크다면 \(\sigma\) 대신 \(s\) 사용 가능(\(\hat{SE}(\bar{x}) = \frac{s}{\sqrt{n}}\))
• 추정오차: \(E = z_{\alpha / 2} SE(\bar{x}) = z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}\)​
  • 예) \(95\%\) 추정오차: \(\alpha = 0.05\), \(z_{\alpha / 2} = 1.96\), \(E = 1.96\frac{\sigma}{\sqrt{n}}\)
• 소표본인 경우: \(E = t_{\alpha / 2} \frac{s}{\sqrt{n}}\)
• 모평균 차이에 대한 점추정
  • 추정량: \(\bar{x}_1 - \bar{x}_2\)
  • 추정오차: \(E = z_{\alpha / 2}\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}\)

구간추정

• \(1 - \alpha\)의 신뢰도를 가지는 구간추정

  \[\bar{x} - z_{\alpha / 2}\frac{\sigma}{\sqrt{n}} \lt \mu \lt \bar{x} + z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}\]
  • \(\mu\)의 \(100(1 - \alpha)\%\) 신뢰구간은 (\(\bar{x} - z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}\), \(\bar{x} + z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}\))
• 모집단이 정규분포를 따르는 경우에 사용 가능

• 소표본인 경우

  \[\bar{x} - t_{\alpha / 2}\frac{s}{\sqrt{n}} \lt \mu \lt \bar{x} + t_{\alpha / 2}\frac{\sigma}{\sqrt{n}}\]

• 유도

  \[\begin{align*} & P(-z_{\alpha / 2} \lt \frac{\bar{x} - \mu}{\sigma / \sqrt{n}} \lt z_{\alpha / 2}) = 1 - \alpha \\ & P(\vert \bar{x} - \mu \vert \lt z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}) = 1 - \alpha \\ & P(\bar{x} - z_{\alpha / 2}\frac{\sigma}{\sqrt{n}} \lt \mu \lt \bar{x} + z_{\alpha / 2}\frac{\sigma}{\sqrt{n}}) = 1 - \alpha \\ \end{align*}\]

• 모평균 차이에 대한 구간추정

  \[(\bar{x}_1 - \bar{x}_2) \pm \sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}\]

  • 참고

    \[z = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}}\]

이항 모집단의 모수 \(p\)에 대한 추정

점추정

• 모수: \(p\)
• 추정량: \(\hat{p}\)
• 추정오차: \(E = z_{\alpha / 2} \sqrt{\hat{p}(1 - \hat{p}) / n}\)
• 모비율 차이에 대한 점추정
  • 추정량: \(\hat{p}_1 - \hat{p}_2\)

  • 추정오차

    \[E = z_{\alpha / 2} \sqrt{\frac{\hat{p}_1(1 - \hat{p}_1)}{n_1} + \frac{\hat{p}_2(1 - \hat{p}_2)}{n_2}}\]

구간추정

\[\hat{p} \pm z_{\alpha / 2} \sqrt{\hat{p}(1 - \hat{p}) / n}\]

• 모비율 차이에 대한 구간추정

  \[(\hat{p}_1 - \hat{p}_2) \pm z_{\alpha / 2} \sqrt{\frac{\hat{p}_1(1 - \hat{p}_1)}{n_1} + \frac{\hat{p}_2(1 - \hat{p}_2)}{n_2}}\]

표본의 크기 \(n\)​ 추정

\[n = \left( z_{\alpha / 2} \frac{\sigma}{E} \right)^2\]

• 추정오차 식을 \(n\)에 대한 식으로 변환한 형태
• 일반적으로 결과 올림

이항 모집단

• \(p\)를 아는 경우

  \[n = \hat{p}(1 - \hat{p})\left(\frac{z_{\alpha / 2}}{E} \right)^2\]

• \(p\)를 모르는 경우

  \[n = \frac{1}{4}\left(\frac{z_{\alpha / 2}}{E} \right)^2\]

\(\chi^2\)​ 분포

• 모분산과 모표준편차에 대한 추론에 사용되는 분포
  • 모분산의 표본분포는 자유도가 \(n - 1\)인 \(\chi^2\) 분포를 따름

\[\chi^2 = \frac{(n - 1) s^2}{\sigma^2} = \frac{\sum(x - \bar{x})^2}{\sigma^2}, \; \because s^2 = \frac{\sum(x - \bar{x})^2}{n - 1}\]

• 모분산 \(\sigma^2\)에 대한 \(1 - \alpha\) 신뢰구간

  \[(L_1, L_2) = (\frac{(n - 1) s^2}{\chi^2_{\alpha / 2}(df)}, \frac{(n - 1) s^2}{\chi^2_{1 - \alpha / 2}(df)})\]
  • 여기서 \(\chi^2_\alpha(df)\)는 \(df\)의 자유도를 같는 \(\chi^2\) 분포라는 의미

가설 검정

• 귀무가설(\(H_0\)): 기존에 알려진 가설
• 대립가설(\(H_1\)): 입증하고자 하는 가설
• 가설 검정 절차
  1. 가설 설정
     • \(H_0\): 모수\(= 3\) vs \(H_1\): 모수\(\lt 3\) or 모수\(\gt 3\) or 모수\(\neq 3\)
     • 단측 검정
       • 모수\(\lt 3\): 좌단측
       • 모수\(\gt 3\): 우단측
     • 양측 검정: 모수\(\neq 3\)
  2. 검정 통계량 계산
     • \(\bar{x}\), \(\sigma\), \(n\), \(p\) 등을 이용해 \(z\) 또는 \(t\) 또는 \(\chi^2\) 계산
  3. 임계값
     • \(\alpha\)를 이용해 \(z_\alpha\) 계산(단측 검정인 경우 \(z_\alpha\), 양측 검정인 경우 \(z_{\alpha / 2}\))
     • 2에서 구한 검정 통계량의 범위 확인
       • 단측 검정인 경우
         • 우단측: \((-\infty, z_\alpha]\)(범위 안), \((z_\alpha, \infty)\)(범위 밖)
         • 좌단측: \((-\infty, -z_\alpha)\)(범위 밖), \([-z_\alpha, \infty)\)(범위 안)
       • 양측 검정인 경우
         • \((-\infty, -z_{\alpha / 2})\)(범위 밖), \([-z_{\alpha / 2}, z_{\alpha / 2}]\)(범위 안), \((z_{\alpha / 2}, \infty)\)(범위 밖)
     • 범위 안이면 \(H_1\) reject
     • 범위 밖이면 \(H_0\) reject
     • 여기서 범위 안을 채택역, 범위 밖을 기각역이라고 함
  4. 결론
     • 유의수준 \(\alpha\) 하에서 ~라는 주장을 할 수 있다/없다.

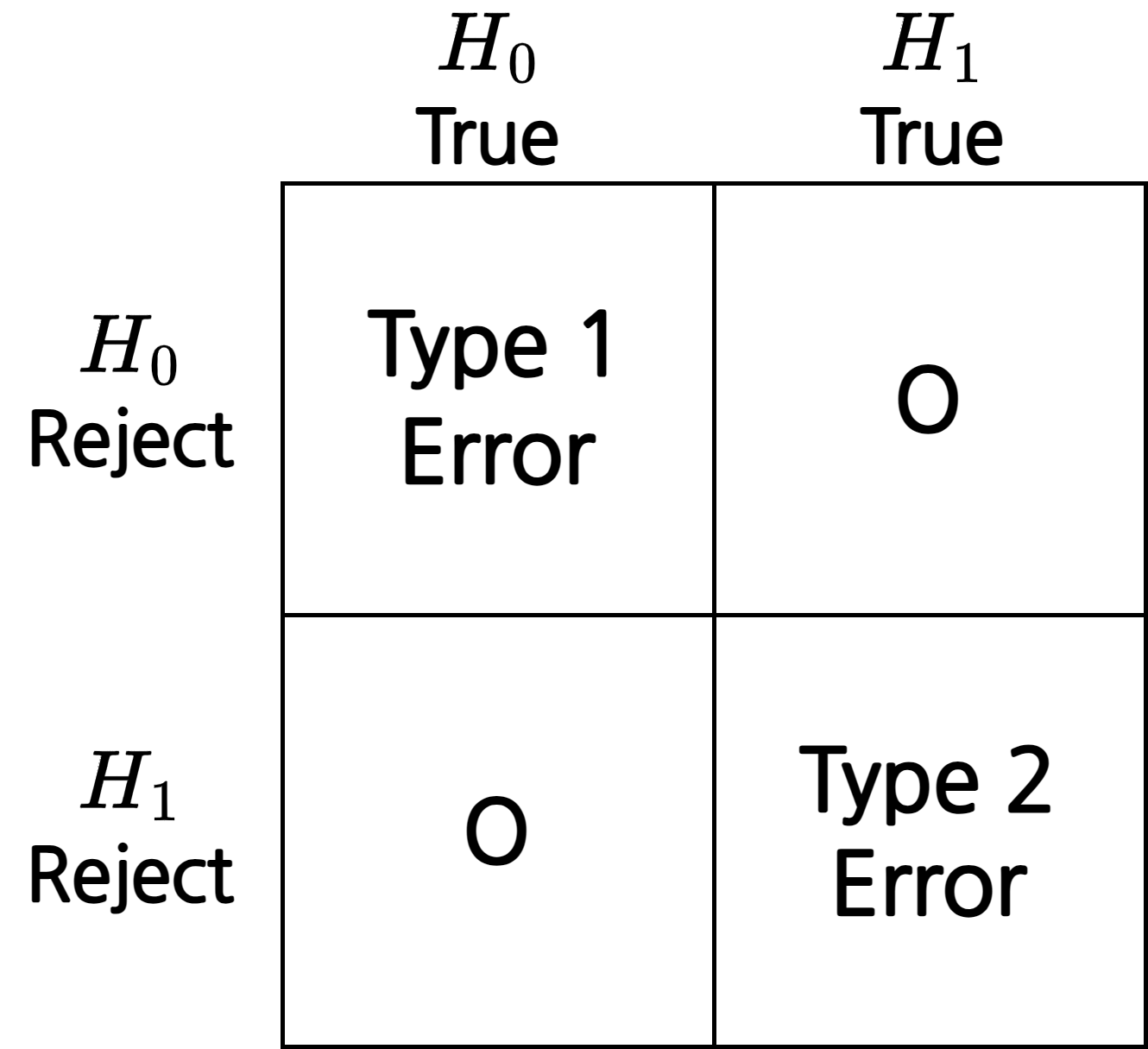
• 결과 표

  

  • 제 1종 오류(Type1 Error): 실제로는 참인데 거짓으로 잘 못 판단
  • 제 2종 오류(Type2 Error): 실제로는 거짓인데 참으로 잘 못 판단
  • 일반적으로 제 1종 오류가 제일 심각한 오류로 여겨짐

평균에 대한 가설 검정

• 모수: \(\mu\)
  1. \(H_0\): \(\mu = a\) vs \(H_1\): \(\mu \lt a\) or \(\mu \gt a\) or \(\mu \neq a\)
  2. \(\bar{x}\), \(\sigma\)(또는 \(s\)), \(n\)을 이용해 \(z\)(\(n \ge 30\)) 또는 \(t\)(\(n \lt 30\)) 계산
  • \(z = \frac{\bar{x}-\mu}{\sigma / \sqrt{n}}\), \(t = \frac{\bar{x}-\mu}{s / \sqrt{n}}\)

모비율에 대한 가설 검정

• 모수: \(p\)
  1. \(H_0\): \(p = p_0\) vs \(H_1\): \(p \lt p_0\) or \(p \gt p_0\) or \(p \neq p_0\)

1. \(\hat{p}\), \(n\)을 이용해 \(z\) 계산

   \[z = \frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1 - p_0)}{n}}}\]

모분산에 대한 가설 검정

• 모수: \(\sigma^2\)
  1. \(H_0\): \(\sigma^2 = a\) vs \(H_1\): \(\sigma^2 \lt a\) or \(\sigma^2 \gt a\) or \(\sigma^2 \neq a\)

1. \(\sigma\), \(s\), \(n\)을 이용해 \(\chi^2\) 계산

   \[\chi^2 = \frac{(n - 1) s^2}{\sigma^2}\]

p-value

• 유의 수준 \(\alpha\): 제 1종 오류가 일어날 확률(넓이)
• p-value: 표본이 귀무가설에 적합한 정도를 0~1 사이의 수치로 표현한 것
  • p-value가 유의수준보다 작다면 귀무가설이 잘못되었다고 판단
• 단측 검정
  • 좌단측
    • p-value: \(P(Z \lt z)\)
    • \(z\) 아래 부분의 확률(넓이)
  • 우단측
    • p-value: \(P(Z \gt z)\)
    • \(z\) 위 부분의 확률(넓이)
• 양측 검정
  • p-value: \(P(Z \lt z) + P(Z \gt z)\)
  • \(-z\) 아래 부분의 확률과 \(z\) 위 부분의 확률의 합
• p-value가 \(\alpha\) 이하라면 \(H_0\)를 기각

두 모수에 대한 가설 검증

\(\sigma^2_1\), \(\sigma^2_2\)가 알려진 경우

1. \(H_0\): \(\mu_1 = \mu_2\) vs \(H_1\): \(\mu_1 \lt \mu_2\) or \(\mu_1 \gt \mu_2\) or \(\mu_1 \neq \mu_2\)

2. \(\bar{x}_1\), \(\bar{x}_2\), \(\sigma^2_1\), \(\sigma^2_2\), \(n_1\), \(n_2\)를 이용해 \(z\) 계산

   \[z = \frac{(\bar{x}_1 - \bar{x}_2) - (0 - 0)}{\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}}\]
   • \(\mu_1 = \mu_2\)이므로 \(0 - 0\)

\(\sigma^2_1\), \(\sigma^2_2\)가 알려지지 않은 경우

1. \(H_0\): \(\mu_1 = \mu_2\) vs \(H_1\): \(\mu_1 \lt \mu_2\) or \(\mu_1 \gt \mu_2\) or \(\mu_1 \neq \mu_2\)

2. \(\bar{x}_1\), \(\bar{x}_2\), \(s^2_1\), \(s^2_2\), \(n_1\), \(n_2\)를 이용해 \(t\) 계산

   • \(\sigma^2_1 = \sigma^2_2\)인 경우

     • 합동 추정량

       \[s^2_p = \frac{(n_1 - 1)s^2_1 + (n_2 - 1)s^2_2}{n_1 + n_2 - 2}\]
     • 자유도: \(df = n_1 + n_2 - 2\)
     • 검정 통계량
     \[t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{s_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}\]
   • \(\sigma^2_1 \neq \sigma^2_2\)인 경우
     • 자유도: \(df = \min(n_1, n_2) - 1\)

     • 검정 통계량

       \[t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}}\]

종속 표본 \(\mu_1 - \mu_2\)

1. \(H_0\): \(\mu_1 = \mu_2\) vs \(H_1\): \(\mu_1 \neq \mu_2\)

2. \(d_i = x_{1i} - x_{2i}\), \(\bar{d} = \frac{1}{n}\sum d_i\), \(s^2_d = \frac{1}{n - 1}\sum (d_i - \bar{d})^2\)

   \[t = \frac{\bar{x} - \mu}{s / \sqrt{n}} = \frac{\bar{d}}{s_d / \sqrt{n}}\]

모비율 차이

• \(\hat{p}_1 = \frac{x_1}{n_1}\), \(\hat{p}_2 = \frac{x_2}{n_2}\)

1. \(H_0\): \(p_1 = p_2\) vs \(H_1\): \(p_1 \lt p_2\) or \(p_1 \gt p_2\) or \(p_1 \neq p_2\)

2. 검정 통계량

   • \(p_1 = p_2\)인 경우

     • $\hat{p} = \frac{x_1 + x_2}{n_1 + n_2}$
     \[z = \frac{\hat{p}_1 - \hat{p}_2}{\sqrt{\hat{p}(1 - \hat{p})(\frac{1}{n_1} + \frac{1}{n_2})}}\]

   • \(p_1 \neq p_2\)인 경우

     \[z = \frac{\hat{p}_1 - \hat{p}_2}{\sqrt{\frac{\hat{p}_1(1 - \hat{p}_1)}{n_1} + \frac{\hat{p}_2(1 - \hat{p}_2)}{n_2}}}\]