강화학습 Chapter 3. 벨만 방정식(Bellman Equation)

참고 자료

이 글은 [노승은, 바닥부터 배우는 강화 학습, 영진닷컴(2020)]을 바탕으로 작성되었습니다.

벨만 방정식(Bellman Equation)

• 주어진 상태의 밸류를 계산하는 방정식
• 재귀적 관계를 이용
  • 시점 \(r\)과 \(r + 1\) 사이의 관계를 이용

1. 벨만 기대 방정식(Bellman Expectation Equation)

0단계

\[\begin{align} & v_\pi(s_t) = \mathbb{E}_\pi[r_{r+1} + \gamma v_\pi(s_{t+1})] \\ & q_\pi(s_t, a_t) = \mathbb{E}_\pi[r_{r+1} + \gamma q_\pi(s_{t+1}, a_{t+1})] \end{align}\]

증명

\[\begin{align} v_\pi(s_t) & = \mathbb{E}_\pi[G_t] \\ & = \mathbb{E}_\pi[r_{t+1}+\gamma r_{r+2} + \gamma^2 r_{r+3} + \cdots] \\ & = \mathbb{E}_\pi[r_{t+1}+\gamma (r_{r+2} + \gamma r_{r+3} + \cdots)] \\ & = \mathbb{E}_\pi[r_{t+1}+\gamma G_{t+1}] \\ & = \mathbb{E}_\pi[r_{t+1}+\gamma v_\pi (s_{t+1})] \end{align}\]

• \(q_\pi(s_t, a_t) = \mathbb{E}_\pi[r_{r+1} + \gamma q_\pi(s_{t+1}, a_{t+1})]\)도 같은 방식으로 증명 가능

퀴즈

1. \(v_\pi(s_t) = r_{r+1} + \gamma v_\pi(s_{t+1})\)가 성립한다
   • 답은 X
   • \(s_t\)에서 \(s_{t+1}\)이 정해지기까지 두 번의 확률 과정을 거쳐야 함
     • 정책이 액션을 선택(\(\pi\)에 의한 선택)
     • 전이 확률이 다음 상태를 선택(\(P_{s_t, s_{t+1}}^{a_{t}}\)에 의한 선택)
   • 다음 시점에 어떤 상태에 도달할 지 모르기 때문에 반드시 기댓값을 사용해야 함
2. \(v_\pi(s_t)= \mathbb{E}_\pi[r_{t+1}+\gamma r_{r+2} + \gamma^2 v_\pi (x_{t+2})]\)
   • 답은 O
   • 재귀적으로 당연함

1단계

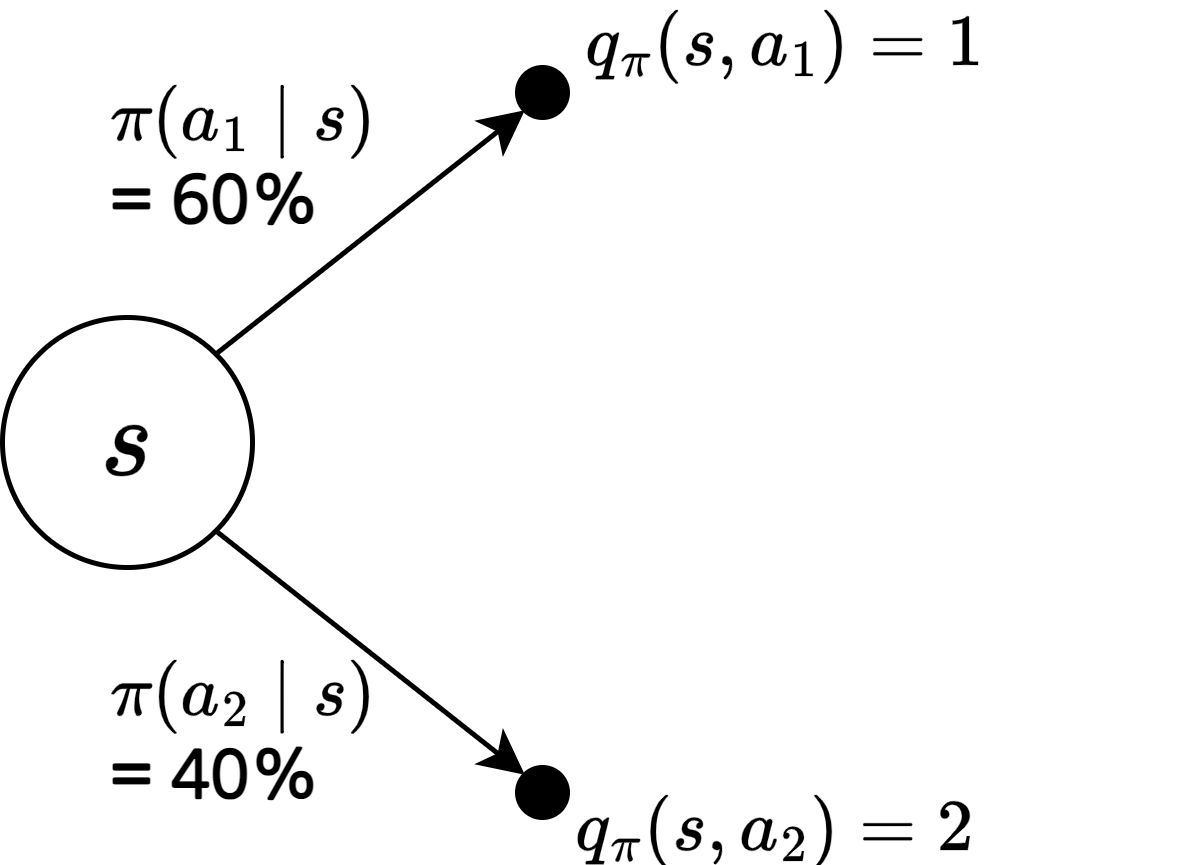
\(q_\pi\)를 이용해 \(v_\pi\) 계산하기

\[v_\pi(s) = \sum_{a\in A} \pi(a\mid s)q_\pi (s, a)\]

• \(s\)에서의 밸류 = (\(s\)에서 \(a\)를 실행할 확률 * \(s\)에서 \(a\)를 실행하는 것의 밸류)들의 합

• 예)

  

\[\begin{align} v_\pi(s) & = \pi(a_1 \mid s) \times q_\pi(s, a_1) + \pi(a_2 \mid s) \times q_\pi(s, a_2) \\ & = 0.6 \times 1 + 0.4 \times 2 \\ & = 1.4 \end{align}\]

\(v_\pi\)를 이용해 \(q_\pi\) 계산하기

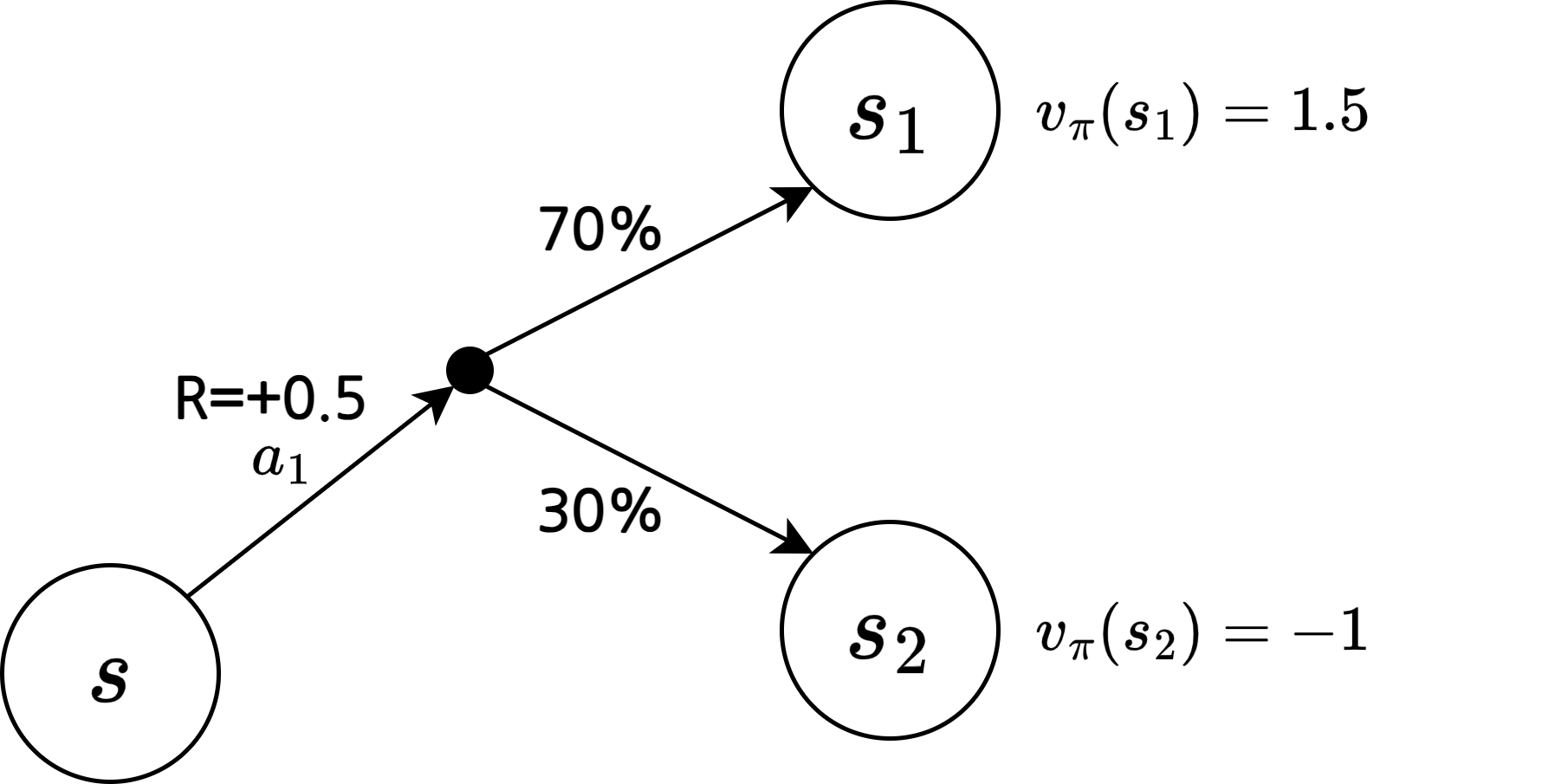
\[q_\pi(s, a) = r_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a v_\pi (s^\prime)\]

• \(s\)에서 \(a\)를 실행하는 것의 밸류 = \(s\)에서 \(a\)를 실행할 때의 보상(즉시 얻는 보상) + 감쇠 인자 * (\(s\)에서 \(a\)를 실행하면 \(s^\prime\)에 도착할 확률 * \(s^\prime\)의 밸류)들의 합

• 예)

  

\[\begin{align} q_\pi (s, a_1) & = r_s^{a_1} + P_{ss_1}^a \times v_\pi(s_1) + P_{ss_2}^a \times v_\pi(s_2) \\ & = 0.5 + 0.7 \times 1.5 + 0.3 \times (-1) \\ & = 1.25 \end{align}\]

2단계

\[\begin{align} & v_\pi(s) = \sum_{a\in A} \pi(a\mid s)q_\pi (s, a) = \sum_{a\in A} \pi(a\mid s) \left( r_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a v_\pi (s^\prime) \right) \quad \because q_\pi(s, a) = r_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a v_\pi (s^\prime) \\ & q_\pi(s, a) = r_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a v_\pi (s^\prime) = r_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a \sum_{a^\prime\in A} \pi(a^\prime \mid s^\prime)q_\pi (s^\prime, a^\prime) \quad \because v_\pi(s^\prime) = \sum_{a^\prime\in A} \pi(a^\prime \mid s^\prime)q_\pi (s^\prime, a^\prime) \end{align}\]

• 1단계에서 구한 \(q_\pi(s, a)\)와 \(v_\pi(s)\)를 대입

0단계와의 비교

• 0단계: \(v_\pi(s_t) = \mathbb{E}_\pi[r_{r+1} + \gamma v_\pi(s_{t+1})]\)
• 2단계: \(v_\pi(s) = \sum_{a\in A} \pi(a\mid s) \left( r_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a v_\pi (s^\prime) \right)\)
  • 2단계는 0단계의 기댓값 연산자를 확률과 밸류의 곱 형태로 풀어서 쓴 형태
• 2단계를 계산하기 위해서는 \(r_s^a\)와 \(P_{ss^\prime}^a\)를 반드시 알아야 함
  • 하지만 \(r_s^a\)와 \(P_{ss^\prime}^a\)는 환경의 일부
    • \(r_s^a\)를 미리 알고 있다는 것은 \(s\)에서 \(a\)를 했을 때 얼마의 보상을 받을지 기댓값을 안다는 뜻
    • \(P_{ss^\prime}^a\)를 미리 알고 있다는 것은 \(s\)에서 \(a\)를 했을 때 어떤 상태에 도달할지 확률 분포를 알고 있다는 뜻
    • 하지만 \(s\)에서 \(a\)를 해보기도 전에 미리 \(r_s^a\)와 \(P_{ss^\prime}^a\)를 아는 것은 매우 어려움
  • \(r_s^a\)와 \(P_{ss^\prime}^a\)를 알 때 “MDP를 안다”고 표현
• 모델-프리(model-free) 접근법: MDP를 모를 때 경험하며 학습하는 접근법
• 모델-기반(model-based) 접근법 또는 플래닝(planning): MDP를 알 때 학습하는 접근법

2. 벨만 최적 방정식(Bellman Optimality Equation)

최적 밸류와 최적 상태

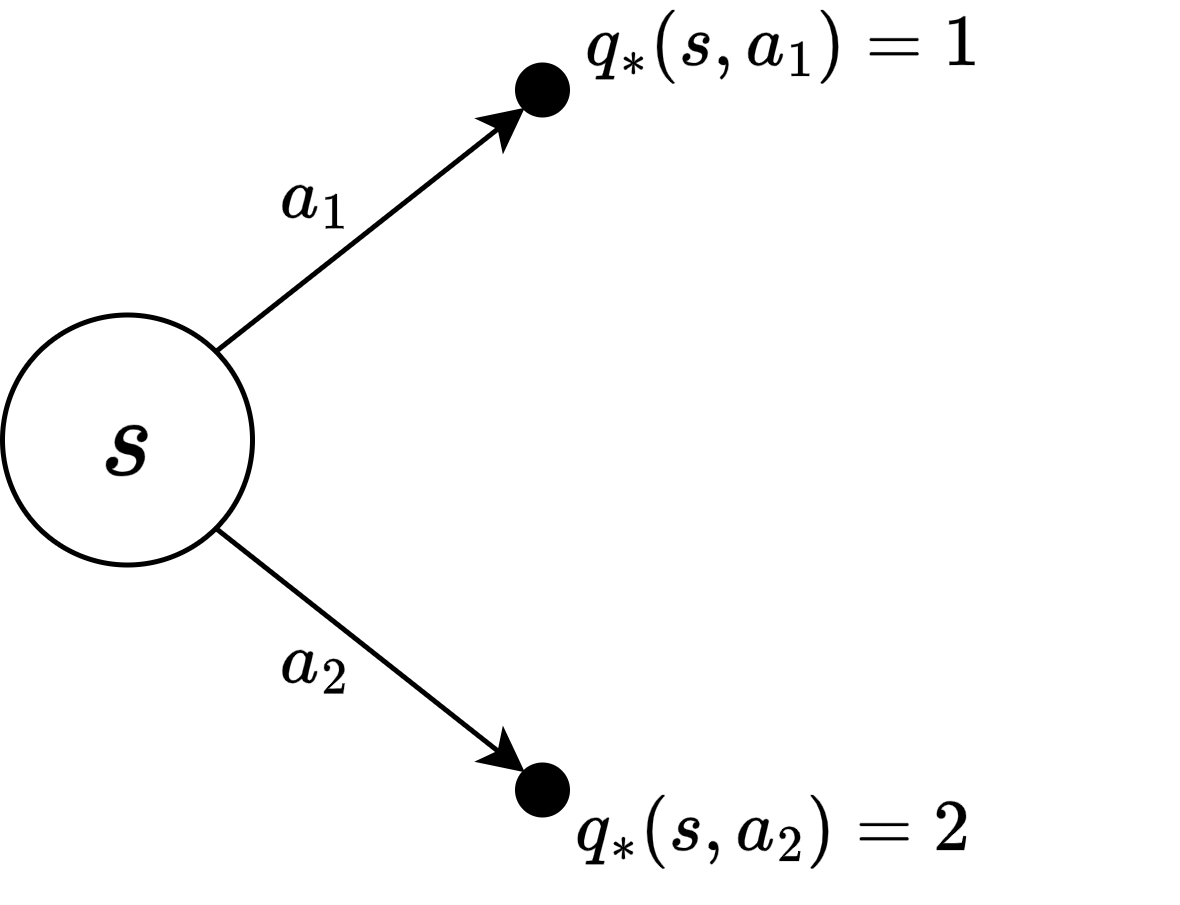
최적 밸류(optimal value)

\[\begin{align} & v_*(s) = \max_\pi v_\pi (s) \\ & q_*(s, a) = \max_\pi q_\pi (s, a) \end{align}\]

• MDP 안에 존재하는 모든 \(\pi\) 중 가장 좋은 \(\pi\)를 선택하여 계산한 밸류
  • \(v_* (s)\): \(v_\pi (s)\)의 값을 가장 높게 하는 \(\pi\)를 선택하여 계산
  • \(q_* (s, a)\): \(q_\pi (s, a)\)의 값을 가장 높게 하는 \(\pi\)를 선택하여 계산
• 예)
  • 가능한 정책의 집합 \(\{\pi_1, \pi_2, \pi_3, ...\}\)
  • 상태 \(s_0\)에서의 밸류의 집합 \(\{v_{\pi_1}(s_0),v_{\pi_2}(s_0),v_{\pi_3}(s_0), ...\}\)
    • 밸류의 집합에서 가장 큰 값이 \(v_{\pi_5}(s_0)\)라면 \(v_*(s_0) = v_{\pi_5}(s_0)\)
  • 만약 상태별로 가장 높은 밸류를 주는 정책이 모두 다르다면?
    • \(s_0\)에서는 \(\pi_5\)를 따를 때 최고지만, \(s_1\)에서는 \(\pi_3\)를 따를 때 최고라면?

    • \(s_0\)에서는 \(\pi_5\)를 따르고, \(s_1\)에서는 \(\pi_3\)를 따르는 새로운 정책 \(\pi_*\)를 만들면 됨

      여기서 \(\pi_*\)를 최적 정책이라고 부름

최적 정책(optimal policy)

• 모든 상태 \(s\)에 대해, \(v_{\pi_1}(s) \gt v_{\pi_2}(s)\)이면 \(\pi_1 \gt \pi_2\)
  • 부분 순서(partial ordering): 모든 정책 중 일부만 비교해여 순서를 정할 수 있다는 뜻
    • 모든 정책 사이의 서열을 매기는 것을 불가능(\(s_0\)에서는 \(\pi_5\)가 최고지만, \(s_1\)에서는 \(\pi_3\)이 최고일 수 있음)

    • 따라서 서열을 매길 수 있는 정책들이 부분적으로 존재

      MDP 내의 모든 \(\pi\)에 대해 \(\pi_* \gt \pi\)를 만족하는 \(\pi_*\)가 반드시 존재한다.

• 최적 정책: \(\pi_*\)
• 최적 밸류: \(v_*(s) = v_{\pi_*}(s)\)
• 최적 액션 밸류: \(q_*(s, a) = q_{\pi_*}(s, a)\)

0단계

\[\begin{align} & v_*(s) = \max_a \mathbb{E} \left[r + \gamma v_*(s^\prime) \mid s_t = s, a_t = a\right] \\ & q_*(s, a) = \mathbb{E} \left[r + \gamma \max_{a^\prime}q_*(s^\prime, a^\prime) \mid s_t = s, a_t = a\right] \end{align}\]

• 벨만 기대 방정식과 비교하면 \(\mathbb {E}_\pi\) 대신 \(\mathbb{E}\) 사용
  • 벨만 기대 방정식에서는 주어진 \(\pi\)가 액션을 선택
  • 벨만 최적 방정식에서는 모든 액션들 중 기댓값을 가장 크게하는 \(a\)를 선택
  • 따라서 \(\pi\)의 역할이 없어짐

1단계

\(q_*\)를 이용해 \(v_*\) 계산하기

\[v_*(s) = \max_a q_*(s, a)\]

• \(s\)의 최적 밸류 = \(s\)에서 선택할 수 있는 \(a\) 중 액션 밸류가 가장 높아지는 \(a\)

• 예)

  

\[\begin{align} v_*(s) & = \max_a q_*(s, a) \\ & = \max(q_*(s, a_1), q_*(s, a_2)) \\ & = \max(1, 2) = 2 \end{align}\]

\(v_*\)를 이용해 \(q_*\) 계산하기

\[q_*(s, a) = r_s^a + \gamma \sum_{s^\prime \in S} p_{ss^\prime}^a v_*(s^\prime)\]

2단계

\[\begin{align} & v_*(s) = \max_a q_*(s, a) = \max_a \left[ r_s^a + \gamma \sum_{s^\prime \in S} p_{ss^\prime}^a v_*(s^\prime) \right] \quad \because q_*(s, a) = r_s^a + \gamma \sum_{s^\prime \in S} p_{ss^\prime}^a v_*(s^\prime) \\ & q_*(s, a) = r_s^a + \gamma \sum_{s^\prime \in S} p_{ss^\prime}^a v_*(s^\prime) = r_s^a + \gamma \sum_{s^\prime \in S} p_{ss^\prime}^a \max_{a^\prime} q_*(s^\prime, a^\prime) \quad \because v_*(s^\prime) = \max_{a^\prime} q_*(s^\prime, a^\prime) \end{align}\]

• 정책 \(\pi\)가 주여져 있고, \(\pi\)를 평가하고 싶을 때에는 벨만 기대 방정식 사용
• 최적의 밸류를 찾고 싶을 때는 벨만 최적 방정식 사용