강화학습 Chapter 4. MDP를 알 때의 플래닝

참고 자료

이 글은 [노승은, 바닥부터 배우는 강화 학습, 영진닷컴(2020)]을 바탕으로 작성되었습니다.

MDP를 알 때의 플래닝

• 이번 챕터에서 다룰 내용의 전제 조건
  1. 작은 문제
     • 상태 집합 \(S\)나 액션 집합 \(A\)의 크기가 작은 경우
  2. MDP를 알고 있음
     • 보상 함수와 전이 확률 행렬을 알고 있음
• 플래닝(planning): MDP에 대한 모든 정보를 알 때 이를 이용하여 정책을 개선하는 과정
• 테이블 기반 방법론(tabular method)
  • 모든 상태 \(s\)나 상태와 액션의 페어 \((s, a)\)에 대한 테이블을 생성
  • 테이블의 값을 업데이트하며 반복
  • 작은 문제일 때 주로 사용

1. 밸류 평가하기 - 반복적 정책 평가

• 반복적 정책 평가(Iterative policy evaluation)
  1. 테이블의 값 초기화
  2. 벨만 기대 방정식을 이용해 테이블의 값을 조금씩 업데이트

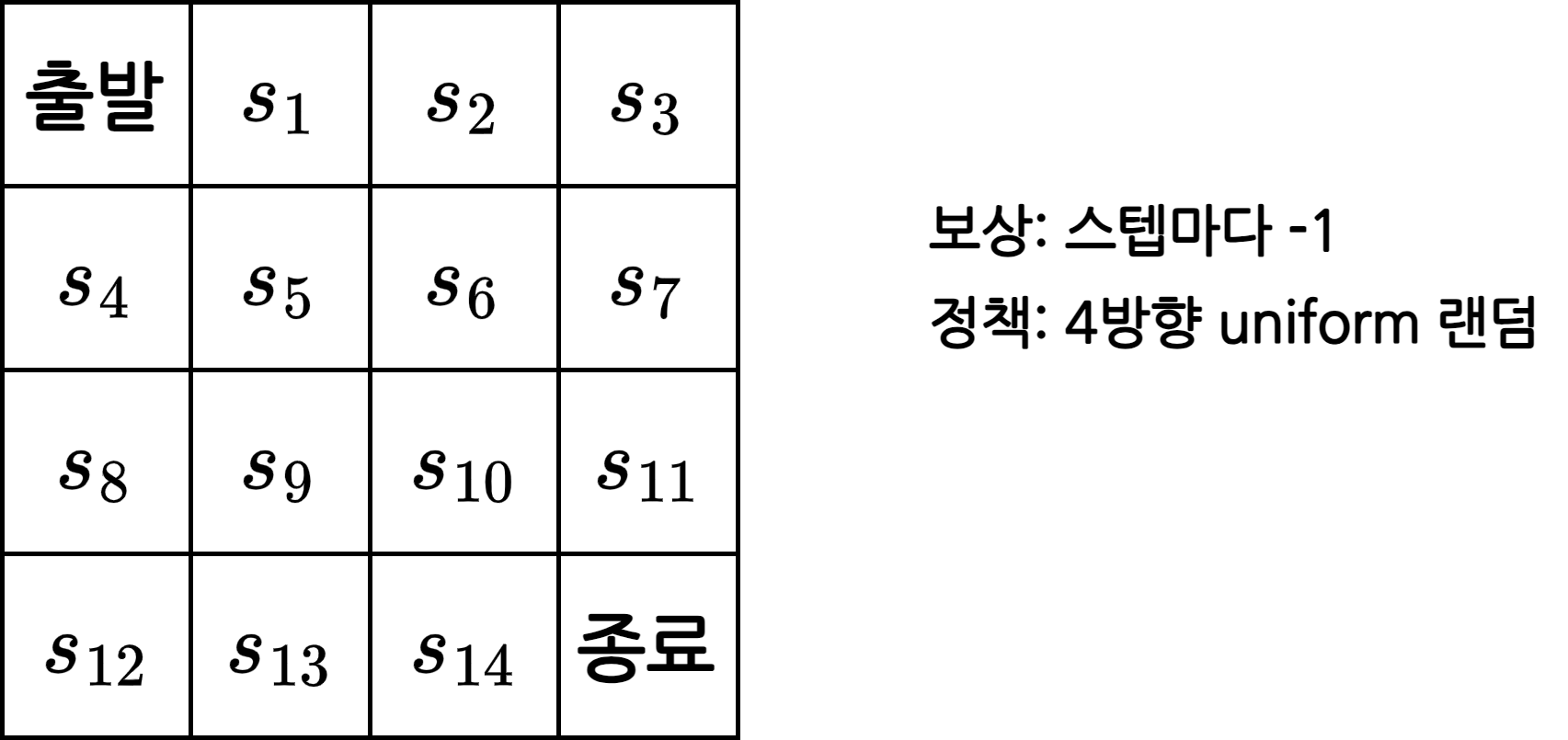
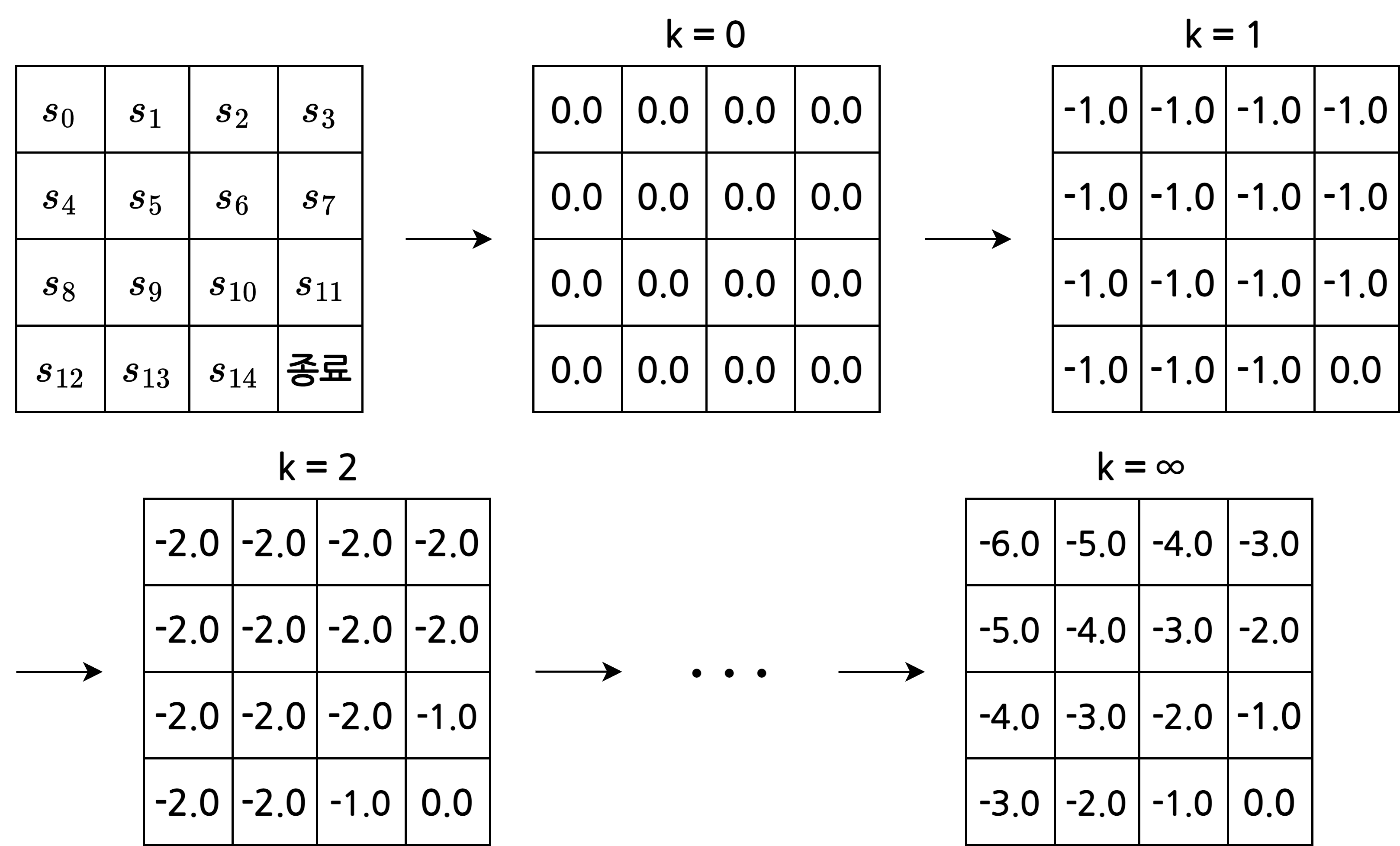
그리드 월드 예시

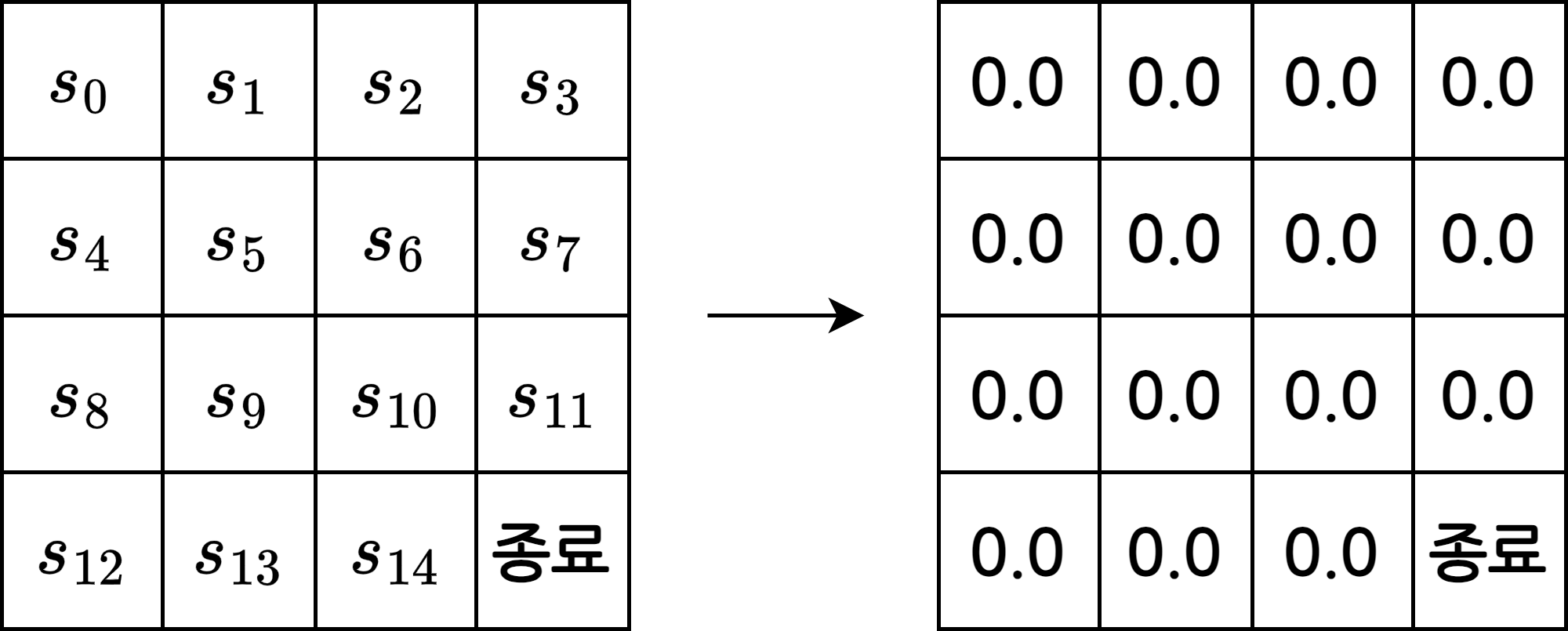
1. 테이블 초기화

• 테이블에 상태별 밸류 \(v(s)\)를 기록하기 때문에 상태 \(s\)의 개수만큼의 빈칸이 필요
  • 이번 예시에서는 상태가 16개
• 어떤 값으로 초기화 해도 상관 없음
  • 적당한 값인 0으로 초기화

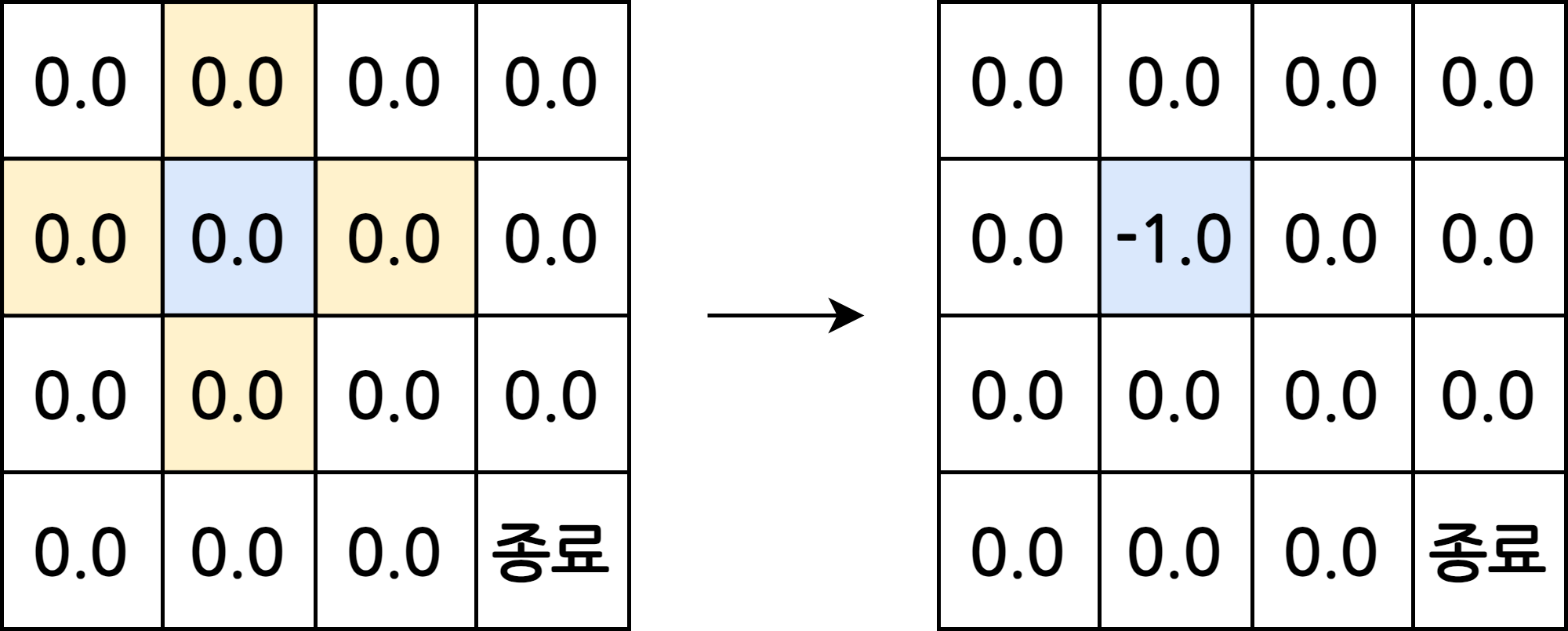
2. 상태의 값을 업데이트

• \(s_5\)의 다음 상태가 될 후보는 동서남북 4칸(\(s_1\), \(s_4\), \(s_6\), \(s_9\))

• \(r_s^a\)와 \(P_{ss^\prime}^a\)를 알기 때문에 벨만 기대 방정식을 사용하여 밸류를 구할 수 있음

  \[v_\pi(s) = \sum_{a\in A} \pi(a\mid s) \left( r_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a v_\pi (s^\prime) \right)\]
  • 4방향 랜덤이므로 \(\pi(a \mid s)\)는 0.25
  • 보상 \(r_s^a\)는 -1
  • \(\gamma\)는 1로 계산

  • \(\pi(a \mid s)\)를 통해 동서남북 중 어느 방향으로 이동할지 액션을 정하고 실행하면 무조건 해당 상태에 도착하므로 \(P_{ss^\prime}^a\)는 1

    \[\begin{align} v_{pi}(s_5) = \; & 0.25 \times(-1 + 1 \times (1 \times 0.0)) + 0.25 \times(-1 + 1 \times (1 \times 0.0)) \\ & + 0.25 \times(-1 + 1 \times (1 \times 0.0)) + 0.25 \times(-1 + 1 \times (1 \times 0.0)) = -1.0 \end{align}\]

• 종료 상태를 제외한 모든 상태에 대해 밸류를 계산
  • 업데이트 할 때는 새로 업데이트 된 밸류가 아닌 업데이트 이전의 값을 사용
    • \(s_5\)를 업데이트하고 \(s_6\)를 업데이트 할 때, 업데이트 된 \(s_5\)의 밸류인 -1.0이 아닌 이전 \(s_5\)의 밸류인 0.0을 사용
  • 종료 상태의 밸류는 0

3. 과정 2를 반복

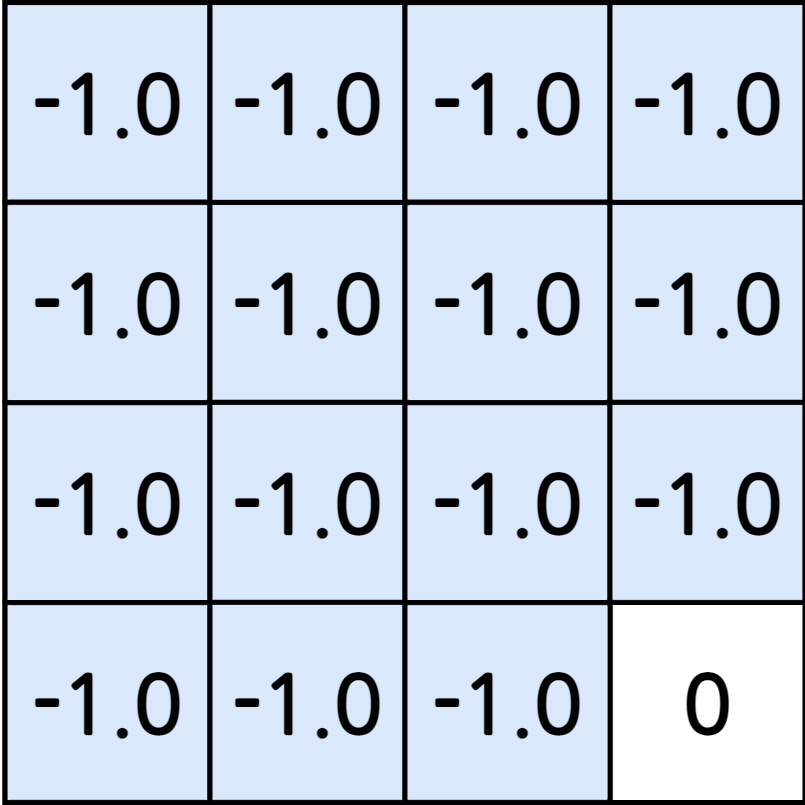
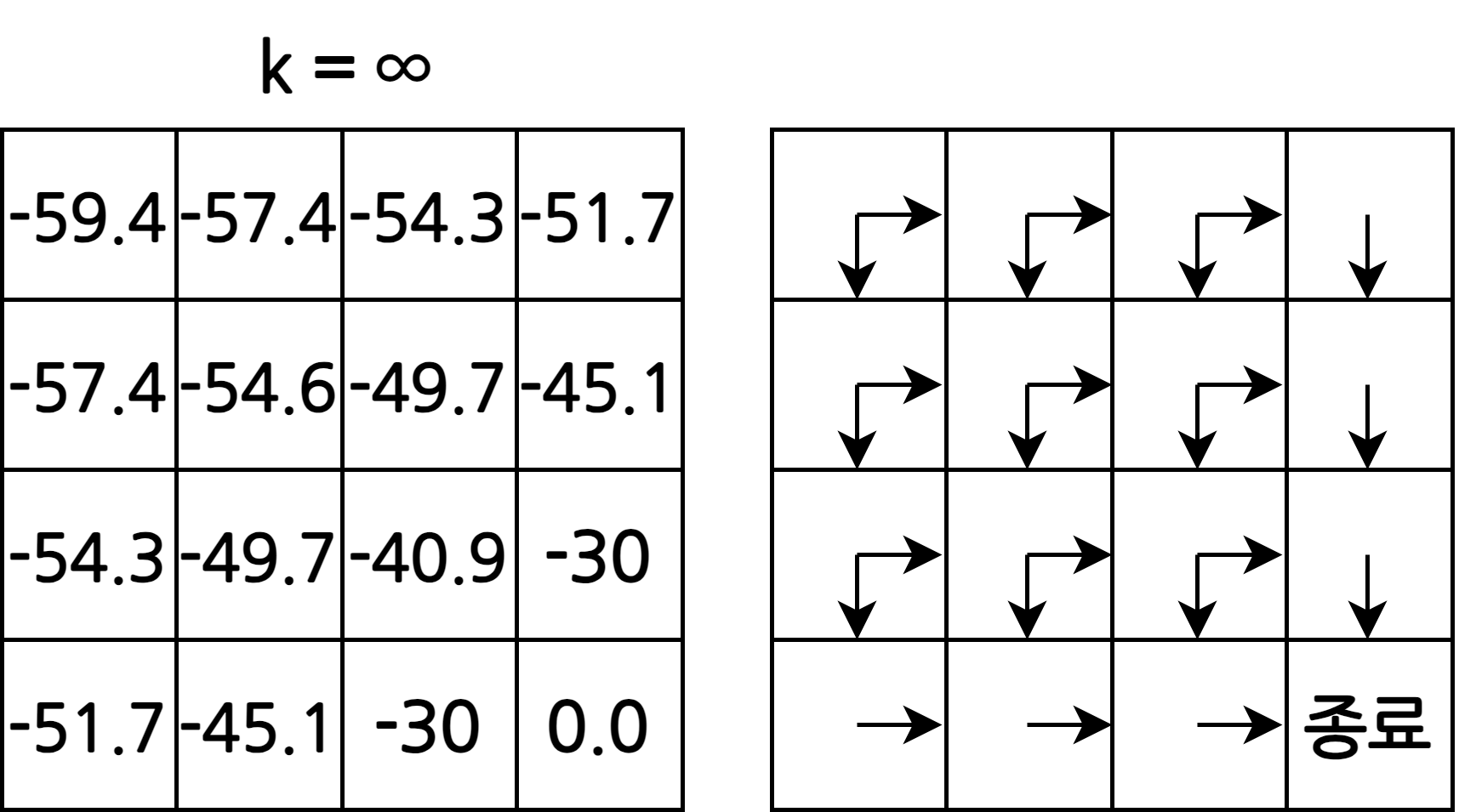
• 계속 반복하면 어떤 값에 수렴

  항상 수렴하는 이유 참고

• 반복된 업데이트를 통해 각 상태의 실제 가치를 알 수 있음
  • \(s_0\)의 밸류는 -59.4로 무작위로 움직일 때 대락 60번 움직여야 종료 상태에 도착한다는 의미

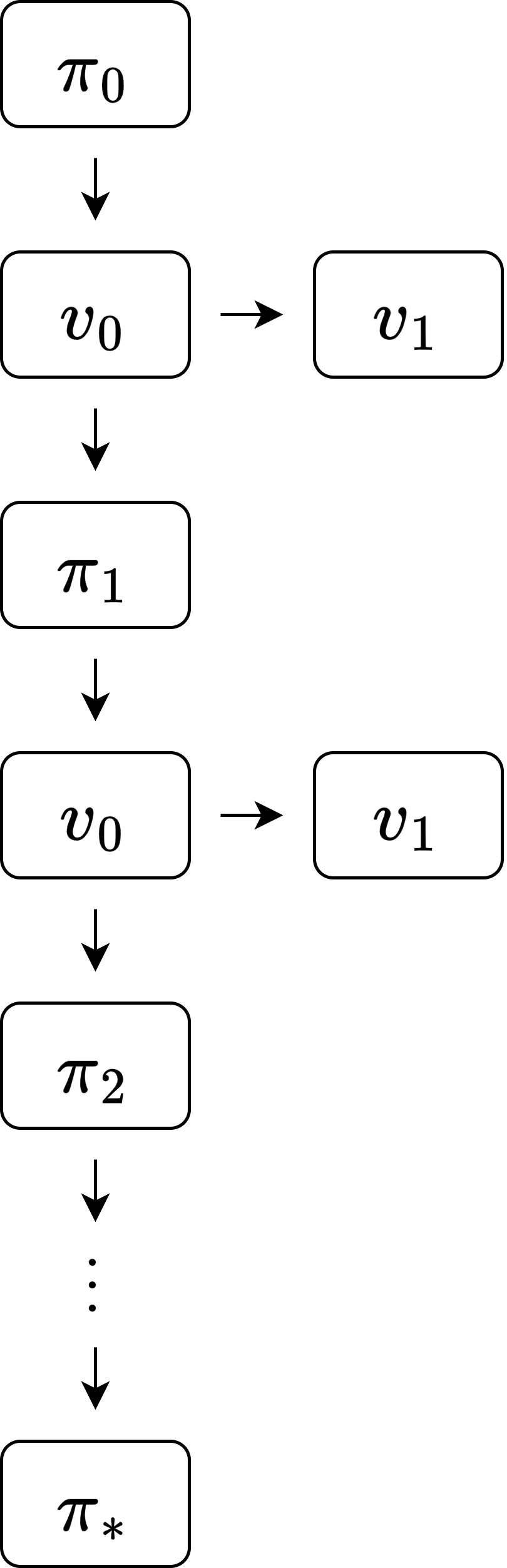
2. 최고의 정책 찾기 - 정책 이터레이션

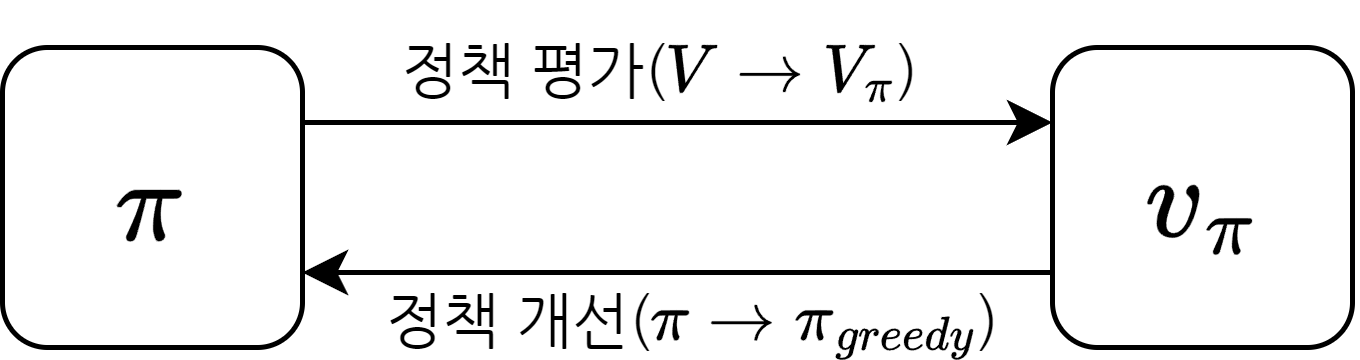
평가와 개선의 반복

정책 평가(policy evaluation)

• 고정된 \(\pi\)에 대한 각 상태의 밸류 계산
• 반복적 정책 평가 사용

정책 개선(policy improvement)

• 새로운 정책 \(\pi^\prime\) 생성
• 정책 평가에서 구한 \(v(s)\)에 대한 그리디 정책을 생성

• 정책 평가와 정책 개선을 계속 반복하다보면 정책과 그에 따른 가치 모두 변하지 않는 단계에 도달
  • 도달한 곳의 정책과 가치가 바로 최적 정책과 최적 가치

그리드 월드 예시

• \(s_5\)에서 가치를 높일 수 있는 액션은 \(a_남\)과 \(a_동\)
  • 따라서 \(\pi^\prime (a_동 \mid s_5) = 1.0 \; or \; \pi^\prime (a_남 \mid s_5) = 1.0\)과 같은 정책을 생각해 볼 수 있음
  • 이렇게 눈 앞의 이익을 최대화 하는 선택을 하는 정책을 그리디 정책(greedy policy)이라고 함
• 각 상태에 대해 그리디 정책을 계산하면 더 좋은 정책을 얻을 수 있음

예시에서는 한 번만 그리디 정책을 계산해 최적 정책을 얻었지만 실제로 이런 경우는 별로 없음

정책이 반드시 개선되는 이유

• \(\pi_{greedy}\): 딱 한 칸(\(s\))만 그리디 정책으로 움직이고 나머지는 원래 정책 \(\pi\)을 따르는 정책
  • 반드시 \(\pi_{greedy} \gt \pi\)
• 귀납적으로 적용하면 \(s\) 다음 칸에서도 그리디하게 움직이는게 좋고, 또 다음 칸에서도 좋음
• 따라서 모든 상태에서 그리디한 정책이 원래 정책보다 좋음

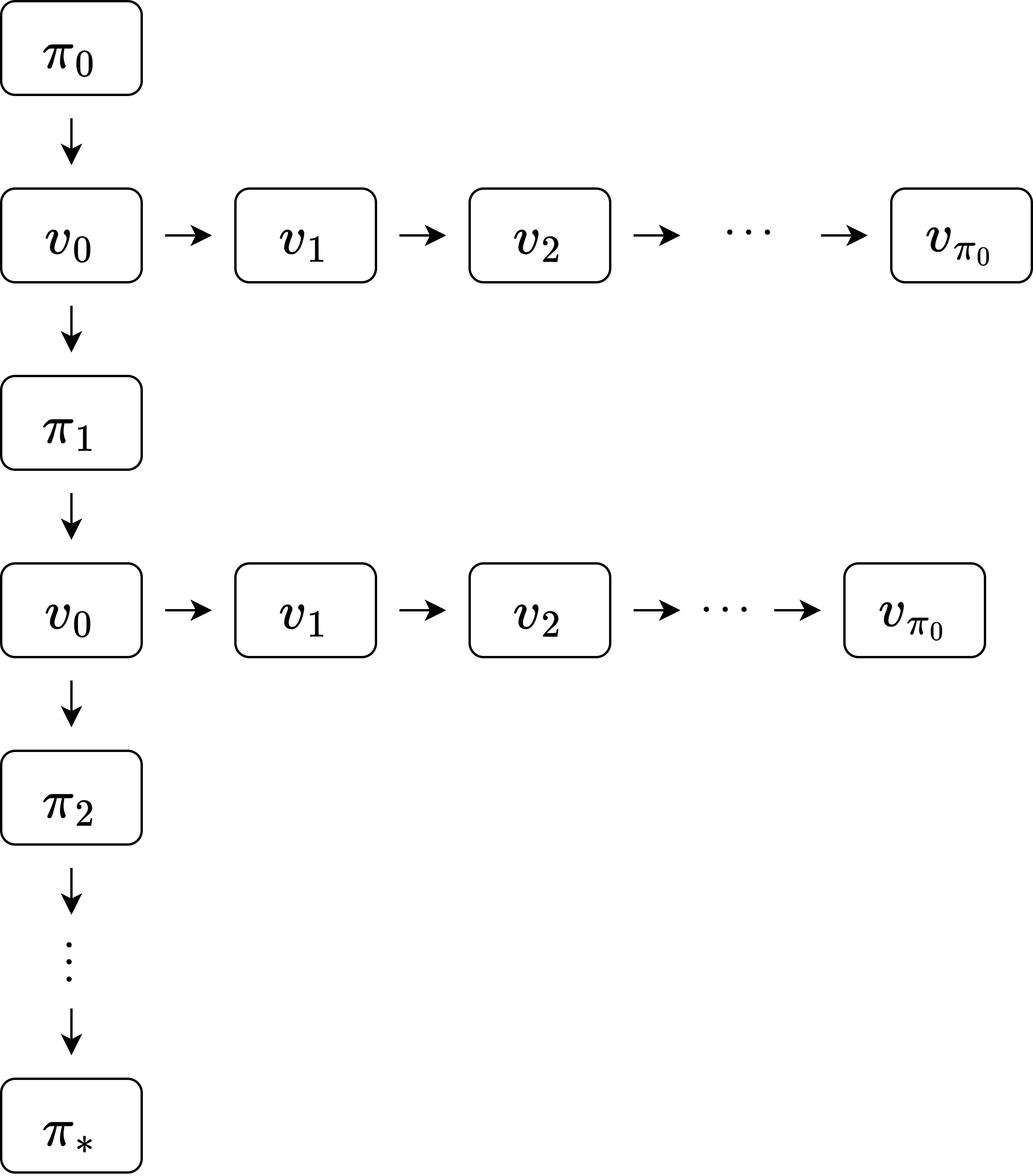
정책 평가 간소화

• 세로로 이어지는 루프(정책 이터레이션) 안에 가로로 이어지는 루프(정책 평가)가 포함되어 있음
  • 따라서 복잡하고 느릴 수도 있음

• 반복적 정책 평가를 수렴할 때까지 하지 않고 일찍 멈춰(early stopping)도 최적 정책을 구할 수 있음
  • 가치 평가를 수렴할 때까지 하지 않아도 된다는 것을 알 수 있음

• 이렇게 하면 간결하고 빠르게 최적 정책을 찾을 수 있음

최고의 정책 찾기 - 밸류 이터레이션

• 벨만 최적 방정식을 이용해 단번에 최적 정책을 도출

1. 테이블 초기화

• 정책 이터레이션에서는 테이블의 값이 \(\pi\)의 밸류였다면 밸류 이터레이션에서는 최적 정책 \(\pi^*\)의 밸류인 \(v_*(s)\)를 의미

2. 값 업데이트

• 벨만 최적 방정식을 이용하여 값을 업데이트

  \[v_*(s) = \max_a \left[ r_s^a + \gamma \sum_{s^\prime \in S} p_{ss^\prime}^a v_*(s^\prime) \right]\]
  • 가능한 \(a\) 중 가장 밸류가 큰 액션의 값을 선택
  • 보상 \(r_s^a\)는 -1
  • \(\gamma\)는 1로 계산
  • 동서남북 중 하나의 방향으로 이동하는 액션을 실행하면 무조건 해당 상태에 도착하므로 \(P_{ss^\prime}^a\)는 1
  • \[v_*(s_5) = \max(-1 + 1.0 \times (1 \times 0.0), -1 + 1.0 \times (1 \times 0.0), -1 + 1.0 \times (1 \times 0.0), -1 + 1.0 \times (1 \times 0.0)) = -1.0\]

• 모든 상태에 대해 벨만 최적 방정식을 적용해 값을 업데이트

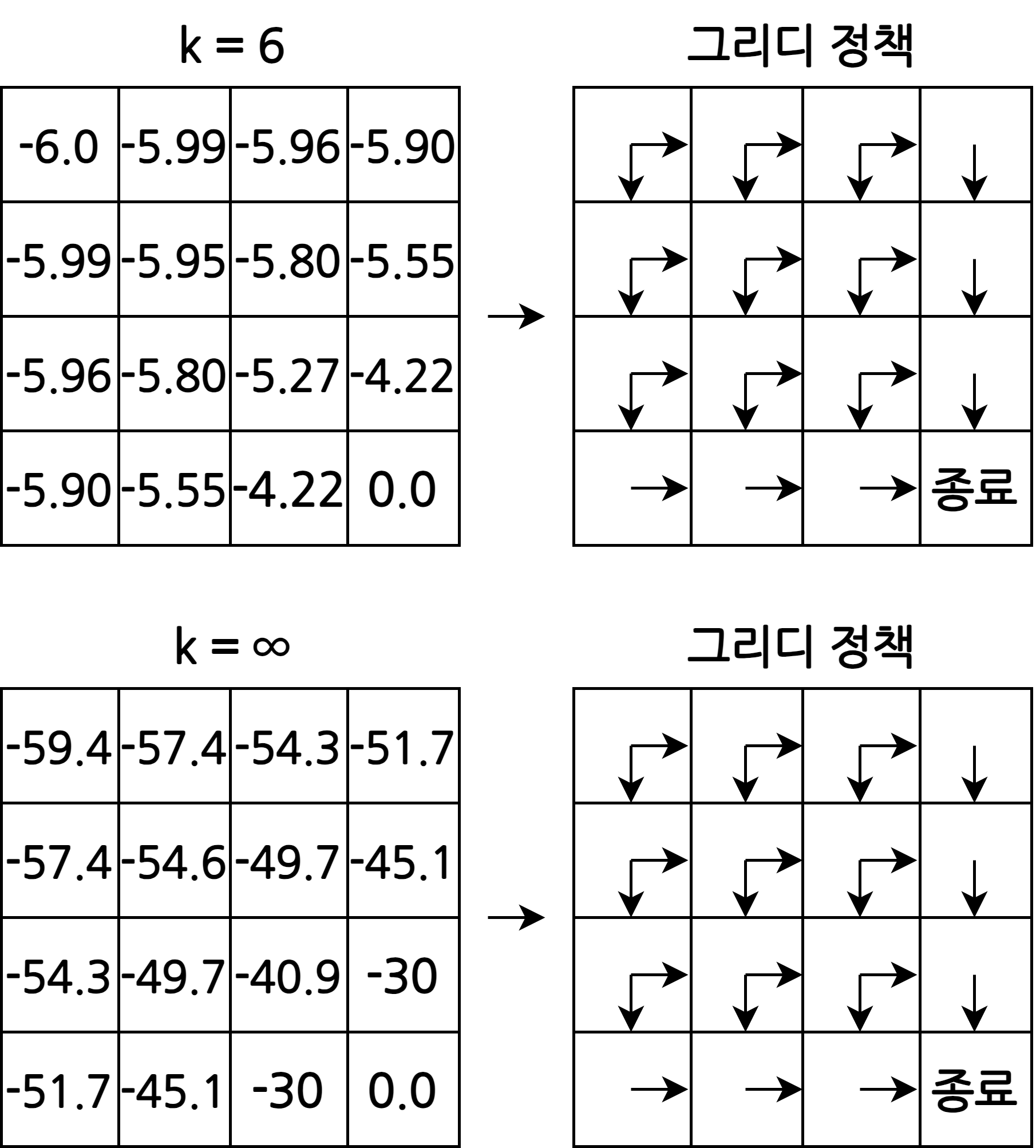
3. 과정 2를 반복

• 수렴할 때까지 과정 2를 충분히 반복

4. 최적 정책 도출

• 과정 3에서 구한 결과에 대한 그리디 정책을 생성