강화학습 Chapter 5. MDP를 모를 때 밸류 평가하기

참고 자료

이 글은 [노승은, 바닥부터 배우는 강화 학습, 영진닷컴(2020)]을 바탕으로 작성되었습니다.

MDP를 모를 때 밸류 평가하기

• 이번 챕터에서 다룰 내용의 전제 조건
  1. 작은 문제
  2. MDP를 모름
• 모델 프리 상황에서의 prediction 방법에 대해 다룸
  • \(\pi\)가 주어졌을 때 가치를 평가하는 방법

1. 몬테카를로 학습

몬테카를로 방법론(Monte Carlo Method)

• 반복적인 샘플링을 통해 근사적으로 값을 가늠하는 방법

• 예)
  • 동전을 던져 앞면과 뒷면이 나올 확률 구하기
    • 10번 던져 앞면이 3번 나왔다면 앞면이 나올 확률은 0.3
    • 100번 던져 앞면이 35번 나왔다면 앞면이 나올 확률은 0.35
    • 더 많이 던질 수록 값이 정확해질 가능성이 큼
• 밸류를 구하기 위해 여러번의 에피소드를 경험시킨 후 얻은 리턴의 평균을 통해 리턴의 기댓값을 구할 수 있음

  • 마찬가지로 샘플이 많을 수록, 즉 여러번의 에피소드를 경험할 수록 밸류의 예측치는 정확해짐

    \(v_\pi(s_t) = \mathbb{E}_\pi[G_t]\) 가치 함수는 리턴의 기댓값

몬테카를로 학습 알고리즘

• MDP를 모르는 상태라 가정

  • \(r_s^a\)와 \(P_{ss^\prime}^a\)를 모름

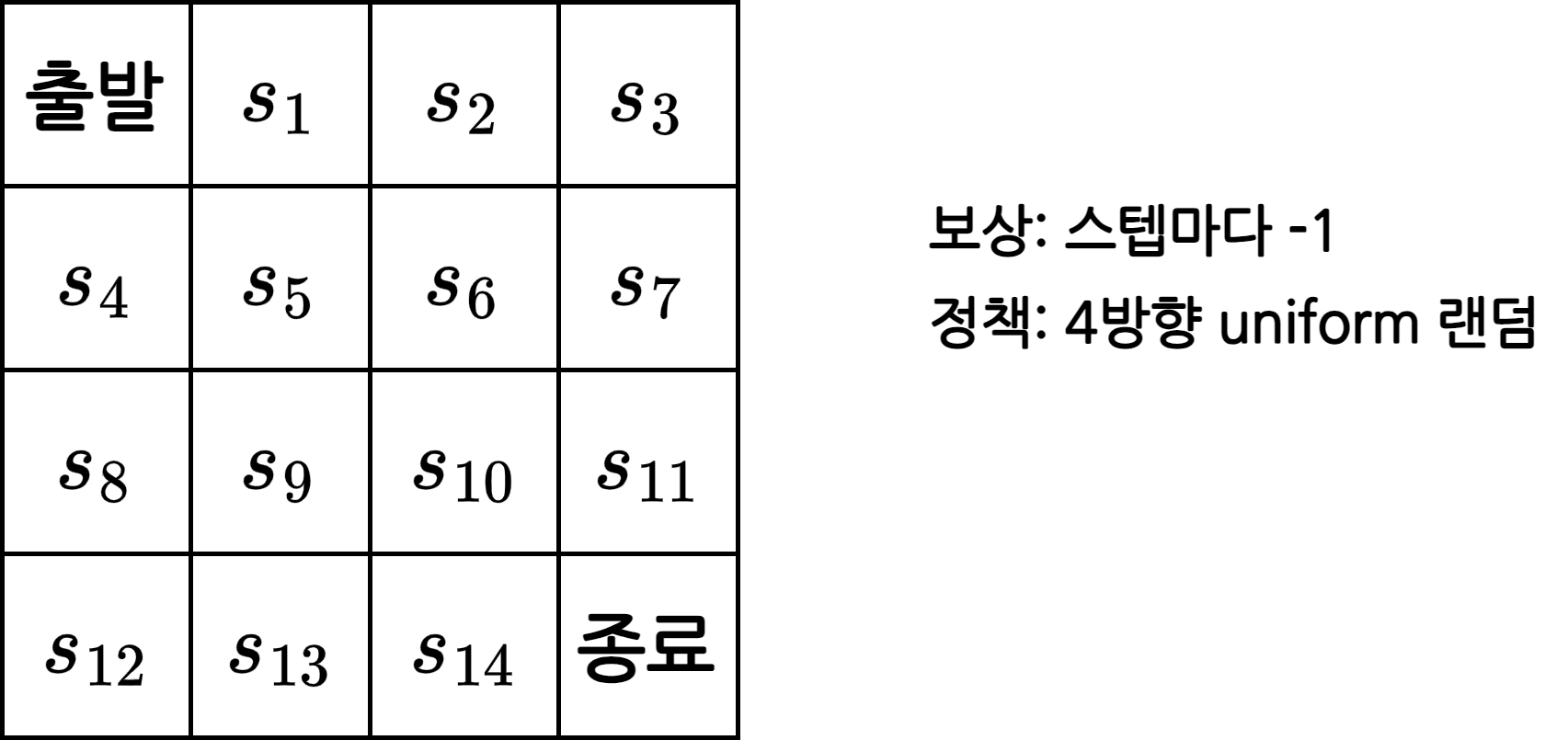
    \(r_s^a\)와 \(P_{ss^\prime}^a\)를 모르는 것일 뿐 MDP에는 고정된 \(r_s^a\)와 \(P_{ss^\prime}^a\)가 있음

    이전과 마찬가지로 \(r_s^a\)는 스텝마다 -1이며, \(P_{ss^\prime}^a\)도 1로 동일함

• 현재 에이전트는 액션을 선택했을 때, 어떤 상태에 도달할지 모르는 상황

  • 따라서 여러번의 경험을 통해 보상과 전이 함수를 예측해야 함

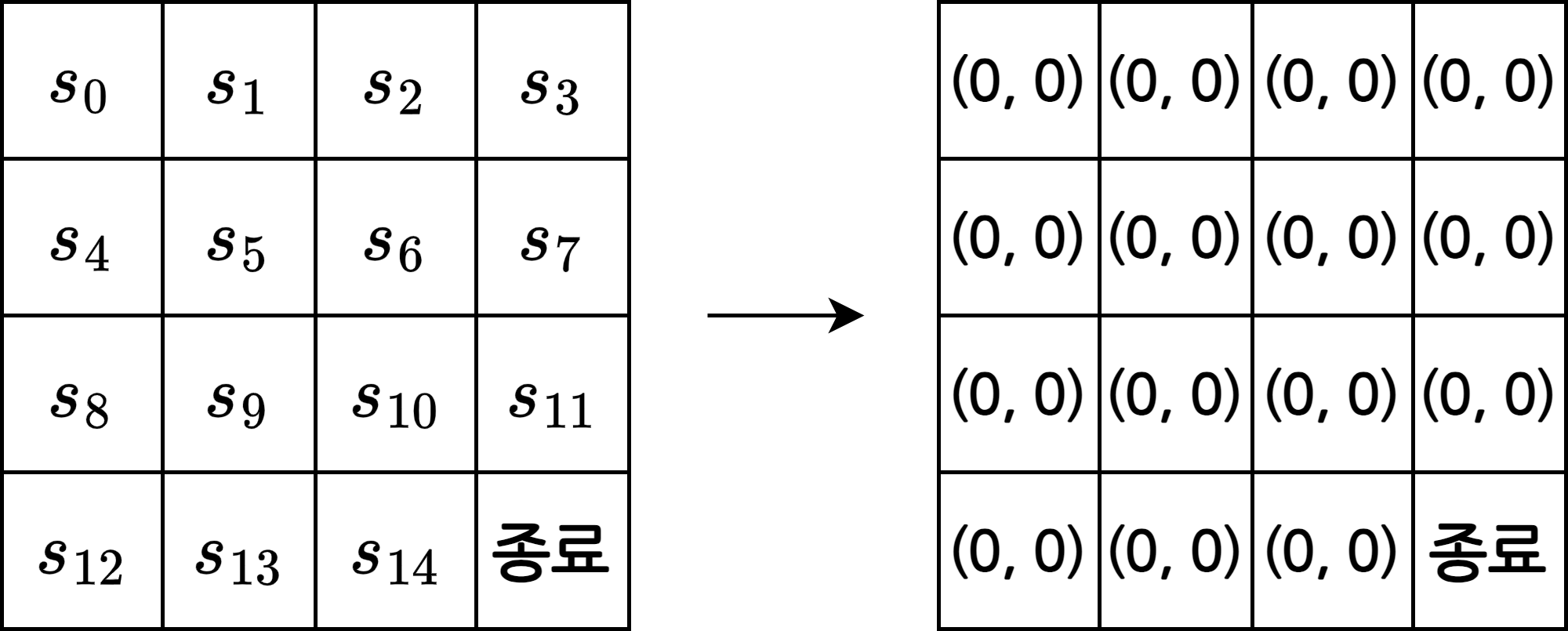
1. 테이블 초기화

• 상태별로 \(N(s)\)와 \(V(s)\) 값 0으로 초기화
  • \(N(s)\): \(s\)를 방문한 횟수
  • \(V(s)\): \(s\)에서 경험한 리턴의 총합

2. 경험 쌓기

• 평가하고 싶은 정책 \(\pi\)를 따르는 에이전트가 한 번의 에피소드를 경험

\[s_0, a_0, r_0, s_1, a_1, r_1, s_2, a_2, r_2,..., s_{T-1}, a_{T-1}, r_{T-1}, s_T\]

• 한 번의 에피소드를 위와 같이 표현할 수 있음
  • 여기서 \(s_0\), \(s_1\), \(s_2\)는 시점 0, 1, 2에서의 상태를 뜻함

\[\displaylines { G_0 = r_0 + \gamma r_1 + \gamma^2 r_2 + \gamma^3 r_3 + \cdots + \gamma^{T-1}r_{T-1} \\ G_1 = r_1 + \gamma r_2 + \gamma^2 r_3 + \cdots + \gamma^{T-2}r_{T-2} \\ \cdots \\ G_{T-1} = r_1 \\ G_T = 0 }\]

• 각 상태에 대한 리턴도 위와 같이 표현할 수 있음

3. 테이블 업데이트

• 2단계의 에피소드에서 방문했던 모든 상태에 대해 \(N(s)\)와 \(V(s)\)를 업데이트
  • \(N(s_t) = N(s_t) + 1\)
  • \(V(s_t) = V(s_t) + G_t\)

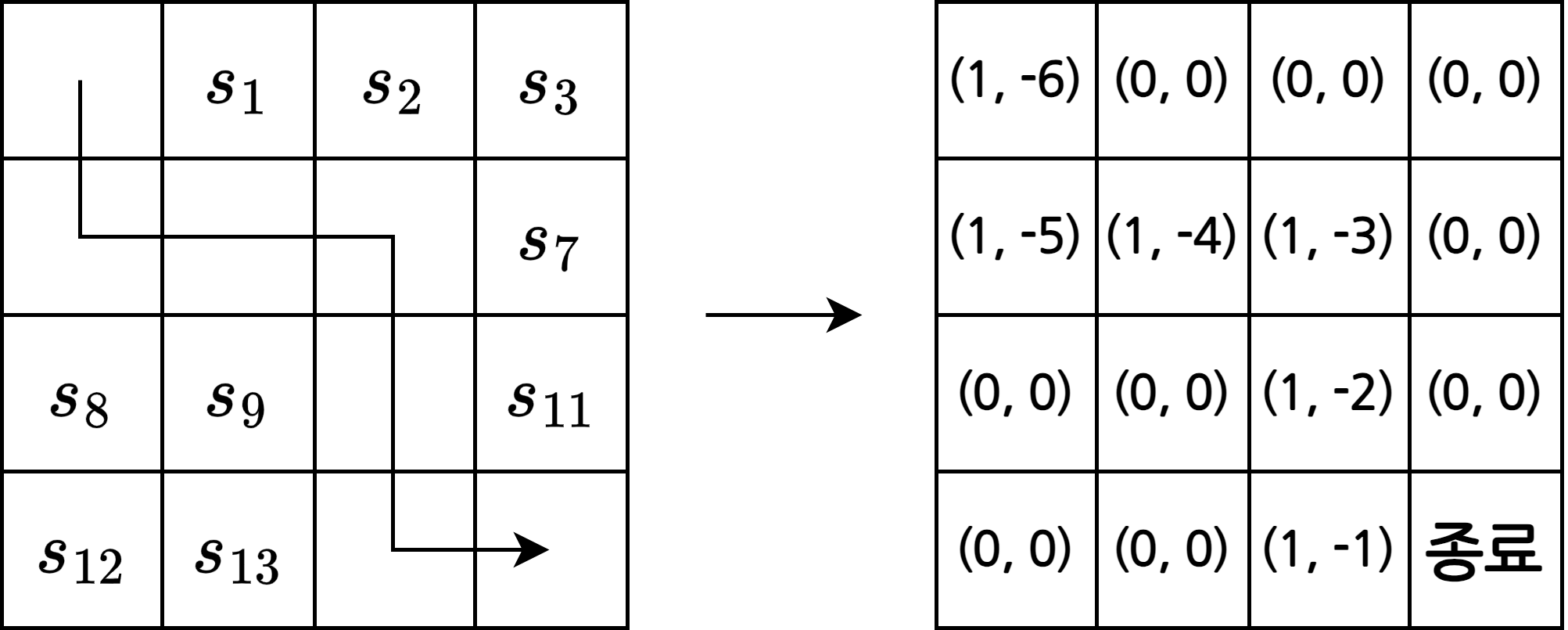
• 만약 왼쪽과 같은 경로로 에피소드를 겪었다면 오른쪽 처럼 값을 업데이트

4. 밸류 계산

• 2단계와 3단계를 충분히 반복한 뒤에 모든 상태에 대해 리턴의 평균을 계산
  • \(v_\pi(s_t) \simeq \frac{V(s_t)}{N(s_t)}\)
  • 이 값이 바로 각 상태의 밸류에 대한 근사치

조금씩 업데이트하는 버전

\[V(s_t) = (1-\alpha)V(s_t) + \alpha G_t\]

• \(\alpha\): 얼마큼 업데이트할지 정하는 파라미터
  • \(\alpha\)가 클수록 한 번에 더 많이 업데이트
• 앞선 방법은 모든 에피소드가 끝난뒤에 평균을 계산하지만 이 방법은 에피소드가 끝날 때마다 값을 업데이트
  • 따라서 \(N(s)\)를 저장할 필요가 없음

\[V(s_t) = V(s_t) + \alpha(G_t - V(s_t))\]

• 식을 변형하면 위와 같이 표현할 수 있음

몬테카를로 학습 구현

Colab 링크

라이브러리 import

import random

환경 class

class GridWorld():
    def __init__(self):
        self.grid_height = 4
        self.grid_width = 4
        self.y = 0
        self.x = 0

    def step(self, a):
        if a == 0:
            self.move_up()
        elif a == 1:
            self.move_down()
        elif a == 2:
            self.move_right()
        elif a == 3:
            self.move_left()
        
        reward = -1
        done = self.is_done()
        return (self.y, self.x), reward, done
    
    def move_up(self):
        self.y -= 1
        if self.y < 0:
            self.y = 0
    
    def move_down(self):
        self.y += 1
        if self.y > self.grid_height - 1:
            self.y = 3

    def move_right(self):
        self.x += 1
        if self.x > self.grid_width - 1:
            self.x = 3
    
    def move_left(self):
        self.x -= 1
        if self.x < 0:
            self.x = 0

    def is_done(self):
        return (self.y == self.grid_height - 1) and (self.x == self.grid_width - 1)

    def get_state(self):
        return (self.y, self.x)
    
    def reset(self):
        self.y = 0;
        self.x = 0
        return (self.y, self.x)

에이전트 class

class Agent():
    def __init__(self):
        pass

    def select_action(self):
        coin = random.random()

        if coin < 0.25:
            action = 0
        elif coin < 0.5:
            action = 1
        elif coin < 0.75:
            action = 2
        else:
            action = 3
        
        return action

메인 함수

def main():
    env = GridWorld()
    agent = Agent()
    data = [[0 for _ in range(env.grid_width)] for _ in range(env.grid_height)]
    gamma = 1.0
    alpha = 0.0001

    for k in range(50000):
        done = False
        history = []
        
        while not done:
            action = agent.select_action()
            (y, x), reward, done = env.step(action)
            history.append((y, x, reward))
        env.reset()

        cum_reward = 0
        for transition in history[::-1]:
            y, x, reward = transition
            data[y][x] += alpha * (cum_reward - data[y][x])
            cum_reward = reward + gamma * cum_reward
    
    for row in data:
        print(row)
    
main()

학습 결과

output
[-59.007577406479726, -56.90183068593777, -54.50167451045022, -51.418768506007595]
[-58.12377551489365, -55.02195434629003, -49.98200088681944, -45.52107387155517]
[-55.16971421190278, -50.91111155623804, -41.27547579390701, -30.110230887686804]
[-53.10501746869333, -45.86982600026009, -30.358163650217517, 0.0]

• Chapter 4. MDP를 알 때의 플래닝에서 했던 반복적 정책 평가의 결과와 비슷한 것을 볼 수 있음

2. Temporal Difference 학습

• 몬테카를로 학습 방법론(MC)와 다르게 매 스텝마다 업데이트
• 추측을 추측으로 업데이트
  • 한 스텝이 지나면, 즉 조금이라도 시간이 흐르면 조금이라도 더 정확할 예측을 할 확률이 높아짐
    • 일요일에 비가 올지 예측할 때, 금요일에 예측하는 것보단 토요일에 예측하는 것이 정확할 확률이 높음
  • 따라서 한 스텝이 지난 뒤의 예측을 이용해 이전 스텝을 업데이트하는 방법
    • MC는 일요일에 도달한 뒤 금요일와 토요일의 예측을 업데이트
    • TD는 금요일에서 토요일로 넘어가자마자 토요일의 예측을 바탕으로 금요일의 예측을 업데이트
• 한마디로 temporal difference, 즉 시간적 차이를 이용해 업데이트하는 방법

이론적 배경

\[v_\pi(s_t) = \mathbb{E}_\pi[r_{t+1} + \gamma v_\pi(s_{t+1})]\]

• 벨만 기대 방정식에 따르면 \(\pi\)를 따를 때 \(s_t\)에서의 밸류는 \(r_{t+1} + \gamma v_\pi(s_{t+1})\)의 기댓값, 즉 평균을 이용해 구할 수 있음
  • 따라서 \(r_{t+1} + \gamma v_\pi(s_{t+1})\)를 구해야 하는 목표, TD 타깃(TD target)이라고 부름

Temporal Difference 학습 알고리즘

• MC와 거의 유사
• 차이점은 업데이트 수식과 업데이트 시점 2가지

업데이트 수식

\[\begin{align} & \textrm{MC}: V(s_t) = V(s_t) + \alpha(G_t - V(s_t)) \\ & \textrm{TD}: V(s_t) = V(s_t) + \alpha(r_{t+1} + \gamma V(s_{t+1}) - V(s_t)) \end{align}\]

• MC의 \(G_t\)를 대신해 TD 타깃에 해당하는 식으로 변경

업데이트 시점

\[s_0 \to s_1 \to s_2 \to \cdots \to s_{T-1} \to s_{T}\]

• MC에서는 종료 상태에 도달한 뒤 나머지 상태를 업데이트
• TD에서는 각 상태가 끝나고 다음 상태로 전이하자마자 업데이트
  • \(s_1\)으로 전이하자마자 \(s_0\) 업데이트

Temporal Difference 학습 구현

Colab 링크

라이브러리 import

• MC와 동일

import random

환경 class

• MC와 동일

class GridWorld():
    def __init__(self):
        self.grid_height = 4
        self.grid_width = 4
        self.y = 0
        self.x = 0

    def step(self, a):
        if a == 0:
            self.move_up()
        elif a == 1:
            self.move_down()
        elif a == 2:
            self.move_right()
        elif a == 3:
            self.move_left()
        
        reward = -1
        done = self.is_done()
        return (self.y, self.x), reward, done
    
    def move_up(self):
        self.y -= 1
        if self.y < 0:
            self.y = 0
    
    def move_down(self):
        self.y += 1
        if self.y > self.grid_height - 1:
            self.y = 3

    def move_right(self):
        self.x += 1
        if self.x > self.grid_width - 1:
            self.x = 3
    
    def move_left(self):
        self.x -= 1
        if self.x < 0:
            self.x = 0

    def is_done(self):
        return (self.y == self.grid_height - 1) and (self.x == self.grid_width - 1)

    def get_state(self):
        return (self.y, self.x)
    
    def reset(self):
        self.y = 0;
        self.x = 0
        return (self.y, self.x)

에이전트 class

• MC와 동일

class Agent():
    def __init__(self):
        pass

    def select_action(self):
        coin = random.random()

        if coin < 0.25:
            action = 0
        elif coin < 0.5:
            action = 1
        elif coin < 0.75:
            action = 2
        else:
            action = 3
        
        return action

메인 함수

def main():
    env = GridWorld()
    agent = Agent()
    data = [[0 for _ in range(env.grid_width)] for _ in range(env.grid_height)]
    gamma = 1.0
    alpha = 0.01

    for k in range(50000):
        done = False
        history = []

        while not done:
            y, x = env.get_state()
            action = agent.select_action()
            (y_prime, x_prime), reward, done = env.step(action)

            data[y][x] += alpha * (reward + gamma * data[y_prime][x_prime] - data[y][x])

        env.reset()

    for row in data:
        print(row)

main()

학습 결과

output
[-60.372567351060965, -58.071167742310585, -54.468654594211905, -51.98825942166704]
[-58.022055012339756, -54.95843650901898, -50.146823583397946, -44.89281950301325]
[-54.835277507356764, -49.801453228430326, -42.10082671507283, -30.151509707475636]
[-53.00296752827345, -46.732310433639526, -33.76168890856503, 0]

3. MC vs TD

학습 시점

• MC: 에피소드가 끝난 후
• TD: 한 스텝이 끝난 후
• MC는 종료 상태가 존재하는 MDP에만 사용 가능
  • Episodic MDP: 종료 상태가 있어 에이전트의 경험이 에피소드 단위로 나뉘어 질 수 있는 MDP
  • Non-Episodic MDP: 종료 상태 없이 하나의 에피소드가 무한히 이어지는 MDP
  • MC는 Episodic MDP에서만, TD는 Episodic MDP와 Non-Episodic MDP 모두에서 사용 가능

편향성(Bias)

• MC: \(v_\pi(s_t)=\mathbb{E}[G_t]\)
  • 여러개의 샘플이 모일 수록 실제와 비슷해짐
    • 여러 \(G_t\)가 모일 수록 실제 \(v_\pi(s_t)\)와 비슷해짐
    • \(G_t\)는 \(v_\pi(s_t)\)의 불편 추정량(unbiased estimate)
  • 편향되어 있지 않음
• TD: \(v_\pi(s_t) = \mathbb{E}[r_{r+1} + \gamma v_\pi(s_{t+1})]\)
  • 실제 \(v_\pi(s_{t+1})\) 대신 학습을 할때 사용하는 \(V_\pi(s_{t+1})\)는 예측 값일 뿐 실제 값과는 다름
  • 따라서 실제 TD 타깃인 \(r_{r+1} + \gamma v_\pi(s_{t+1})\)는 불편 추정량이지만 학습할 때 사용하는 \(r_{r+1} + \gamma V_\pi(s_{t+1})\)는 편향되어 있음

분산(Variance)

• MC: 분산이 큼
• TD: 분산이 작음
• TD가 작은 시간 단위마다 업데이트하기 때문에(확률적 요소가 적기 때문에) 더 정확
  • 서울역에서 부산역 가는 시간을 예측하는 것보다 서울역 앞에 있는 편의점 가는 시간을 예측하는 것이 오차가 더 작음
  • 서울역에서 부산역은 1시간 정도 오차가 날 수 있지만 서울역에서 편의점은 커 봤자 5분 내외임
• 비유적으로 MC는 [-10000, 10000] 분포, TD는 [-1, 1] 분포

종합

• 요즘에 나오는 많은 강화 학습 알고리즘들은 대부분 TD를 바탕으로 개발됨

4. MC와 TD의 중간

• MC는 편향성이 없고 TD는 분산이 작다는 장점이 있음
• TD 타깃: \(r_{t+1} + \gamma V(s_{t+1})\)

“꼭 한 스텝만 가서 평가해야할 이유가 있을까?”

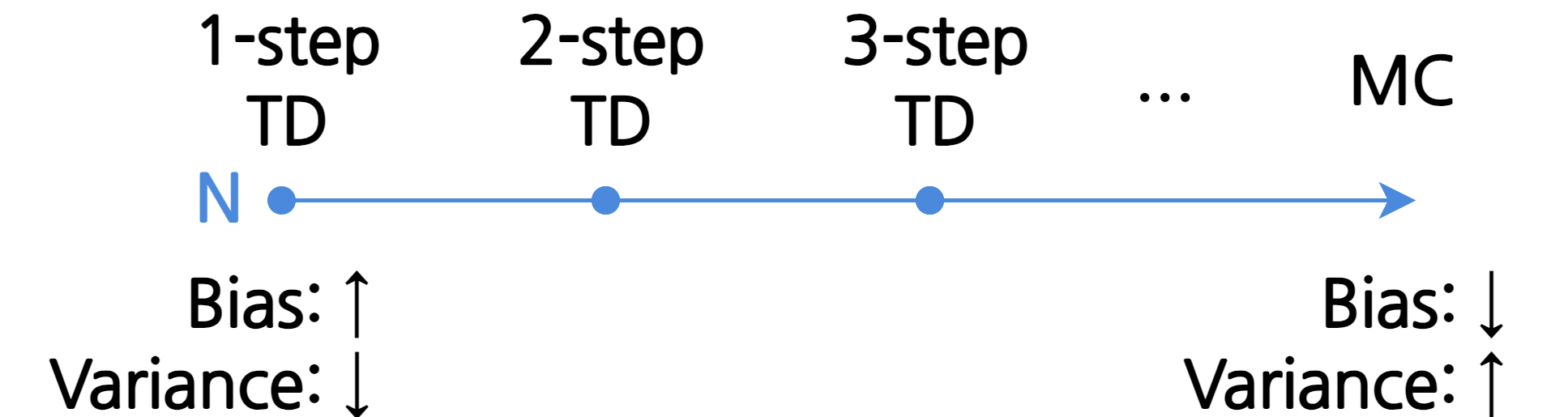
n 스텝 TD

\[\textrm{N = n: } r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots + \gamma^n V(s_{t+n})\]

• n 스텝만큼 진행한 후 가치를 평가

  • 예) 2 스텝만 가서 평가: \(r_{t+1} + \gamma r_{t+2} + \gamma^2 V(s_{t+2})\)

• \(\textrm{N = 1}\)인 경우(TD 타깃을 이용하는 경우)를 TD(0)로 표기하며 TD-zero라고 읽음

• 만약 \(\textrm{N = }\infty\)라면?

  \[\textrm{N = }\infty \textrm{: } r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots + \gamma^{T-1}R_T\]
  • 리턴 \(G_t\)가 됨
  • 즉, MC는 TD의 한 사례인 셈

• MC에 가까워질수록 편향은 낮아지고 분산은 높아짐
• \(\textrm{n}\)을 찾는데에 있어 정답은 없음
  • 따라서 좋은 \(\textrm{n}\)을 선택하는 것이 중요