강화학습 Chapter 6. MDP를 모를 때 최고의 정책 찾기

Posted Jan 4, 2024

Robot

By Seyeon Lee 20 min read

참고 자료

이 글은 [노승은, 바닥부터 배우는 강화 학습, 영진닷컴(2020)]을 바탕으로 작성되었습니다.

1. 몬테카를로 컨트롤

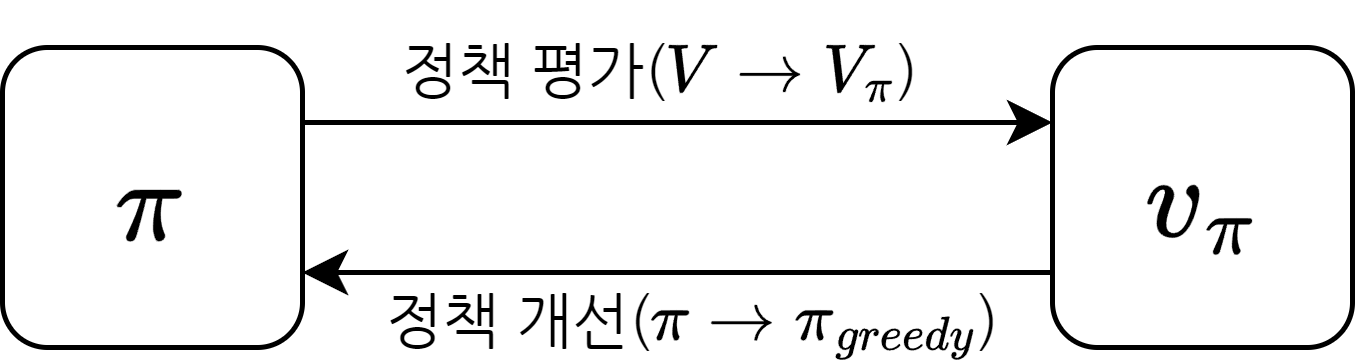
4장에서 배웠던 control 방법인 정책 이터레이션을 그대로 사용하기에는 몇가지 어려움이 있음

정책 이터레이션을 그대로 사용할 수 없는 이유

1. 정책 평가 단계에서 반복적 정책 평가 사용 불가

\[v_\pi(s) = \sum_{a \in A}\pi(a \mid s) \left(r_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a v_\pi(s^\prime) \right)\]

\(r_s^a\)와 \(P_{ss^\prime}^a\)를 모르기 때문
- 실제로 액션을 해서 어디 도착하는지 해봐야 알 수 있음

2. 정책 개선 단계에서 그리디 정책 생성 불가

상태 전이에 대한 정보를 모르기 때문에 더 나은 액션을 선택할 수 없음
- 현재 상태에서 가장 좋은, 즉 도달하게 되는 상태의 밸류가 높은 액션을 선택했지만 어떤 상태에 도달할지 모름

해결 방법

1. MC를 이용해 평가

반복적 정책 평가를 이용해 각 상태의 밸류를 평가할 수 없음
따라서 반복적 정책 평가 대신 MC를 이용해 밸류를 예측

2. V 대신 Q

전이 확률 행렬을 모르기 때문에 \(v(s)\)를 이용해 그리디 정책을 생성할 수 없음
대신 \(q(s, a)\)를 사용
- 액션을 선택했을 때, 어느 상태에 도달할지는 모르지만, 각 액션을 선택하는 것의 밸류는 알 수 있음

3. \(\textrm{greedy}\) 대신 \(\varepsilon-\textrm{greedy}\)

MC를 이용해 \(q(s,a)\)를 계산 → \(q(s, a)\)를 이용해 그리디 정책 생성 → 생성된 그리디 정책에 대한 MC를 이용해 \(q(s, a)\)를 계산 → …
- 만약 모든 \(q(s, a)\) 값을 0으로 초기화 해놓고 학습을 시작하여 \(q(s, a_1)\)의 값이 증가하였다면, 상태 \(s\)에서는 평생 \(a_1\)만 선택됨
- MC는 실제로 실행한 액션의 밸류만 평가할 수 있기 때문에 \(q(s, a_2)\), \(q(s, a_3)\)은 영원히 0이 됨
- 따라서 \(s\)에서 \(a_2\), \(a_3\)를 선택해보지도 않고 \(a_1\)만 선택하게 되므로 최적의 해를 찾지 못할 수도 있음
- 이를 해결하기 위해 탐색(exploration)의 정도를 맞출 필요가 있음

\[\pi(a \mid s) = \begin{cases} 1-\varepsilon & \textrm{if } a^* = \underset{a}{\operatorname{argmax}}q(s, a) \\ \varepsilon & \textrm{otherwise} \end{cases}\]

\(s\)에서의 정책: \(q(s, a)\)가 가장 큰 액션을 선택할 확률이 \(1-\varepsilon\), 나머지 액션을 선택할 확률이 \(\varepsilon\)
- \(\varepsilon\)이 0.1인 경우 0.9의 확률로 \(q(s, a)\)의 값이 가장 높은 액션을 선택하며 0.1의 확률로 무작위 액션을 선택
decaying \(\varepsilon-\textrm{greedy}\): \(\varepsilon\)을 처음에는 높게 설정하고 학습을 하며 점점 줄여주는 방법
- 처음에는 환경에 대해 아는 정보가 없기 때문에 다양한 액션을 하며 정보를 충분히 습득
- 학습이 어느정도 진행된 후에는 얻은 정보를 바탕으로 좋은 액션을 선택

정책 평가 단계에서는 MC를 이용하여 \(q(s, a)\)를 계산
정책 개선 단계에서는 \(q(s, a)\)에 대한 \(\varepsilon-\textrm{greedy}\) 정책을 생성

몬테카를로 컨트롤 구현

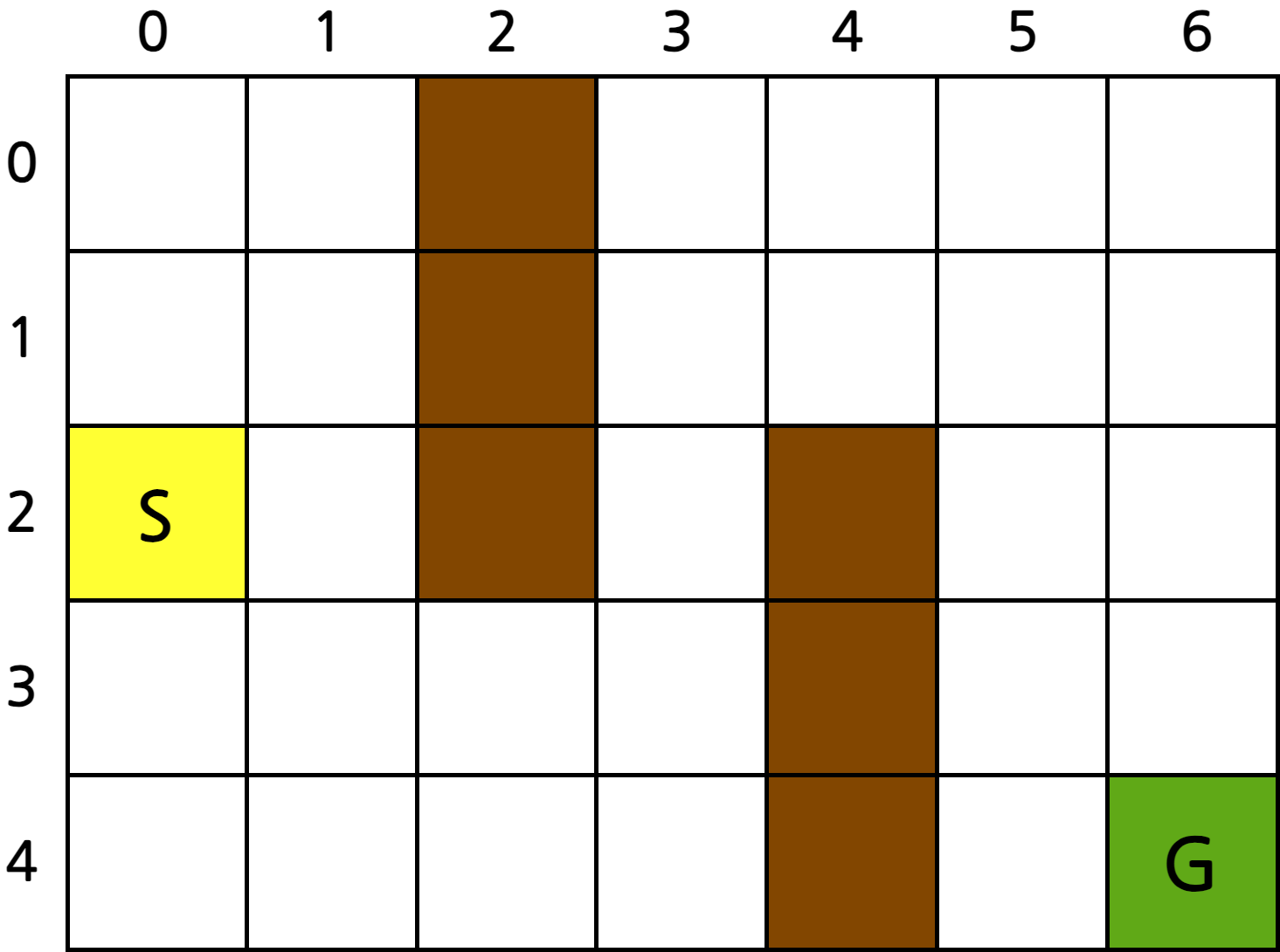
\(S\)에서 출발하여 \(G\)에 도착하면 끝
진한 색이 칠해진 영역은 벽으로 지나갈 수 없음
보상은 스텝마다 -1
수렴할 때까지 \(n\)번 반복
- 한 에피소드를 경험
- 경험을 통해 \(q(s, a)\) 테이블의 값 업데이트(정책 평가)
- 업데이트된 \(q(s, a)\) 테이블을 이용하여 \(\varepsilon-\textrm{greedy}\) 정책 생성

라이브러리 import

  
import random
import numpy as np

환경 class

  
class GridWorld():
    def __init__(self, grid):
        self.grid = grid
        self.grid_height = len(grid)
        self.grid_width = len(grid[0])

        self.y = 2
        self.x = 0

    def step(self, a):
        if a == 0:
            self.move_up()
        elif a == 1:
            self.move_down()
        elif a == 2:
            self.move_right()
        elif a == 3:
            self.move_left()

        reward = -1
        done = self.is_done()
        return (self.y, self.x), reward, done

    def move_up(self):
        self.y -= 1
        if self.y < 0 or self.grid[self.y][self.x] == 2:
            self.y += 1

    def move_down(self):
        self.y += 1
        if self.y > self.grid_height - 1 or self.grid[self.y][self.x] == 2:
            self.y -= 1

    def move_right(self):
        self.x += 1
        if self.x > self.grid_width - 1 or self.grid[self.y][self.x] == 2:
            self.x -= 1

    def move_left(self):
        self.x -= 1
        if self.x < 0 or self.grid[self.y][self.x] == 2:
            self.x += 1

    def is_done(self):
        return self.grid[self.y][self.x] == 1

    def get_state(self):
        return (self.y, self.x)

    def reset(self):
        self.y = 0;
        self.x = 0
        return (self.y, self.x)

에이전트 class

  
class QAgent():
    def __init__(self):
        self.q_table = np.zeros((5, 7, 4))
        self.eps = 0.9
        self.alpha = 0.01

    def select_action(self, s):
        y, x = s
        coin = random.random()
        if coin < self.eps:
            action = random.randint(0, 3)
        else:
            action_val = self.q_table[y, x, :]
            action = np.argmax(action_val)
        return action

    def update_table(self, history):
        cum_reward = 0
        for transition in history[::-1]:
            s, a, r, s_prime = transition
            y, x = s

            self.q_table[y, x, a] += self.alpha * (cum_reward - self.q_table[y, x, a])

            cum_reward += r
            
    def anneal_eps(self):
        self.eps -= 0.03
        self.eps = max(self.eps, 0.1)

    def show_table(self):
        q_lst = self.q_table.tolist()
        num2arrow = ['↑', '↓', '→', '←']
        data = np.zeros((5, 7)).tolist()
        for row_idx, row_val in enumerate(q_lst):
            for col_idx, col_val in enumerate(row_val):
                action = np.argmax(col_val)
                data[row_idx][col_idx] = num2arrow[action]
        print(*data, sep='\n')

메인 함수

  
def main():
    grid = [
        [0, 0, 2, 0, 0, 0, 0],
        [0, 0, 2, 0, 0, 0, 0],
        [0, 0, 2, 0, 2, 0, 0],
        [0, 0, 0, 0, 2, 0, 0],
        [0, 0, 0, 0, 2, 0, 1]
    ]
    env = GridWorld(grid)
    agent = QAgent()

    for n_epi in range(10000):
        done = False
        history = []

        s = env.reset()
        while not done:
            a = agent.select_action(s)
            s_prime, r, done = env.step(a)
            history.append((s, a, r, s_prime))
            s = s_prime
        agent.update_table(history)
        agent.anneal_eps()

    agent.show_table()

main()

학습 결과

['↓', '→', '↑', '→', '↓', '←', '↓']
['↓', '←', '↑', '→', '→', '→', '↓']
['→', '↓', '↑', '↑', '↑', '↓', '↓']
['→', '→', '→', '↑', '↑', '↓', '↓']
['↓', '↑', '↑', '↓', '↑', '→', '↑']

2. TD 컨트롤 1 - SARSA

MC 대신 TD

정책 평가 단계에서 MC 대신 TD를 사용

\[\begin{align} & v_\pi(s_t) = \mathbb{E}_\pi[r_{t+1} + \gamma v_\pi(s_{t+1})] \\ & q_\pi(s_t, a_t) = \mathbb{E}_\pi[r_{t+1} + \gamma q_\pi(s_{t+1}, a_{t+1})] \end{align}\]

TD를 이용해 \(v\) 대신 \(q\)를 업데이트

\[\begin{align} & V(S) = V(S) + \alpha(R + \gamma V(S^\prime) - V(S)) \\ & Q(S, A) = Q(s, A) + \alpha(R + \gamma Q(S^\prime, A^\prime) - Q(S, A)) \end{align}\]

한 스텝마다 생성된 데이터를 이용해 TD 타깃을 계산하여 기존의 테이블의 값을 조금씩 업데이트

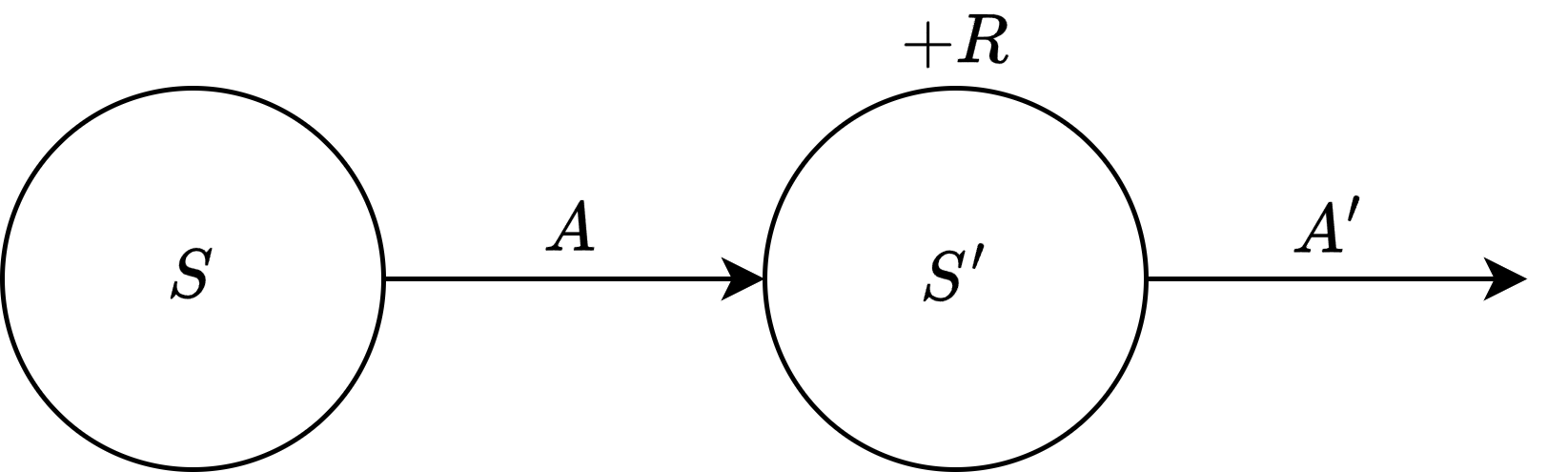
상태 \(s\)에서 액션 \(a\)를 선택하여 보상 \(r\)을 받고 상태 \(s^\prime\)에 도착하여 다음 액션 \(a^\prime\)를 선택
- 이 데이터를 이용해 \(q(s, a)\)를 조금씩 업데이트

SARSA 구현

라이브러리 import

몬테카를로 컨트롤과 같음

  
import random
import numpy as np

환경 class

몬테카를로 컨트롤과 같음

  
class GridWorld():
    def __init__(self, grid):
        self.grid = grid
        self.grid_height = len(grid)
        self.grid_width = len(grid[0])

        self.y = 2
        self.x = 0

    def step(self, a):
        if a == 0:
            self.move_up()
        elif a == 1:
            self.move_down()
        elif a == 2:
            self.move_right()
        elif a == 3:
            self.move_left()

        reward = -1
        done = self.is_done()
        return (self.y, self.x), reward, done

    def move_up(self):
        self.y -= 1
        if self.y < 0 or self.grid[self.y][self.x] == 2:
            self.y += 1

    def move_down(self):
        self.y += 1
        if self.y > self.grid_height - 1 or self.grid[self.y][self.x] == 2:
            self.y -= 1

    def move_right(self):
        self.x += 1
        if self.x > self.grid_width - 1 or self.grid[self.y][self.x] == 2:
            self.x -= 1

    def move_left(self):
        self.x -= 1
        if self.x < 0 or self.grid[self.y][self.x] == 2:
            self.x += 1

    def is_done(self):
        return self.grid[self.y][self.x] == 1

    def get_state(self):
        return (self.y, self.x)

    def reset(self):
        self.y = 0;
        self.x = 0
        return (self.y, self.x)

에이전트 class

update_table 함수만 수정

  
class QAgent():
    def __init__(self):
        self.q_table = np.zeros((5, 7, 4))
        self.eps = 0.9
        self.alpha = 0.1

    def select_action(self, s):
        y, x = s
        coin = random.random()
        if coin < self.eps:
            action = random.randint(0, 3)
        else:
            action_val = self.q_table[y, x, :]
            action = np.argmax(action_val)
        return action

    def update_table(self, transition):
        s, a, r, s_prime = transition
        y, x = s
        next_y, next_x = s_prime
        a_prime = self.select_action(s_prime)

        self.q_table[y, x, a] += self.alpha * (r + self.q_table[next_y, next_x, a_prime] - self.q_table[y, x, a])

    def anneal_eps(self):
        self.eps -= 0.03
        self.eps = max(self.eps, 0.1)

    def show_table(self):
        q_lst = self.q_table.tolist()
        num2arrow = ['↑', '↓', '→', '←']
        data = np.zeros((5, 7)).tolist()
        for row_idx, row_val in enumerate(q_lst):
            for col_idx, col_val in enumerate(row_val):
                action = np.argmax(col_val)
                data[row_idx][col_idx] = num2arrow[action]
        print(*data, sep='\n')

메인 함수

  
def main():
    grid = [
        [0, 0, 2, 0, 0, 0, 0],
        [0, 0, 2, 0, 0, 0, 0],
        [0, 0, 2, 0, 2, 0, 0],
        [0, 0, 0, 0, 2, 0, 0],
        [0, 0, 0, 0, 2, 0, 1]
    ]
    env = GridWorld(grid)
    agent = QAgent()

    for n_epi in range(10000):
        done = False

        s = env.reset()
        while not done:
            a = agent.select_action(s)
            s_prime, r, done = env.step(a)
            agent.update_table((s, a, r, s_prime))
            s = s_prime
        agent.anneal_eps()

    agent.show_table()

main()

학습 결과

['↓', '↓', '↑', '↓', '→', '→', '↓']
['→', '↓', '↑', '→', '→', '↓', '↓']
['↓', '↓', '↑', '↑', '↑', '↓', '↓']
['→', '→', '→', '↑', '↑', '↓', '↓']
['→', '→', '→', '↑', '↑', '→', '↑']

3. TD 컨트롤 2 - Q러닝

처음으로 딥러닝과 결합되어 성과를 보여준 알고리즘
“Human-level control through deep reinforcement learning”이라는 제목의 논문이 2015년에 출판됨
딥러닝과 강화 학습 알고리즘인 Q러닝을 결합하여 고전 비디오 게임인 아타리 2600을 사람 수준으로 플레이하는 에이전트를 만듦

Off-Policy와 On-Policy

타깃 정책(target policy): 강화하고자 하는 목표가 되는 정책
행동 정책(behavior policy): 실제로 환경과 상호 작용하며 경험을 쌓는 정책
On-Policy: 타깃 정책과 행동 정책이 같은 경우
Off-Policy: 타깃 정책과 행동 정책이 다른 경우
예)
- 게임을 플레이하는 A와 A가 플레이하는 것을 지켜보는 B가 있을 때, A는 On-Policy, B는 Off-Policy
- A
  - 타깃 정책: 자신의 정책
  - 행동 정책: 자신의 정책
- B
  - 타깃 정책: 자신의 정책
  - 행동 정책: A의 정책
Off-Policy와 지도 학습의 차이점
- 지도 학습: A의 정책을 보고 무조건 정답이라고 생각
  - A의 행동 중 좋지 않은 행동이 있어도 그대로 따라할 가능성이 높음
- Off-Policy: A의 정책이 틀릴 수도 있다는 점을 인지
  - A의 행동 중 좋지 않은 행동이 있다면 이를 보완할 가능성이 높음

Off-Policy 학습의 장점

과거의 경험 재사용

On-Policy의 경우 타깃 정책과 행동 정책이 같아야 하기 때문에 다른 정책이 경험한 데이터를 사용할 수 없음
- 여러번의 경험을 통해 \(\pi_0\)을 학습시켜 \(\pi_1\)으로 업데이트 했을 때, \(\pi_1\)을 학습시키려면 다시 경험을 쌓아야 함
Off-Policy의 경우 다른 정책이 경험한 데이터를 학습에 사용할 수 있음
- 여러번의 경험을 통해 \(\pi_0\)을 학습시켜 \(\pi_1\)으로 업데이트 했을 때, \(\pi_1\)을 학습시키기 위해 \(\pi_0\)이 경험한 데이터를 사용할 수 있음

사람의 데이터로부터 학습 가능

초기에는 랜덤 정책을 이용하기 때문에 이를 통해 얻는 데이터의 질이 매우 낮음
따라서 전문가(사람)가 만든 데이터를 이용해 학습하면 초기의 무의미한 행동을 하는 단계를 빨리 벗어날 수 있음

일대다, 다대일 학습이 가능

단 1개의 정책이 쌓은 경험만을 가지고 여러개의 정책을 학습시킬 수 있음
여러개의 정책이 쌓은 경험을 가지고 한개의 정책을 학습시킬 수도 있음

Q러닝의 이론적 배경 - 벨만 최적 방정식

\[\begin{align} & q_*(s, a) = \max_\pi q_\pi(s, a) \\ & \pi_* = \underset{a}{\operatorname{argmax}} q_*(s^\prime, a^\prime) \end{align}\]

\(q_*\)를 알게 되는 순간 MDP에서 순간마다 최적의 행동을 선택하며 움직일 수 있음
- 따라서 \(q_*\)를 찾는 것이 목표

\[\begin{align} & q_*(s, a) = r_s^a + \gamma \sum_{s^\prime \in S}P_{ss^\prime}^a \max_{a^\prime}q_*(s^\prime, a^\prime) \\ & q_*(s, a) = \mathbb{E}_{s^\prime}[r + \gamma \max_{a^\prime}q_*(s^\prime, a^\prime)] \end{align}\]

TD 타깃: \(r + \gamma \underset{a^\prime}{\max}q_*(s^\prime, a^\prime)\)

\[Q(S, A) = Q(S, A) + \alpha(R + \gamma \max_{A^\prime} Q(S^\prime, A^\prime) - Q(S, A))\]

SARSA vs Q러닝

SARSA: on-policy
- 행동 정책: \(\varepsilon-\textrm{Greedy}(Q)\)
- 타깃 정책: \(\varepsilon-\textrm{Greedy}(Q)\)
- 벨만 기대 방정식: \(q_\pi(s_t, a_t) = \mathbb{E}_\pi[r_{t+1} + \gamma q_\pi(s_{t+1}, a_{t+1})]\)
Q러닝: off-policy
- 행동 정책: \(\varepsilon-\textrm{Greedy}(Q)\)
- 타깃 정책: \(\textrm{Greedy}(Q)\)
- 벨만 최적 방정식: \(q_*(s, a) = \mathbb{E}_{s^\prime}[r + \gamma \underset{a^\prime}{\max}q_*(s^\prime, a^\prime)]\)
SARSA는 \(\mathbb{E}_\pi\), Q러닝은 \(\mathbb{E}_{s^\prime}\)
- \(\mathbb{E}_\pi\): 정책 함수 \(\pi\)를 따르는 경로에 대한 기댓값
  - 따라서 \(\mathbb{E}_\pi\)를 얻기 위해서는 반드시 \(\pi\)에 의한 액션 선택이 있어야 함
- \(\mathbb{E}_{s^\prime}\): 상태가 \(s^\prime\)일 때의 기댓값
  - 따라서 \(\pi\)는 중요하지 않음

Q러닝 구현

Colab 링크

라이브러리 import

몬테카를로 컨트롤과 같음

  
import random
import numpy as np

환경 class

몬테카를로 컨트롤과 같음

  
class GridWorld():
    def __init__(self, grid):
        self.grid = grid
        self.grid_height = len(grid)
        self.grid_width = len(grid[0])

        self.y = 2
        self.x = 0

    def step(self, a):
        if a == 0:
            self.move_up()
        elif a == 1:
            self.move_down()
        elif a == 2:
            self.move_right()
        elif a == 3:
            self.move_left()

        reward = -1
        done = self.is_done()
        return (self.y, self.x), reward, done

    def move_up(self):
        self.y -= 1
        if self.y < 0 or self.grid[self.y][self.x] == 2:
            self.y += 1

    def move_down(self):
        self.y += 1
        if self.y > self.grid_height - 1 or self.grid[self.y][self.x] == 2:
            self.y -= 1

    def move_right(self):
        self.x += 1
        if self.x > self.grid_width - 1 or self.grid[self.y][self.x] == 2:
            self.x -= 1

    def move_left(self):
        self.x -= 1
        if self.x < 0 or self.grid[self.y][self.x] == 2:
            self.x += 1

    def is_done(self):
        return self.grid[self.y][self.x] == 1

    def get_state(self):
        return (self.y, self.x)

    def reset(self):
        self.y = 0;
        self.x = 0
        return (self.y, self.x)

에이전트 class

update_table 함수와 anneal_eps 함수 수정

  
class QAgent():
    def __init__(self):
        self.q_table = np.zeros((5, 7, 4))
        self.eps = 0.9
        self.alpha = 0.1

    def select_action(self, s):
        y, x = s
        coin = random.random()
        if coin < self.eps:
            action = random.randint(0, 3)
        else:
            action_val = self.q_table[y, x, :]
            action = np.argmax(action_val)
        return action

    def update_table(self, transition):
        s, a, r, s_prime = transition
        y, x = s
        next_y, next_x = s_prime

        self.q_table[y, x, a] += self.alpha * (r + np.amax(self.q_table[next_y, next_x, :]) - self.q_table[y, x, a])

    def anneal_eps(self):
        self.eps -= 0.01
        self.eps = max(self.eps, 0.2)

    def show_table(self):
        q_lst = self.q_table.tolist()
        num2arrow = ['↑', '↓', '→', '←']
        data = np.zeros((5, 7)).tolist()
        for row_idx, row_val in enumerate(q_lst):
            for col_idx, col_val in enumerate(row_val):
                action = np.argmax(col_val)
                data[row_idx][col_idx] = num2arrow[action]
        print(*data, sep='\n')

메인 함수

  
def main():
    grid = [
        [0, 0, 2, 0, 0, 0, 0],
        [0, 0, 2, 0, 0, 0, 0],
        [0, 0, 2, 0, 2, 0, 0],
        [0, 0, 0, 0, 2, 0, 0],
        [0, 0, 0, 0, 2, 0, 1]
    ]
    env = GridWorld(grid)
    agent = QAgent()

    for n_epi in range(10000):
        done = False

        s = env.reset()
        while not done:
            a = agent.select_action(s)
            s_prime, r, done = env.step(a)
            agent.update_table((s, a, r, s_prime))
            s = s_prime
        agent.anneal_eps()

    agent.show_table()

main()

학습 결과

['↓', '↓', '↑', '↓', '↓', '↓', '↓']
['↓', '↓', '↑', '→', '→', '↓', '↓']
['↓', '↓', '↑', '↑', '↑', '↓', '↓']
['→', '→', '→', '↑', '↑', '↓', '↓']
['→', '↑', '↑', '↑', '↑', '→', '↑']

Artificial Intelligence, Reinforcement Learning

AI RL

This post is licensed under CC BY 4.0 by the author.

참고 자료

1. 몬테카를로 컨트롤

정책 이터레이션을 그대로 사용할 수 없는 이유

1. 정책 평가 단계에서 반복적 정책 평가 사용 불가

2. 정책 개선 단계에서 그리디 정책 생성 불가

해결 방법

1. MC를 이용해 평가

2. V 대신 Q

3. \(\textrm{greedy}\) 대신 \(\varepsilon-\textrm{greedy}\)

몬테카를로 컨트롤 구현

Colab 링크

라이브러리 import

환경 class

에이전트 class

메인 함수

학습 결과

2. TD 컨트롤 1 - SARSA

MC 대신 TD

SARSA 구현

Colab 링크

라이브러리 import

환경 class

에이전트 class

메인 함수

학습 결과

3. TD 컨트롤 2 - Q러닝

Off-Policy와 On-Policy

Off-Policy 학습의 장점

과거의 경험 재사용

사람의 데이터로부터 학습 가능

일대다, 다대일 학습이 가능

Q러닝의 이론적 배경 - 벨만 최적 방정식

SARSA vs Q러닝

Q러닝 구현

Colab 링크

라이브러리 import

환경 class

에이전트 class

메인 함수

학습 결과

Trending Tags