강화학습 Chapter 7. 가치 기반 에이전트
참고 자료
이 글은 [노승은, 바닥부터 배우는 강화 학습, 영진닷컴(2020)]을 바탕으로 작성되었습니다.
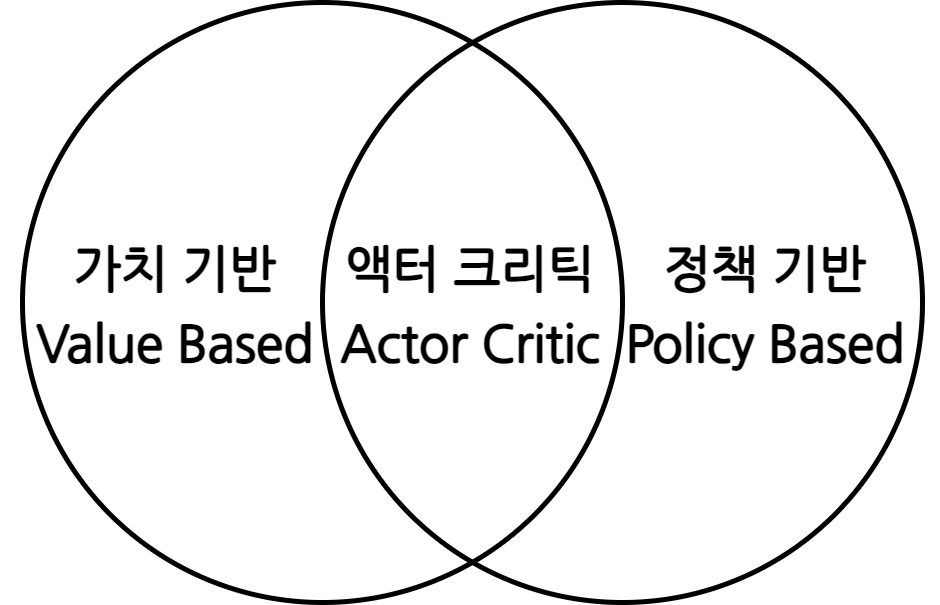
가치 기반, 정책 기반, 액터-크리틱
가치 기반(value-based) 에이전트
정책 기반(policy-based) 에이전트
- 정책 함수를 보고 액션을 선택
- 밸류를 보고 액션을 선택하지 않기 때문에 따로 가치 함수가 없음
- \(\pi\)를 이용해 MDP 안에서 경험을 쌓고 이를 이용해 \(\pi\)를 강화
- 이 과정에서 가치 함수는 쓰이지 않고 가치를 평가하지도 않음
액터 크리틱(actor-critic)
- 가치 함수와 정책 함수를 모두 사용
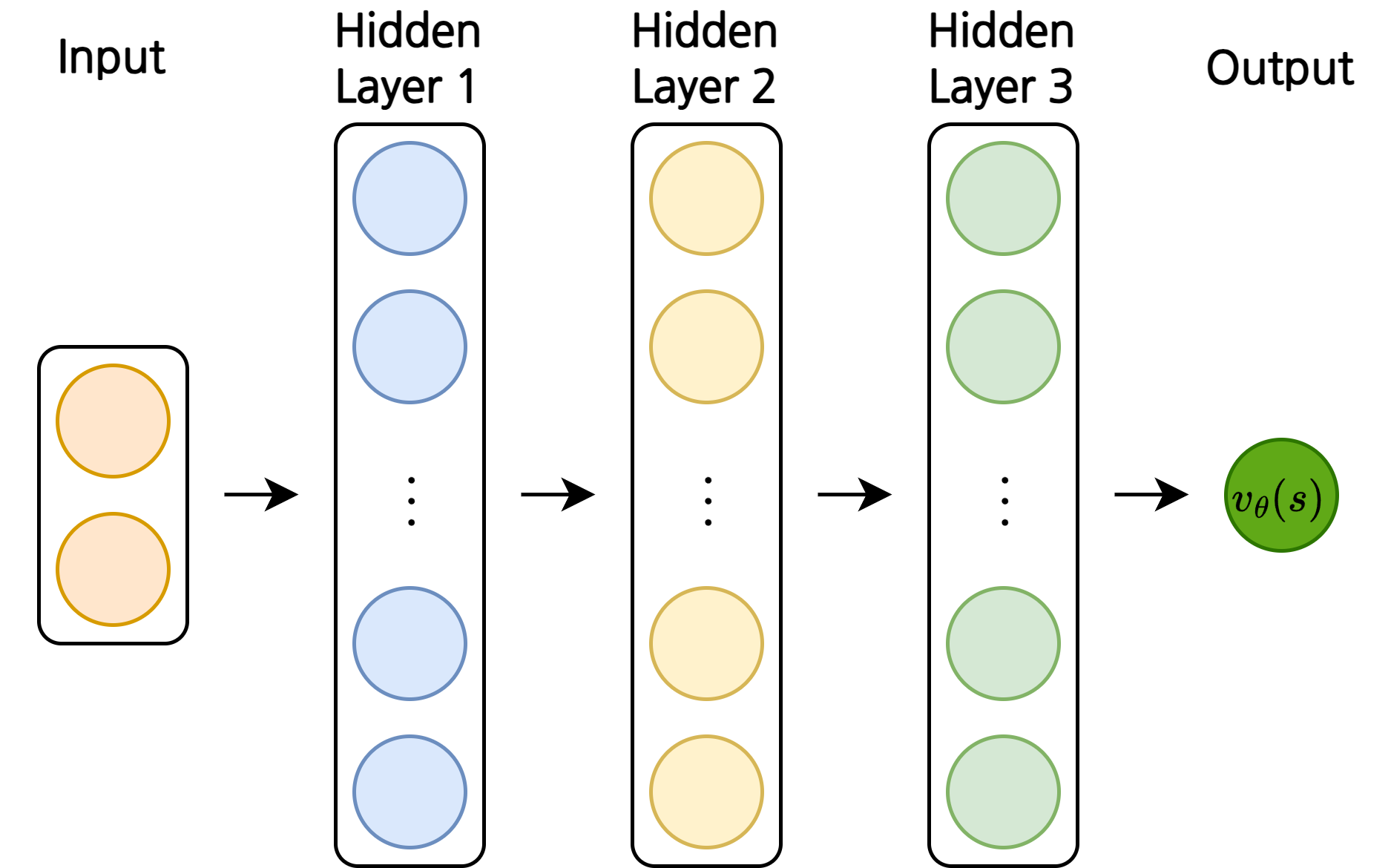
1. 밸류 네트워크의 학습
- 뉴럴넷으로 이루어진 가치 함수 \(v_\theta(s)\)를 밸류 네트워크(value network)라고 부름
- 길이가 2인 벡터 인풋 \(s\)를 받아 정책 \(\pi\)를 따랐을 때의 밸류를 리턴
- 정확히는 \(v_{\theta, \pi}(s)\)로 표현
- \(\theta\): 뉴럴넷의 파라미터
- 예) 파라미터가 100만개라면 \(\theta\)는 길이가 100만인 벡터
- 처음에는 랜덤으로 초기화
- 적절한 \(\theta\)를 찾아 각 상태에 맞는 밸류를 리턴하도록 하는 것이 목표
손실 함수
\[L(\theta) = (v_{true}(s) - v_\theta(s))^2\]- 상태별 밸류의 값을 \(v_{true}(s)\)라고 가정
- 어떤 상태에 대해 \(L(\theta)\)를 최소화 할지 알 수 없음
- 모든 상태를 방문하는 것은 현실적으로 거의 불가능 하기 때문에 계산하기 어려움
- 기댓값을 이용하여 \(\pi\)를 통해 방문했던 \(s\)에 대해서만 \((v_{true}(s) - v_\theta(s))^2\) 값을 계산하라는 의미
그라디언트
\[\nabla_\theta L(\theta) = -\mathbb{E}_\pi \left[ (v_{true}(s) - v_\theta(s)) \nabla_\theta v_\theta(s) \right]\]- 앞에 곱해지는 \(2\)는 생략
- 학습률 \(\alpha\)를 통해 조절할 수 있음
- \(\pi\)를 이용해 여러번 샘플을 뽑아 계산하면 결국 좌변과 우변은 거의 같아짐
- 모든 샘플에 대해 위 과정을 반복
\(v_{true}(s)\)를 구하는 방법
1. 몬테카를로 리턴
\[\begin{align} & L(\theta) = \mathbb{E}_\pi \left[ (G_t - v_\theta(s_t))^2 \right] \\ & \theta^\prime = \theta + \alpha (G_t - v_\theta(s)) \nabla_\theta v_\theta(s) \end{align}\]- 몬테카를로 학습처럼 가치 함수의 정의가 \(G_t\)의 기댓값이므로 대체 가능
- 에피소드가 끝나야 리턴을 계산할 수 있으므로 실시간 업데이트 불가
2. TD 타깃
\[\begin{align} & L(\theta) = \mathbb{E}_\pi \left[ (r_{t+1} + \gamma v_\theta(s_{t+1}) - v_\theta(s_t))^2 \right] \\ & \theta^\prime = \theta + \alpha (r_{t+1} + \gamma v_\theta(s_{t+1}) - v_\theta(s)) \nabla_\theta v_\theta(s) \end{align}\]- \(r_{t+1} + \gamma v_\theta(s_{t+1})\)는 변수가 아닌 상수
- 매 스텝마다 실시간 업데이트 가능
2. 딥 Q러닝
이론적 배경 - Q러닝
\[\begin{align} & Q_*(s, a) = \mathbb{E}_{s^\prime} \left[ r + \gamma \underset{a^\prime}{\operatorname{max}}Q_*(s^\prime, a^\prime) \right] \\ & Q(s, a) = Q(s, a) + \alpha (r + \gamma \underset{a^\prime}{\operatorname{max}} Q(s^\prime, a^\prime) - Q(s, a)) \end{align}\]- Q러닝의 업데이트 수식
- \(Q_\theta(s, a)\)
- Q러닝의 테이블 업데이트 수식을 뉴럴넷으로 확장
- \(\theta\)는 뉴럴넷의 파라미터 벡터
- \(r + \gamma \underset{a^\prime}{\operatorname{max}}Q_\theta(s^\prime, a^\prime)\)를 정답으로 보고 추측치인 \(Q_\theta(s, a)\)와의 차이를 줄이는 방향으로 업데이트
- 이 식을 통해 \(Q_\theta(s, a)\)는 점점 \(Q_*(s, a)\)에 가까워짐
- pytorch나 tensorflow 등의 라이브러리에서는 \(L(\theta)\)에 대한 그라디언트를 자동으로 계산하여 \(\theta\)를 업데이트 해주기 때문에 이 단계까지 직접 미분을 할 필요는 없음
딥 Q러닝 pseudo code
- \(Q_\theta\)의 파라미터 \(\theta\)를 초기화
- 에이전트의 상태 \(s\)를 초기화(\(s \leftarrow s_0\))
- 에피소드가 끝날 때까지 다음을 반복
- \(Q_\theta\)에 대한 \(\varepsilon - \textrm{greedy}\)를 이용하여 액션 \(a\)를 선택
- \(a\)를 실행하여 \(r\)과 \(s^\prime\) 관측
- \(s^\prime\)에서 \(Q_\theta\)에 대한 \(\textrm{greedy}\)를 이용하여 액션 \(a^\prime\)를 선택
- \(\theta\) 업데이트: \(\theta^\prime = \theta + \alpha (r + \gamma \underset{a^\prime}{\operatorname{max}}Q_\theta(s^\prime, a^\prime) - Q_\theta(s, a)) \nabla_\theta(s, a)\)
- \(s \leftarrow s^\prime\)
- 에피소드가 끝나면 다시 2번으로 돌아가서 \(\theta\)가 수렴할 때까지 반복
- 3-1: 실제 액션을 선택, 3-3: TD 타깃의 값을 계산하기 위한 액션을 선택
익스피리언스 리플레이와 타깃 네트워크
익스피리언스 리플레이(Experience Replay)
- 에이전트의 경험을 리플레이 버퍼에 쌓아 나중에 사용하는 방법
- 하나의 상태전이 \(e_t\)는 \((s_t, a_t, r_t, s_{t+1})\)로 표현 가능
- 상태 \(s_t\)에서 액션 \(a_t\)를 했더니 보상 \(r_t\)를 받고 다음 상태 \(s_{t+1}\)에 도달했다는 의미
- 이런 낱개의 데이터를 리플레이 버퍼에 저장
- 리플레이 버퍼: 가장 최근의 데이터 n개를 저장하는 버퍼
- 저장된 데이터 중 랜덤하게 뽑아 학습에 사용
- 하나의 상태전이 \(e_t\)는 \((s_t, a_t, r_t, s_{t+1})\)로 표현 가능
- 서로 다른 에피소드에서 발생한 여러 경험이 랜덤하게 선택되므로 데이터 사이의 상관성이 작아짐
- 따라서 효율적으로 학습 가능
- 서로 연관이 없기 때문에 데이터를 재사용 할 수 있음
- 따라서 효율적으로 학습 가능
별도의 타깃 네트워크(Target Network)
\[L(\theta) = \mathbb{E} \left[ \left( r + \gamma \underset{a^\prime}{\operatorname{max}}Q_\theta(s^\prime, a^\prime) - Q_\theta(s, a) \right)^2 \right]\]- \(L(\theta)\)는 정답과 추측 사이의 차이이며, 이를 줄이는 방향으로 \(\theta\)가 업데이트 됨
- 하지만 정답인 \(r + \gamma \underset{a^\prime}{\operatorname{max}}Q_\theta(s^\prime, a^\prime)\)는 \(\theta\)에 의존적이기 때문에 불안정적임
- 이 문제를 해결하기 위해 정답과 추측, 두 개의 네트워크를 준비
- 우선 정답 네트워크의 파라미터를 고정(\(\theta_t^-\))
- 추측 네트워크의 파라미터를 학습시켜 업데이트
- 일정 주기마다 고정시킨 정답 네트워크의 파라미터를 추측 네트워크의 파라미터로 교체
DQN 구현
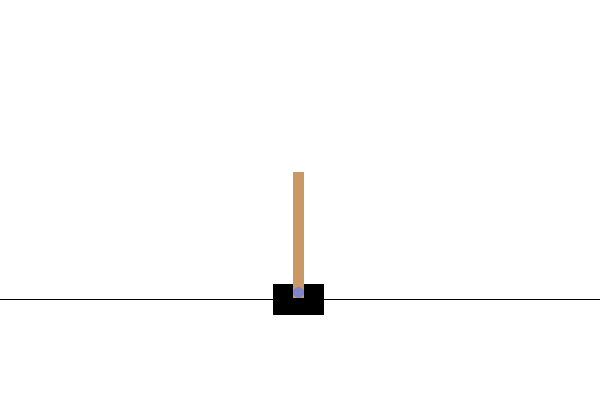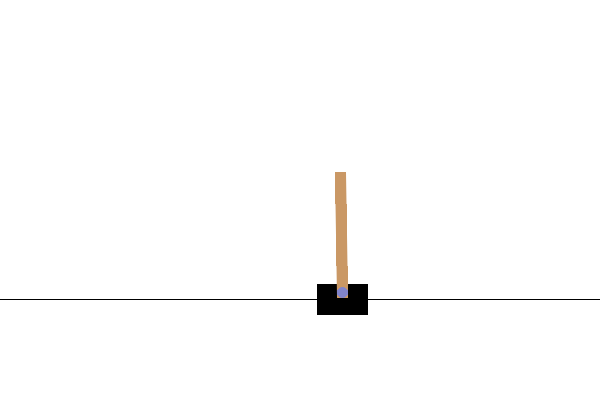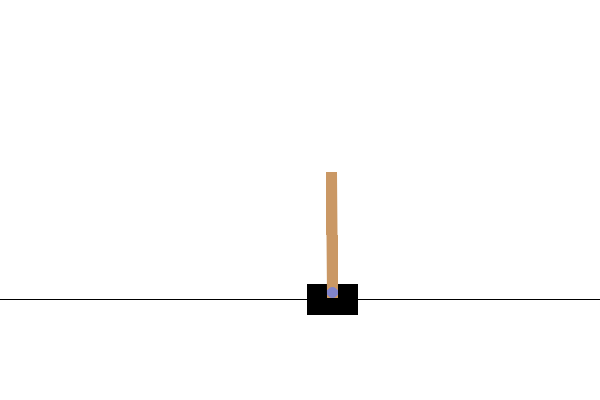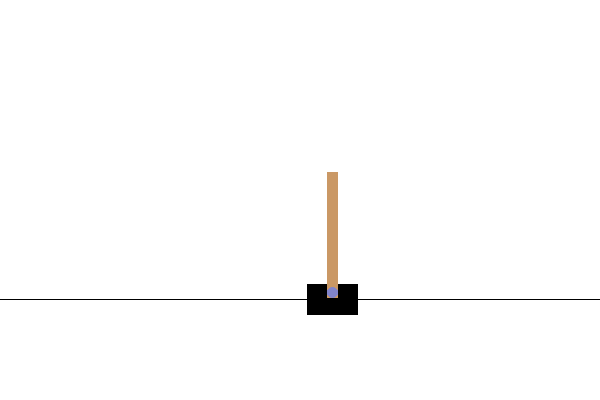
- 환경: OpenAI Gym의 카트폴
- 카트를 잘 밀어서 막대가 넘어지지 않도록 균형을 잡는 문제
- 막대가 12도 이상 기울어지거나 카트가 범위 밖으로 넘어가면 종료
- 상태: (카트 위치, 카트 속도, 막대 각도, 막대 각속도)
- 보상: 스텝마다 +1
- 에이전트
- 액션: 일정한 힘으로 왼쪽 또는 오른쪽
Colab 링크
라이브러리 import
1
2
3
4
5
6
7
8
import gym
import collections
import random
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
하이퍼 파라미터 정의
1
2
3
4
learning_rate = 0.0005
gamma = 0.98
buffer_limit = 50000
batch_size = 32
리플레이 버퍼 클래스
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class ReplayBuffer():
def __init__(self):
self.buffer = collections.deque(maxlen=buffer_limit)
def put(self, transition):
self.buffer.append(transition)
def sample(self, n):
mini_batch = random.sample(self.buffer, n)
s_lst, a_lst, r_lst, s_prime_lst, done_mask_lst = [], [], [], [], []
for transition in mini_batch:
s, a, r, s_prime, done_mask = transition
s_lst.append(s)
a_lst.append([a])
r_lst.append([r])
s_prime_lst.append(s_prime)
done_mask_lst.append([done_mask]);
return torch.tensor(s_lst, dtype=torch.float), torch.tensor(a_lst), torch.tensor(r_lst), torch.tensor(s_prime_lst, dtype=torch.float), torch.tensor(done_mask_lst)
def size(self):
return len(self.buffer);
Q 밸류 네트워크 클래스
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Qnet(nn.Module):
def __init__(self):
super(Qnet, self).__init__()
self.fc1 = nn.Linear(4, 128)
self.relu1 = nn.ReLU()
self.fc2 = nn.Linear(128, 128)
self.relu2 = nn.ReLU()
self.fc3 = nn.Linear(128, 2)
def forward(self, x):
fc1 = self.fc1(x)
relu1 = self.relu1(fc1)
fc2 = self.fc2(relu1)
relu2 = self.relu2(fc2)
fc3 = self.fc3(relu2)
return fc3
def sample_action(self, obs, epsilon):
out = self.forward(obs)
coin = random.random()
if coin < epsilon:
return random.randint(0, 1);
else:
return out.argmax().item()
학습
1
2
3
4
5
6
7
8
9
10
11
12
13
def train(q, q_target, memory, optimizer):
for i in range(10):
s, a, r, s_prime, done_mask = memory.sample(batch_size)
q_out = q(s)
q_a = q_out.gather(1, a)
max_q_prime = q_target(s_prime).max(1)[0].unsqueeze(1)
target = r + gamma * max_q_prime * done_mask
loss = F.smooth_l1_loss(q_a, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
메인 함수
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def main():
env = gym.make('CartPole-v1')
q = Qnet()
q_target = Qnet()
q_target.load_state_dict(q.state_dict())
memory = ReplayBuffer()
best_q = (0, q.state_dict())
print_interval = 20
score = 0.0
optimizer = optim.Adam(q.parameters(), lr=learning_rate)
for n_epi in range(10000):
epsilon = max(0.01, 0.08 - 0.01 * (n_epi / 200))
s = env.reset()
done = False
score = 0.0
while not done:
a = q.sample_action(torch.from_numpy(s).float(), epsilon)
s_prime, r, done, info = env.step(a)
done_mask = 0.0 if done else 1.0
memory.put((s, a, r / 100.0, s_prime, done_mask))
s = s_prime
score += r
if memory.size() > 2000:
train(q, q_target, memory, optimizer)
if score > best_q[0]:
best_q = (score, q.state_dict())
if n_epi % print_interval == 0 and n_epi != 0:
q_target.load_state_dict(q.state_dict())
print("n_episode: {}, score: {:.1f}, n_buffer: {}, eps: {:.1f}%".format(n_epi, score, memory.size(), epsilon * 100))
env.close()
torch.save(q.state_dict(), "./Qnet_final.pt")
torch.save(best_q[1], "./Qnet_best.pt")
main()
결과
This post is licensed under CC BY 4.0 by the author.